
3、 已知
已知 、
、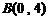 ,从点
,从点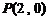 射出的光线经直线
射出的光线经直线 反向后再射到直线
反向后再射到直线 上,最后经直线
上,最后经直线 反射后又回到
反射后又回到 点,则光线所经过的路程是 .
点,则光线所经过的路程是 .
2、过定点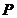 (1,2)的直线在
(1,2)的直线在 正半轴上的截距分别为
正半轴上的截距分别为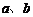 ,则4
,则4 的最小值为 .。
的最小值为 .。
1、设直线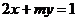 的倾斜角为
的倾斜角为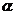 ,若
,若 ,则角
,则角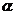 的取值范围是
。
的取值范围是
。
6.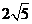
三 范例剖析
例1 (2006年上海春季卷)已知直线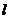 过点
过点 ,且与
,且与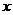 轴、
轴、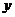 轴的正半轴分别交于
轴的正半轴分别交于 、
、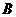 两点,
两点, 为坐标原点,则△OAB面积的最小值为 .
为坐标原点,则△OAB面积的最小值为 .
变式:已知射线 和点
和点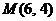 ,在射线
,在射线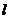 上求一点
上求一点 ,使直线
,使直线 与
与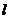 及
及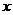 轴围成的三角形面积
轴围成的三角形面积 最小.
最小.
例2 如图,在平面直角坐标系xOy中,平行于x轴且过点A(3,2)的入射光线l1被直线l:y=x反射.反射光线l2交y轴于B点,圆C过点A且与l1, l2都相切.
(1)求l2所在直线的方程和圆C的方程;(10分)
(2)设P,Q分别是直线l和圆C上的动点,求PB+PQ的最小值及此时点P的坐标.(6分)

辨析:已知点A(-1,1)和圆C: ,一束光线从点A出发,经x轴反射后与圆C相切,求(1)光线从点A到切点的路程;(2)入射光线与反射光线所在直线的斜率。
,一束光线从点A出发,经x轴反射后与圆C相切,求(1)光线从点A到切点的路程;(2)入射光线与反射光线所在直线的斜率。
例3 已知圆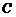 :
: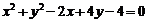 ,一条斜率等于1的直线
,一条斜率等于1的直线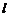 与圆
与圆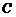 交于
交于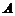 、
、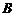 两点.(Ⅰ)求弦
两点.(Ⅰ)求弦 最长时直线
最长时直线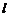 的方程;(Ⅱ)求
的方程;(Ⅱ)求 面积最大时直线
面积最大时直线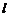 的方程;
的方程;
辨析:已知圆 ,直线
,直线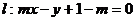 .
.
(1)求证:不论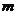 取什么实数,直线
取什么实数,直线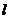 与圆
与圆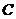 恒交于两点;
恒交于两点;
(2)求直线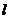 被圆
被圆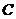 截得的弦长最小时
截得的弦长最小时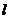 的方程.
的方程.
四 巩固训练
6、已知定点  (3,1),在直线
(3,1),在直线  和
和  上分别求点
上分别求点 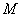 和点
和点 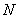 ,使
,使  的周长最短,其最短周长是 .
的周长最短,其最短周长是 .
二 感悟解答
1解:设直线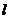 的倾斜角为
的倾斜角为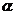 ,则直线
,则直线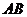 的倾斜角为
的倾斜角为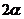 ,依题意有
,依题意有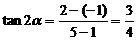 ,∴
,∴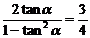 ,∴
,∴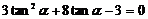 ,∴
,∴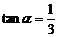 或
或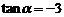 .由
.由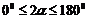 ,得
,得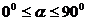 ,∴
,∴ ,∴
,∴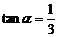 ,∴直线
,∴直线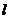 的斜率为
的斜率为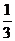 .
.
点评:此题主要是要求学生弄清倾斜角和斜率的关系;
变式: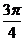 ,
,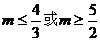
2答: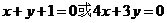
变题答案:设直线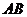 的方程为
的方程为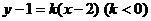 ,
,
则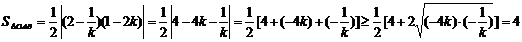 ,当且仅当
,当且仅当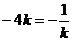 即
即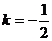 时取等号,∴当
时取等号,∴当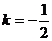 时,
时,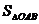 有最小值4.
有最小值4.
点评:该题是直线部分常考题型,是直线和不等式结合的问题。
3答:∵直线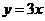 绕原点逆时针旋转
绕原点逆时针旋转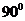 的直线为
的直线为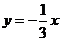 ,又∵将
,又∵将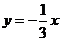 向右平移1个单位得
向右平移1个单位得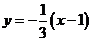 ,即
,即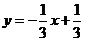
点评:此题重点考察互相垂直的直线关系,以及直线平移问题;
4答:
点评:该题主要是借助数形结合思想解题的
5解:由题意知,点A、B在直线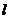 的同一侧.由平面几何性质可知,先作出点
的同一侧.由平面几何性质可知,先作出点 关于直线
关于直线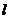 的对称点
的对称点 ,然后连结
,然后连结 ,则直线
,则直线 与
与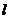 的交点P为所求.事实上,设点
的交点P为所求.事实上,设点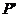 是
是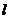 上异于P的点,则
上异于P的点,则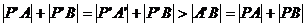 .
.
设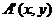 ,则
,则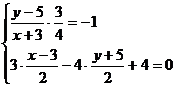 ,解得
,解得 ,∴
,∴ ,∴直线
,∴直线 的方程为
的方程为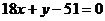 .由
.由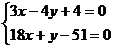 ,解得
,解得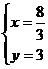 ,∴
,∴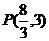 .
.
点评:考查对称问题。
5、已知点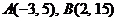 ,在直线
,在直线 上求一点P,使
上求一点P,使 最小。
最小。
4、若三条直线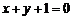 ,
,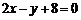 和
和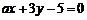 共有三个不同的交点,则
共有三个不同的交点,则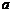 满足的条件
。
满足的条件
。
考点5、两点间的距离、点到直线的距离
3、(08四川卷)直线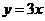 绕原点逆时针旋转
绕原点逆时针旋转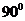 ,再向右平移1个单位,所得到的直线为
。
,再向右平移1个单位,所得到的直线为
。
考点4、两条直线的交点
2、经过点 且在两坐标轴上的截距相等的直线方程是______________________.
且在两坐标轴上的截距相等的直线方程是______________________.
变式题:已知直线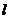 过点
过点 ,且与
,且与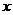 轴、
轴、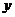 轴的正半轴分别交于
轴的正半轴分别交于 、
、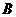 两点,
两点,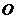 为坐标原点,则△OAB面积的最小值为 .
为坐标原点,则△OAB面积的最小值为 .
考点3、直线的平行关系与垂直关系
1、已知点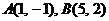 ,直线
,直线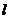 的倾斜角是直线
的倾斜角是直线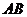 的倾斜角的一半,求直线
的倾斜角的一半,求直线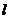 的斜率。
的斜率。
变式: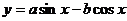 的一条对称轴为
的一条对称轴为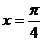 ,则直线
,则直线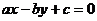 的倾斜角为_____________.
的倾斜角为_____________.
若直线 与线段AB有交点,其中A(-2,3),B(3,2),则实数
与线段AB有交点,其中A(-2,3),B(3,2),则实数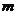 的取值范围为_______________________________.
的取值范围为_______________________________.
考点2、直线方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com