
 ,
, ,……,
,……, 的类型”,得4分,证明结论得5分,共9分.
的类型”,得4分,证明结论得5分,共9分.
如对(2)中的问题有所创新,如:“对于任意给定的正整数 ,判断数列
,判断数列
(3)(理)可以从多个方面加以推广.对一般的以 为首项,
为首项, 为公差的等差数列,
为公差的等差数列,
如照抄(2)中的问题(即三项之和)得3分,证明结论得4分,共得7分;
如对(2)中的问题有所改变,如改为四项之和,得4分,证明得4分,共8分;
∴数列 ,
, ,
, ,…,
,…, 是等差数列……(5分)
是等差数列……(5分)
 ,∴
,∴  (常数)
(常数)
(2)当 为正整数时,
为正整数时,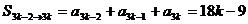
∴ 数列 是等差数列,其通项公式是
是等差数列,其通项公式是 (
( 为正整数)……(4分)
为正整数)……(4分)
∵  是递增数列,∴
是递增数列,∴  ,
, ,
, ……(3分)
……(3分)
(1)解方程 得
得 ,
, ……(1分)
……(1分)
(3)对一般的首项为 ,公差为
,公差为 的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
的等差数列,提出与(2)类似的问题,你可以得到怎样的结论,证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com