所以f(n)= 的最小值只可能在n=2或n=3处取到，

当时，>0，所以，在内单调递增．…………………………………………………………………………2分

所以当时，<0，所以，在内单调递减；

由，

解法三：(Ⅰ)因为f(n)= ,设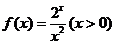

所以S =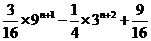

所以2S =(3 ⁿ-1)(1+3+3²+…+3 ^n-1)+(9 ⁿ -1),

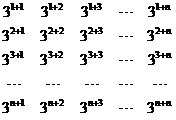
记第一行的和为S₁，那么2S一(3²+3⁴+3⁶+…+3²ⁿ)=S₁(1+3+3²+…+3^n-1).

记数列{3ⁿ}的所有可能的乘积(1≤i≤j≤n)的和为S，将这个“上三角形”表绕“对角线”对称地填在“下三角形”中，得到正方形数表：