7.解：(1)设该镇通过x年达到小康水平，根据题意得2+0.6x=5

解得x=5

(2)设第x年的年国民生产总值为2×4=8亿元，

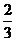∴x²+x+5=8　 　解得x₁=3　 x₂=－9(不合题意舍去)

答：(1)设该镇通过5年达到小康水平，2003年的国民生产总值可在1995年的基础上翻两番。

6.解:对于甲车

∵甲车刹车距离为12米,根据题意,得

12=0.1x+0.01x²

解这个方程得x=30或x=－40(舍去)

即甲车的车速为30千米/时,不超过限速.

对于乙车:

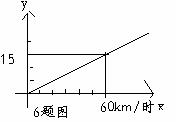
由图像知,其关系是一个正比例函数,

设此函数为S_乙=kx

∵经过点(60,15 ),

∴15=60k

∴k=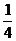

即此函数解析式为S_乙=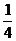x

根据题意得10<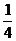x<12

∴40<x<48

∴乙车超过限速40千米/时的规定,

∴就速度方面相碰的原因在乙车超速行驶.

5.解:设拱桥到警戒线的距离为m.

∵抛物线顶点在(0,0),对称轴为y轴,

∴设此抛物线解析式为y=ax².

根据题意此抛物线经过点C的坐标为(－5,－m),

点A的坐标为(－10,－m－3).

∴

∴

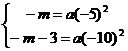
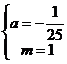
(1)抛物线解析式为y=-x².

(2)∵洪水到来时,水位以每小时0.2米的速度上升,

∴从警戒线开始再持续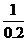=5(小时)到拱桥顶.

4．解：(1)依题意得

y=10000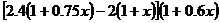

=10000(0.4－0.2x)(1+0.6x)

=－1200x²+400x+4000.

(2)依题意得;4028=－1200x²+400x+4000.

即300x²－100x+7=0 ∴x₁=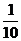 x₂=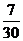

①当x₁=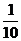时，销售量W₁=10000(1+0.6×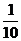)=10600(辆)

②当x₂=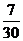时　 销售量W₂=10000(1+0.6×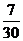)=11400(辆)

答;当每辆车的成本增长率为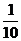时,该厂2001年销售10600辆汽车可得利润4028万元.

当每辆车的成本增长率为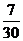时, 该厂2001年销售11400辆汽车长方利润仍然为4028万元.

另解:2001年的成本价为2(1+x)

2001年的出厂价为2.4(1+0.75x)

2001年每辆车的利润为2.4(1+0.75x)－2(1+x)=0.4－0.2x

2001年的年利润为y=10000(0.4－0.2x)(1+0.6x)

销售量的计算方法参照第一种解答。

2． 解：(1)3月份出售这种蔬菜每千克的收益为1元。

(2)设甲图中图像的函数关系式为y_甲=kx+b,

图乙中图像的函数关系式为y_乙=a(x+m)²+n,

每千克收益为y元，由图象知：点(3，5)，(6，3)在y_甲=kx+b上，

∴5=3k+b, 解得，k=－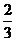

　　 3=6k+b　　　　　 b=7

∴y_甲=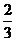－x+7.

抛物线y_乙= a(x+m)²+n的顶点坐标为(6，1)，又过点(3，4)

∴y_乙= a(x－6)²+1

4= a(3－6)²+1，a=。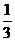

y_乙= 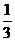(x－6)²+1

∴y= y_甲－y_乙=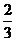－x+7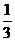－(x－6)²－1

y=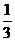－(x－5)²+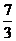

∴当x=5时，y值最大。

答：5月份出售这种蔬菜，每千克收益最大。

2。解；(1)若销售单价为x元，则每千克降低(70－x)元，日均多售出2(70－x)千克，日均销售量为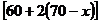千克，每千克获利为(x－30)元

依题意得：

y=(x－3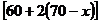0)－500

=－2x²+260x－6500(30≤x≤70)

(2)y=－2(x²－130x)－6500

=－2(x－65)²+1950

顶点坐标为(65，1950)

(图略)

经观察可知，当单价定为65元时，日均获利最多是1950元

(3)当日均获利最多时，单价为65元

日均销售60+2(70－65)=70千克

那么获总利为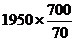=195000元

当销售单价最高时单价为70元，日均销售60千克

将这种化工原料全部售完需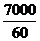≈117天

那么获总利为(70－30)×7000－117×500=221500元

因为221500>195000,且221500－195000=26500元

所以，销售单价最高时获总利较多，且多获利26500元。

1． 解(1)；根据题意得

1750=Px－R,

(17－2x)x－(500+30x)=1750,

整理得x²－70x+1125=0,

(x－25)(x－45)=0,

∴x₁=25,x₂=45(不合题意，舍去)，

由题已知，利润为，

Px－R=－2x²+140x－500

=－2(x²－70x+1125)

=－2

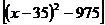
=－2(x－35)²+1950

∴当x=35时，最大利润为1950。

答(1)当日产量为25只时，利润为1950。

(2)当日产量为35只时，最大利润为1950。

7.改革开放以来，某镇通过多种途径发展地方经济，1995年该镇年国民生产总值为2亿元，根据测算，该镇国民生产总产值为5亿元时，可达到小康水平。

(1)　　　 若从1996年开始，改镇国民生产总值每年比上一年增加0.6亿元,该镇通过几年可达到小康水平?

(2)　　　 设以2001年为第一年,该镇第x年的国民生产总值为y亿元，y与x之间的关系是y=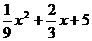(x≥0)该镇那一年的国民生产总值可在1995年的基础上翻两番(即达到1995年的年国民生产总值的4倍)？

答案

6．汽车在行驶中，由于惯力作用，刹车后还要向前滑行一段距离才能停住，我们称这段距离为“刹车距离”，刹车距离是分析事故的一个重要因素，在一个限速40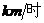乙内的弯道上，甲、乙两车相向而行，发现情况不对，同时刹车，但还是相碰了，事后现场测量甲车的刹车距离为12m，乙车的刹车距离超过10m，但小于20m，查有关资料知，甲种车的刹车距离S_甲(m)与车速x(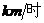)之间有下列关系，S_甲=0.1x+0.01x²,乙种车的刹车距离S_乙(m)与车速x(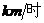)的关系如下图表示，请你就两车的速度方面分析相碰的原因。

.

4. 2000年度东风公司神鹰汽车改装厂开发出A型农用车，其成本价为每辆2万元，出厂价为每辆2.4万元,年销售价为10000辆,2001年为了支援西部大开发的生态农业建设,该厂抓住机遇,发展企业,全面提高A型农用车的科技含量,每辆农用车的成本价增长率为x，出厂增长率为0.75x，预测年销售增长率为0.6x(年利润=(出厂价－成本价)×年销售量)

(1)　　　 求2001年度该厂销售A型农用车的年利润y(万元)与x之间的函数关系。

(2)　　　 该厂要是2001年度销售A型农用车的年利润达到4028万元，该年度A型农用车的年销售量应该是多少辆？

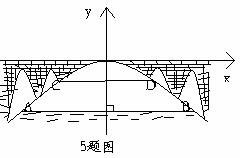
5如图有一座抛物线形拱桥，桥下面在正常水位是AB宽20m，水位上升3m就达到警戒线CD，这是水面宽度为10m。(1)在如图的坐标系中求抛物线的解析式。

(2)若洪水到来时，水位以每小时0.2m的速度上升，从警戒线开始，再持续多少小时才能到拱桥顶？