
14.设集合M={x|x2-mx+6=0},则满足M∩{1,2,3,6}=M的集合M为 ;m的取值范围为 .
8.已知集合M有3个真子集,集合N有7个真子集,那么M∪N的元素个数为( )
A.有5个元素 B.至多有5个元素 C.至少有5个元素 D.元素个数不能确定
9. 若不等式f (x)≥0的解集是F, 不等式g(x)<0的解集是G,则不等式组 的解集是
A B C F∪G D F∩G
10. a>0, b>0, 不等式a> >-b的解集为( )
A - <x<0或0<x< B x<- 或x> C - <x<0或0<x< D - <x<
11. 不等式ax2+ax+(a-1)<0的解集是全体实数,则a的取值范围是( )
A (-∞, 0) B (-∞, 0)∪( ,+∞) C (-∞, 0) D (-∞, 0)∪[ ,+∞]
12. 不等式组 与不等式(x-2)(x-5)≤0同解,则a的取值范围是( )
A a>5 B a<2 C a≤5 D a≤2
二.填空题
13.设全集为 ,用集合A、B、C的交、并、补集符号表图中的阴影部分。
(1) (2)
(3)
4.设集合M= ,则 ( )
A.M =N B. N M C.M N D. N
5. 设全集U={(x,y) },集合M={(x,y },N={(x,y) },那么(CUM) (CUN)等于( )
(A){(2,-2)} (B){(-2,2)} (C) (D)(CUN)
6. 若x=a是不等式组 的解,则P(a+2, a-2)在( )
A 第一象限 B 第二象限 C 第三象限 D 第四象限
7. 不等式(1+x)(1- )>0的解集是( )
A. B. C. D.
2.一元二次不等式x2-7x+12<0, -2x2+x-5>0, x2+2>-2x的解集分别是M、N、P,则有( )
A N M P B M N P C N P M D M P N
3.解不等式ax2+bx+2>0得到解集{x|- <x< },那么a+b的值等于( )
A 10 B -10 C 14 D -14
1.下列八个关系式①{0}= ② =0 ③ = { } ④ { } ⑤{0} ⑥0 ⑦ {0} ⑧ { }其中正确的个数( )
(A)4 (B)5 (C)6 (D)7
21.[解答](Ⅰ)令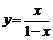 ,解得
,解得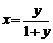 ,由
,由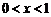 ,解得
,解得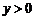 ,
,
∴函数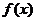 的反函数
的反函数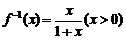 ,
,
则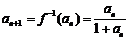 ,得
,得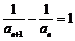 .
.
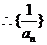 是以2为首项,l为公差的等差数列,故
是以2为首项,l为公差的等差数列,故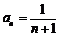 .
.
(Ⅱ)∵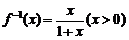 ,∴
,∴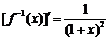 ,
,
∴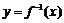 在点
在点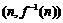 处的切线方程为
处的切线方程为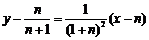 ,
,
令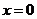 ,
得
,
得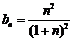 ,
,
∴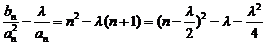 ,
,
∵仅当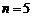 时取得最小值,∴
时取得最小值,∴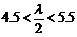 ,解之
,解之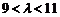 ,
,
∴ 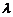 的取值范围为
的取值范围为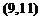 .
.
(Ⅲ)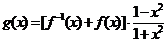
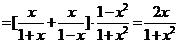 ,
,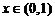 .
.
则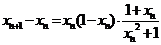 ,
,
因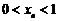 ,则
,则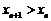 ,显然
,显然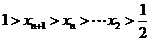 .
.
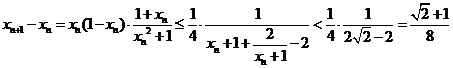 ·
·
∴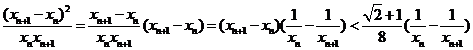
∴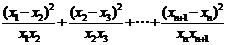
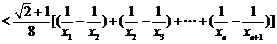
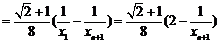
∵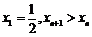 ,∴
,∴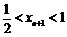 ,
,
∴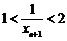 ,∴
,∴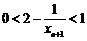
∴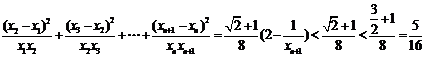 .
.
21.(本小题满分14分)
已知函数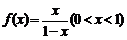 的反函数为
的反函数为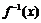 ,数列
,数列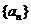 和
和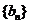 满足:
满足: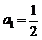 ,
,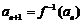 ,函数
,函数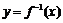 的图象在点
的图象在点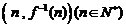 处的切线在
处的切线在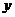 轴上的截距为
轴上的截距为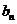 .
.
(Ⅰ)求数列{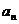 }的通项公式;
}的通项公式;
(Ⅱ)若数列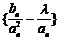 的项仅
的项仅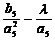 最小,求
最小,求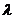 的取值范围;
的取值范围;
(Ⅲ)令函数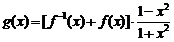 ,
,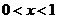 ,数列
,数列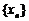 满足:
满足: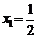 ,
,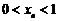 ,且
,且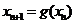 ,其中
,其中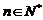 .证明:
.证明: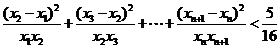 .
.
20.[解答](Ⅰ)分别以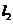 、
、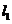 为
为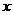 轴,
轴,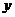 轴建立如图坐标系.据题意得
轴建立如图坐标系.据题意得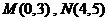 ,
,
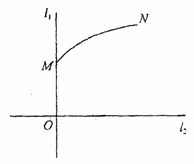
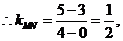
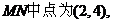
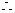 线段
线段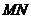 的垂直平分线方程为:
的垂直平分线方程为: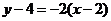 ),
),
故圆心A的坐标为(4,0),
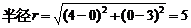 ,
,
∴弧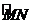 的方程:
的方程: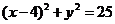 (0≤x≤4,y≥3)
(0≤x≤4,y≥3)
(Ⅱ)设校址选在B(a,0)(a>4),
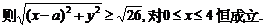
整理得: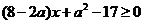 ,对0≤x≤4恒成立(﹡)
,对0≤x≤4恒成立(﹡)
令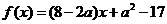
∵a>4 ∴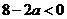 ∴
∴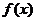 在[0,4]上为减函数
在[0,4]上为减函数
∴要使(﹡)恒成立,当且仅当
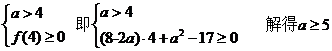 ,
,
即校址选在距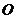 最近5km的地方.
最近5km的地方.
20.(本小题满分13分)
如图,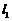 、
、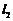 是通过某城市开发区中心
是通过某城市开发区中心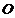 的两条南北和东西走向的街道,连接
的两条南北和东西走向的街道,连接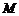 、
、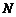 两地之间的铁路线是圆心在
两地之间的铁路线是圆心在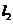 上的一段圆弧.若点
上的一段圆弧.若点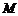 在点
在点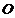 正北方向,且
正北方向,且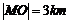 ,点
,点 到
到 、
、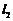 的距离分别为
的距离分别为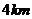 和
和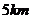 .
.
(Ⅰ)建立适当坐标系,求铁路线所在圆弧的方程;
(Ⅱ)若该城市的某中学拟在点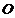 正东方向选址建分校,考虑环境问题,要求校址到点
正东方向选址建分校,考虑环境问题,要求校址到点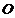 的距离大于
的距离大于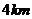 ,并且铁路线上任意一点到校址的距离不能少于
,并且铁路线上任意一点到校址的距离不能少于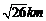 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
19. [解答] (Ⅰ)设点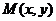 ,由
,由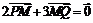 得
得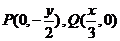 ,
,
由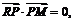 得
得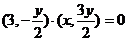 即
即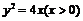 .
.
(Ⅱ)由题意可知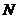 为抛物线
为抛物线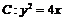 的焦点,且
的焦点,且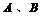 为过焦点
为过焦点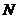 的直线与抛物线
的直线与抛物线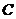 的两个交点.
的两个交点.
当直线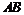 斜率不存在时,得A(1,2),B(1,-2),|AB|
斜率不存在时,得A(1,2),B(1,-2),|AB|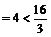 ,不合题意;
,不合题意;
当直线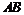 斜率存在且不为0时,设
斜率存在且不为0时,设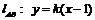 ,代入
,代入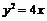 得
得
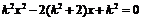
则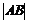
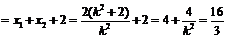 ,解得
,解得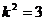 ,
,
代入原方程得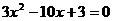 ,得
,得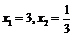 或
或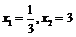 ,
,
由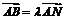 ,得
,得 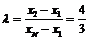 或4.
或4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com