
6.已知 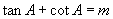 ,则
,则
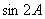 等于( )
A.
等于( )
A.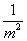 B.
B.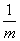 C.
C.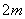 D.
D. 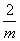
5. 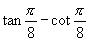 的值为( )
A.-2 B.-1 C.2 D.0
的值为( )
A.-2 B.-1 C.2 D.0
4.若 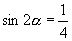 ,且
,且
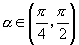 ,则
,则
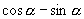 的值是( )
A.
的值是( )
A.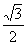 B.
B.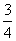 C.
C.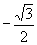 D.
D. 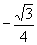
3.已知 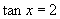 ,则
,则
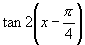 等于( )
A.
等于( )
A.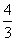 B.
B.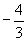 C.
C.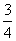 D.
D. 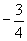
2.已知  是第三象限角,且
是第三象限角,且
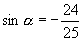 ,则
,则
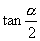 等于( )
A.
等于( )
A. 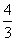 B.
B. 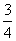 C.
C.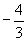 D.
D. 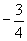
(五)板书设计
|
二倍角的正弦、余弦、正切 1.复述二倍角公式 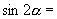 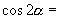 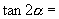 2.由 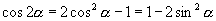 ,
推出半角公式 ,
推出半角公式 |
1.课本例 2.例1 3.例2 4.例3 |
练习(投影) 总结提炼 |
典型例题
例1.求 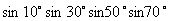 的值.
分析:逆用二倍角公式,或构造对偶式列方程求解.
解:解法一:
的值.
分析:逆用二倍角公式,或构造对偶式列方程求解.
解:解法一:
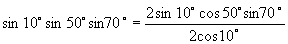
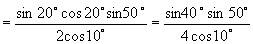
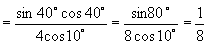 ,
∴
,
∴ 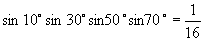 .
解法二:
原式
.
解法二:
原式 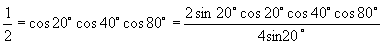
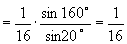 .
解法三:令
.
解法三:令  ,
,
 .
则
.
则 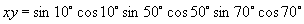
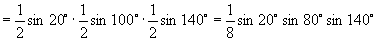
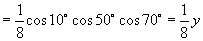 .
∵
.
∵ 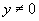 ,∴
,∴ 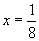 .
从而有
.
从而有 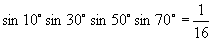 .
小结:对于本题,如若简单地从形式上看,为利用二倍角正弦公式而同乘同除式子
.
小结:对于本题,如若简单地从形式上看,为利用二倍角正弦公式而同乘同除式子
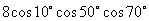 ;或原式
;或原式
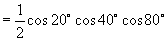 后,简单地应用二倍角的余弦公式都将无益于问题的解决,反而会陷入思维的简单循环之中.因此,当我们面对一个较为陌生的问题时,应认真分析问题的特征,积极地进行联想化归,切实做到缜密稳妥地设计解题思路.
(1)有些数学问题,可根据其本身特点,相应地构设与其相同“匹配”的另一整体,然后由其“相依而伴”的关系进行求解.如解法三,这种解题方法称为积式配对.
(2)角度成等比(公比为2)的同名弦函数的乘积通常可按解法一、二来求解.
后,简单地应用二倍角的余弦公式都将无益于问题的解决,反而会陷入思维的简单循环之中.因此,当我们面对一个较为陌生的问题时,应认真分析问题的特征,积极地进行联想化归,切实做到缜密稳妥地设计解题思路.
(1)有些数学问题,可根据其本身特点,相应地构设与其相同“匹配”的另一整体,然后由其“相依而伴”的关系进行求解.如解法三,这种解题方法称为积式配对.
(2)角度成等比(公比为2)的同名弦函数的乘积通常可按解法一、二来求解.
例2.设
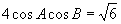 ,
,
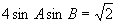 ,求
,求
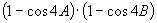 的值.
分析:观察问题的角度状况,从已知条件和被求式的角度差异来看,一方面应将条件中的角度变换为
的值.
分析:观察问题的角度状况,从已知条件和被求式的角度差异来看,一方面应将条件中的角度变换为 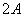 、
、
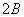 ,另一方面应将被求式中的角度
,另一方面应将被求式中的角度
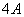 、
、
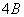 变换为
变换为
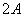 、
、
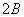 .要实现上述想法只需将两已知条件相乘,将被求式利用升幂公式即可办到.解:两已知条件相乘,可得
.要实现上述想法只需将两已知条件相乘,将被求式利用升幂公式即可办到.解:两已知条件相乘,可得
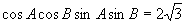 ,
化简为
,
化简为 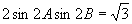 ,
∴
,
∴ 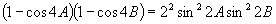
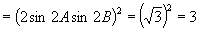 .
小结:根据问题的具体特点,从变换已知条件和被求式的角度入手,进行双向变换实现角度的统一,然后利用代入法将已知条件代入被求式,从而达到求值的目的,这就是解答本题的脉络.
.
小结:根据问题的具体特点,从变换已知条件和被求式的角度入手,进行双向变换实现角度的统一,然后利用代入法将已知条件代入被求式,从而达到求值的目的,这就是解答本题的脉络.
例3.已知
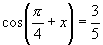 ,
,
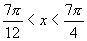 .求
.求
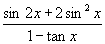 的值.
分析:若对结论“切化弦”后再化简不难发现,只需求出
的值.
分析:若对结论“切化弦”后再化简不难发现,只需求出
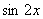 和
和
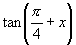 的值即可,注意到
的值即可,注意到
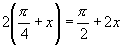 ,就可以发现求解的途径了.
解:∵
,就可以发现求解的途径了.
解:∵ 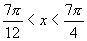 ,∴
,∴ 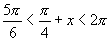 .
又∵
.
又∵ 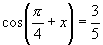 ,∴
,∴ 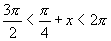 ,
∴
,
∴ 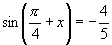 ,
,
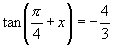 .
又∵
.
又∵ 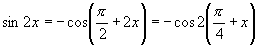
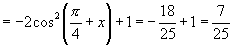 ,
∴原式
,
∴原式 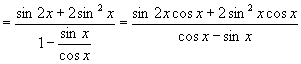
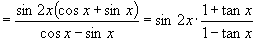
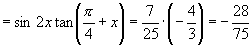 .
小结:(1)本题也可以由
.
小结:(1)本题也可以由 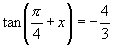 得
得
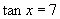 ,再将要求解的三角式化为用
,再将要求解的三角式化为用
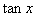 表示的形式.
(2)本题解法中巧妙地利用了“角的变换”
表示的形式.
(2)本题解法中巧妙地利用了“角的变换” 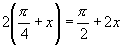 ,使求解过程不致于繁杂.
(3)若不注意
,使求解过程不致于繁杂.
(3)若不注意  的范围,就会导致由
的范围,就会导致由
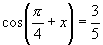 求出
求出
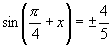 而不知取舍.
而不知取舍.
例4.设
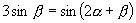 ,
,
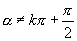 ,
,
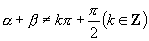 .求证:
.求证:
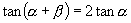 .
分析:条件恒等式的证明,要注意观察条件和结论之间的差异.主要是看角,看函数的名称、次数.对于本题,从角的差异入手,将角变形为
.
分析:条件恒等式的证明,要注意观察条件和结论之间的差异.主要是看角,看函数的名称、次数.对于本题,从角的差异入手,将角变形为 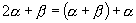 ,
,
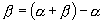 ,从已知条件变形入手,可证得结论.
证明:由
,从已知条件变形入手,可证得结论.
证明:由 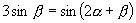 ,得
,得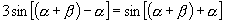 ,
,
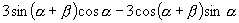
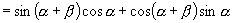 整理,得
整理,得 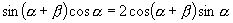 .
为
.
为 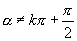 ,
,
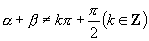 ,将上式两边同除以
,将上式两边同除以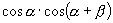 ,得
,得
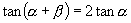 .
小结:证明条件恒等式,一般有两种方法,即推出法与代入法,无论使用哪一种思路都要盯住目标,据果变形.若用推出法,则应盯住欲证等式的左、右两边,根据它们的状况(一般要看角、函数名称、次数),采取恰当的措施来对条件等式进行变形,直到目标.若用代入法,就要盯住作为目标的被证等式的一边,根据它对欲证等式的另一边及条件进行变形,先创造机会,然后代入条件,最终推出目标.
.
小结:证明条件恒等式,一般有两种方法,即推出法与代入法,无论使用哪一种思路都要盯住目标,据果变形.若用推出法,则应盯住欲证等式的左、右两边,根据它们的状况(一般要看角、函数名称、次数),采取恰当的措施来对条件等式进行变形,直到目标.若用代入法,就要盯住作为目标的被证等式的一边,根据它对欲证等式的另一边及条件进行变形,先创造机会,然后代入条件,最终推出目标.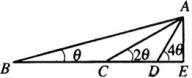
例5.如图,在某点
 处测得建筑物
处测得建筑物
 的顶端
的顶端
 的仰角为
的仰角为
 ,沿
,沿
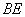 方向前进30米至点
方向前进30米至点 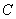 处测得顶端
处测得顶端
 的仰角为
的仰角为
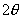 ,再继续前进
,再继续前进
 米至
米至
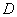 点,测得顶端仰角为
点,测得顶端仰角为
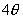 ,求
,求
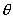 的大小和建筑物
的大小和建筑物
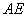 的高.
分析:根据题意结合图形观察给出各数据间的关系,将题目数学化,抽象为纯数学问题.
解:由已知,
的高.
分析:根据题意结合图形观察给出各数据间的关系,将题目数学化,抽象为纯数学问题.
解:由已知, 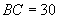 米,
米,
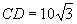 米
在
米
在 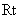 △
△ 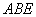 中,
中,
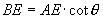 ,
在
,
在 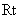 △
△ 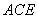 中,
中,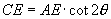 ∴
∴ 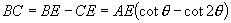 ,同理可得:
,同理可得:
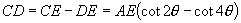 于是:
于是: 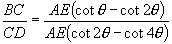 即
即
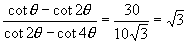 而
而 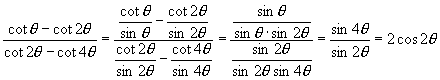 ∴
∴ 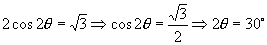
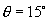 ,
∴
,
∴ 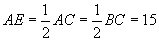 米
于是:
米
于是: 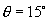 ,建筑物高为15米.
小结:这是一个三角函数在测量方面的应用问题,在解决过程中运用了几何知识和方程的思想,但三角式的化简起到了关键作用.
,建筑物高为15米.
小结:这是一个三角函数在测量方面的应用问题,在解决过程中运用了几何知识和方程的思想,但三角式的化简起到了关键作用.
扩展资料
有趣的米勒问题
米勒(Johannes Miiller),德国数学家,曾在莱比锡、维也纳学习天文学和三角学,1468年至1471年在维也纳大学任教授,1471年定居纽伦堡,从事天文学研究,米勒对三角学做出了贡献.大约在1461至1464年间,他写成《论三角》书,书中给出了有关球面三角学的正弦定理、余弦定理、计算了三角函数表,相当精确.他的这些工作使三角学脱离文学而成为一门独立的学科.另外,米勒在研究几何时采用了代数方法,这在当时是别具一格的.
1471年,米勒向诺德尔(Christian Roder)教授提出以下十分有趣的问题:
在地球表面的什么部位,一根垂直的悬杆呈现最长?(即在什么部位,可见角为最大?)
在米勒的家乡哥尼斯堡,这个问题称为雷奇奥莫塔努斯(Reqiomontanus)的极大值问题.该问题本身并不难,然而作为载入世界数学史上的第一个极值问题而引人注目.
下面这个简明解法是罗斯(Ad·Lorsch)给出的.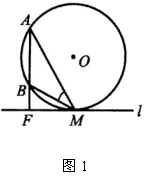 如图1,设
如图1,设  为杆的上端点,
为杆的上端点,
 为杆的下端点.
为杆的下端点.
 垂直于地平面,垂足记为
垂直于地平面,垂足记为
 ,于是线段长
,于是线段长
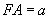 ,
,
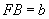 均为已知,以
均为已知,以
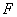 为中心在地球表面上画的圆上的所有对
为中心在地球表面上画的圆上的所有对
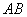 的视角都相等.因此,我们只需过
的视角都相等.因此,我们只需过
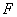 任作一条垂直于
任作一条垂直于
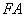 的直线
的直线
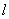 并在这条水平地沿着地球表面的线上找出这样的点
并在这条水平地沿着地球表面的线上找出这样的点
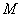 ,使得在这点的可见角
,使得在这点的可见角
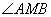 最大.
△
最大.
△ 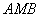 的外接圆
的外接圆
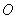 必与
必与
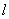 相切干
相切干
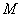 点.事实上,若
点.事实上,若
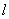 不与圆
不与圆
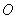 相切,则除
相切,则除
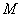 点儿圆
点儿圆
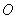 与
与
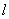 还有另一个公共点
还有另一个公共点
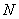 ,而对于线段
,而对于线段
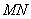 的中点
的中点
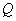 而言,
而言,
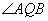 是圆
是圆
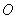 的圆内角,这时,
的圆内角,这时,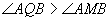 ,这就与
,这就与
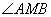 是最大可见角矛盾.
设过
是最大可见角矛盾.
设过 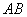 的圆
的圆
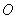 与直线
与直线
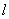 相切于点
相切于点
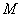 ,则
,则
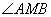 取得最大值.这是因为对
取得最大值.这是因为对
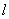 上异于
上异于
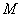 的任一点
的任一点
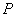 而言,
而言,
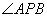 是圆
是圆
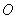 的圆外角,所以
的圆外角,所以
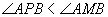 .
.
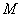 点的位置可以这样来确定,根据切割线定理,
点的位置可以这样来确定,根据切割线定理, 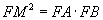 ,即有
,即有
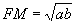 .
从而,我们得出结论:以是杆与地面垂直的垂足为圆心,以是杆两端到地面距离的乘积的算术根为半径,在地球表面上画圆,该圆周上的点对悬杆的视角为最大.
1986年全国高考数学试题理科第五大题其实就是“米勒问题”:
.
从而,我们得出结论:以是杆与地面垂直的垂足为圆心,以是杆两端到地面距离的乘积的算术根为半径,在地球表面上画圆,该圆周上的点对悬杆的视角为最大.
1986年全国高考数学试题理科第五大题其实就是“米勒问题”: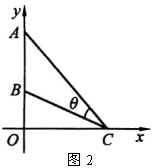
如图2,在平面直角坐标系中,在  轴的正半轴(坐标原点除外)上给定两点
轴的正半轴(坐标原点除外)上给定两点
 ,
,
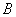 .试在
.试在
 轴的正半轴(坐标原点除外)上求点
轴的正半轴(坐标原点除外)上求点
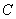 ,使
,使
 取得最大值.
下面,我们运用高中数学知识结出这道高考题的一种简洁解法.
解 如图3,设点
取得最大值.
下面,我们运用高中数学知识结出这道高考题的一种简洁解法.
解 如图3,设点  的坐标为
的坐标为
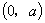 ,点
,点
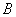 的坐标为
的坐标为
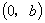 ,
,
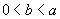 ,
,
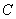 的坐标为
的坐标为
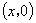 ,
,
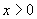 ,并记
,并记
 ,
,
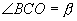 ,
,
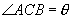 ,则
,则
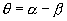 ,且
,且
 .
.
所以 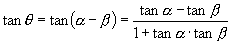
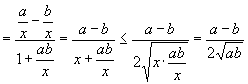 .
因此,当
.
因此,当 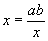 ,即
,即
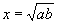 时,
时,
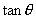 取得最大值
取得最大值
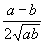 .
因为在
.
因为在 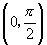 内
内
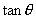 是增函数,所以当
是增函数,所以当
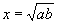 时,
时,
 取得最大值
取得最大值
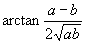 .故所求的
.故所求的
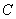 点坐标为
点坐标为
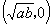 .
更一般的“米勒问题”(解略)是:
在已知直线
.
更一般的“米勒问题”(解略)是:
在已知直线 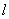 的同侧有
的同侧有
 ,
,
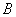 两点,试在
两点,试在
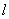 上求一点
上求一点
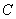 ,使
,使
 最大.
将此问题特殊化,便可得到1984年西安市中学生数学竞赛试题:
在直线
最大.
将此问题特殊化,便可得到1984年西安市中学生数学竞赛试题:
在直线 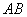 上求点
上求点
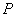 (如图3),使
(如图3),使 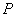 对线段
对线段
 有最大视角,证明你的结论.
有最大视角,证明你的结论.
(原载《数学通讯》2000年第22期,宋庆文)
习题精选
(三)教学过程
1.设置情境
请同学看教材第3页上的一段文字,它叙述的是一个生活中的实际问题:
 “如图1,是一块以点
“如图1,是一块以点 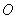 为圆心的半圆形空地,要在这块空地上画出一个内接矩形
为圆心的半圆形空地,要在这块空地上画出一个内接矩形
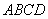 辟为绿地,使其一边
辟为绿地,使其一边
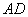 落在半圆的直径上,另两点
落在半圆的直径上,另两点
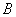 、
、
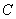 落在半圆的圆周上.已知半圆的半径为
落在半圆的圆周上.已知半圆的半径为
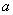 ,如何选择关于点
,如何选择关于点
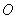 对称的点
对称的点
 、
、
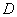 的位置,可以使矩形
的位置,可以使矩形
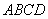 的面积最大?”根据教材提示应用所学的倍角公式,同学们能尝试解答它吗?
2.探索研究
分析:要使矩形
的面积最大?”根据教材提示应用所学的倍角公式,同学们能尝试解答它吗?
2.探索研究
分析:要使矩形 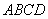 的面积最大,就必须想办法把面积表示出来,不妨利用我们所学的三角知识,从角的方面进行考虑,设
的面积最大,就必须想办法把面积表示出来,不妨利用我们所学的三角知识,从角的方面进行考虑,设
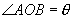 ,则
,则
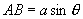 ,
,
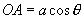 ,所以
,所以
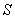 可以用
可以用
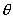 表示.
解:设
表示.
解:设 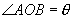 则
则
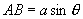
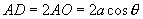
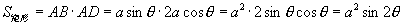 ∵
∵ 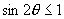 ∴
∴ 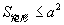 当
当 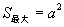 时,
时,
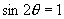 即
即 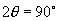 ,
,
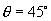 这时
这时 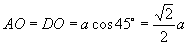 ,
,
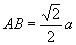 答:点
答:点  、
、
 分别位于点
分别位于点
 的左、右方
的左、右方
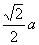 处时
处时
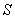 取得最大值
取得最大值
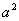 .
变式:把一段半径为
.
变式:把一段半径为 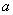 的圆木锯成横截面为矩形的木料,怎样锯法才能使横截面的面积最大?
生:根据上题的结果可知这时圆内接矩形为内接正方形时面积最大.
以上是倍角公式在实际生活中的运用,请同学们观察以下例题,并分析、思考后能否得出证明.
3.例题分析
[例1]求证:
(1)
的圆木锯成横截面为矩形的木料,怎样锯法才能使横截面的面积最大?
生:根据上题的结果可知这时圆内接矩形为内接正方形时面积最大.
以上是倍角公式在实际生活中的运用,请同学们观察以下例题,并分析、思考后能否得出证明.
3.例题分析
[例1]求证:
(1) 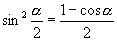 ;(2)
;(2) 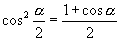 ;
(3)
;
(3)  .
思考,讨论.
我们知道公式
.
思考,讨论.
我们知道公式 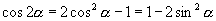 中
中
 是任意的,所以我们可以用
是任意的,所以我们可以用
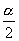 来替换
来替换
 ,这样就得到
,这样就得到
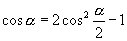
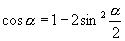 即
即 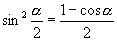
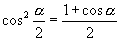
 上面三式左边都是平方形式,当
上面三式左边都是平方形式,当 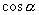 的值已知,
的值已知,
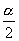 角的终边所在象限已知时,就可以将右边开方,从而求得:
角的终边所在象限已知时,就可以将右边开方,从而求得:
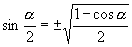
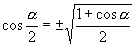 以上两式相除又得:
以上两式相除又得:
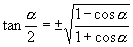 这三个式子称之为半角公式,“±”号的取舍得由
这三个式子称之为半角公式,“±”号的取舍得由 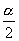 终边所在象限确定.
终边所在象限确定.
[例2]求证:
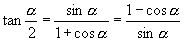 .
分析:从例1引出例2,
.
分析:从例1引出例2, 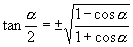 ,右边是同一个三角函数,并且还要附上正负号,而所要证明的式子右边有两个三角函数,不带正负号.故我们不能利用上法,得另想办法.
师:(边叙述边板书)
,右边是同一个三角函数,并且还要附上正负号,而所要证明的式子右边有两个三角函数,不带正负号.故我们不能利用上法,得另想办法.
师:(边叙述边板书)
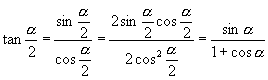
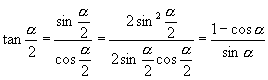 ∴
∴ 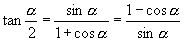 上式不含根号也不必考虑“±”号选取,通常用于化简或证明三角恒等式,同样可作半角公式运用.
上式不含根号也不必考虑“±”号选取,通常用于化简或证明三角恒等式,同样可作半角公式运用.
[例3]已知: 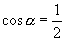 ,求
,求
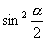 ,
,
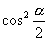 ,
,
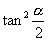 .
解:
.
解: 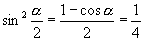
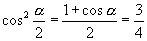
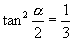 说明:①例1中(1)、(2)两式使用频率极高,正、逆使用都非常普遍.习惯从左到右,常称“扩角降幂公式”,从右到左常谓“缩角升幂公式”,
②半角公式是二倍角公式的另一种表达方式,倍半关系是相对的.
练习(投影)
1.已知:
说明:①例1中(1)、(2)两式使用频率极高,正、逆使用都非常普遍.习惯从左到右,常称“扩角降幂公式”,从右到左常谓“缩角升幂公式”,
②半角公式是二倍角公式的另一种表达方式,倍半关系是相对的.
练习(投影)
1.已知: 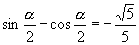 (
(
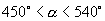 ),
求:(1)
),
求:(1) 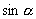 ;(2)
;(2) 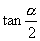 .
2.若
.
2.若 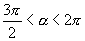 ,求:
,求:
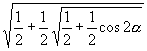 的值.
3.求:
的值.
3.求: 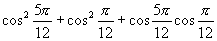 的值.
的值.
参考答案:
解:1.∵ 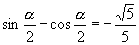 两边平方得
两边平方得 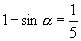 ∴
∴
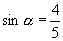 又∵
又∵ 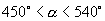 ∴
∴ 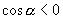 ∴
∴ 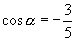 ∴
∴ 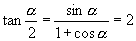 2.∵
2.∵  ∴
∴  原式
原式 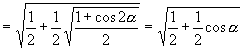
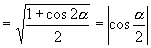
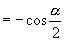 (3)
(3) 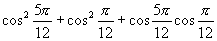
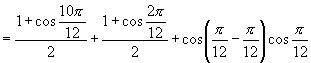

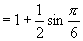
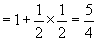 另解:设
另解:设 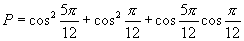 ……………………①
……………………①
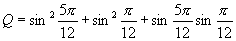 ……………………②
①+②得
……………………②
①+②得 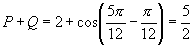 …………………………③
①-②得
…………………………③
①-②得 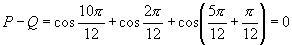 ……④
③+④得
……④
③+④得 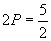 ∴
∴ 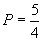 4.总结提炼
(1)本节课我们由倍角公式出发解决了实际应用问题,得出结论“在一个圆的所有内接矩形中,以内接正方形的面积为最大”,另外由倍角公式解答了例1、例2,从而推导出半角公式,公式“±”号的选取决定于
4.总结提炼
(1)本节课我们由倍角公式出发解决了实际应用问题,得出结论“在一个圆的所有内接矩形中,以内接正方形的面积为最大”,另外由倍角公式解答了例1、例2,从而推导出半角公式,公式“±”号的选取决定于 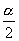 终边所在的象限,例2的应用也很广泛,大家可根据题目的条件选择使用较为方便的形式.
(2)从半角公式可以看出,半角的正弦、余弦、正切公式都可以用单角的余弦来表示.
(3)若给出的
终边所在的象限,例2的应用也很广泛,大家可根据题目的条件选择使用较为方便的形式.
(2)从半角公式可以看出,半角的正弦、余弦、正切公式都可以用单角的余弦来表示.
(3)若给出的  是象限角,则可根据下表决定符号.
是象限角,则可根据下表决定符号.
 的终边 的终边 |
一 |
二 |
三 |
四 |
|
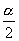 的终边 的终边 |
一或三 |
一或三 |
二或四 |
二或四 |
|
若给出的  是区间角,则先求
是区间角,则先求
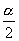 所在区间再确定符号.
若没有给出确定符号的条件,则应在根号前保留“±”号.
所在区间再确定符号.
若没有给出确定符号的条件,则应在根号前保留“±”号.
(二)教学目标 1.应用倍角公式解决本章开头的一个应用问题. 2.活用倍角公式,推求半角公式.
(一)教学具准备 投影仪
(四)板书设计
二倍角公式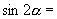 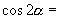 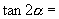 应注意几个问题: |
例1 例2 例3 例4 |
演练反馈 总结提炼 |
教学设计示例(二)
4.7二倍角的正弦、余弦、正切(第二课时)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com