
(三)教学过程
1.设置情境
师:我们已经学习了两角和与差的正弦、余弦、正切公式,请大家回忆一下这组公式的来龙去脉,并请一个同学把这六个公式写在黑板上,
生:
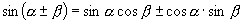
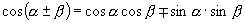
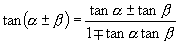 师:很好,对于这些公式大家一方面要从公式的推导上去理解它,另一方面要从公式的结构特点上去记忆,还要注意公式的正用、逆用和变用.今天,我们继续学习二倍角的正弦、余弦和正切公式
2.探索研究
师:请大家想一想,在公式
师:很好,对于这些公式大家一方面要从公式的推导上去理解它,另一方面要从公式的结构特点上去记忆,还要注意公式的正用、逆用和变用.今天,我们继续学习二倍角的正弦、余弦和正切公式
2.探索研究
师:请大家想一想,在公式 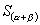 、
、
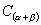 、
、
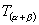 中对
中对
 、
、
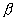 如何合理赋值,才能出现
如何合理赋值,才能出现
 、
、
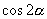 、
、
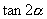 的表达式,并请同学把对应的等式写在黑板上.
生:可在
的表达式,并请同学把对应的等式写在黑板上.
生:可在 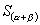 、
、
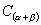 、
、
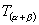 中,令
中,令
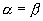 ,就能出现
,就能出现
 、
、
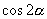 、
、
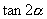 ,对应表达式为:
,对应表达式为:

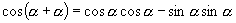
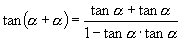 即:
即: 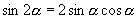
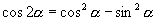
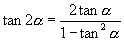 师:很好,看来本节课的主要任务,已经被大家轻松完成了.对于公式
师:很好,看来本节课的主要任务,已经被大家轻松完成了.对于公式 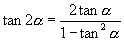 ,我们似乎要注意些什么?大家想一想要关注什么?
生:要使
,我们似乎要注意些什么?大家想一想要关注什么?
生:要使 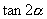 有意义及
有意义及
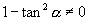 ,
,
 有意义.
师:
有意义.
师: 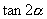 有意义即
有意义即
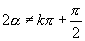 ,
,
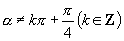 .
.
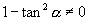 ,即
,即
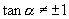 ,也就是
,也就是
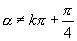 ,可变为
,可变为
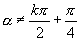 .
要使
.
要使  有意义,则须
有意义,则须
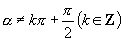 .
综合起来就是
.
综合起来就是 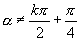 ,且
,且
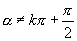 ,
,
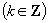 .当
.当
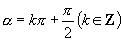 时,虽然
时,虽然
 的值不存在,但
的值不存在,但
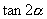 的值是存在的,这时求
的值是存在的,这时求
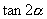 的值可利用诱导公式,即
的值可利用诱导公式,即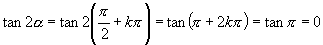 .
师:对于
.
师:对于 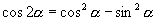 ,还有没有其他的形式?
生:有(板书)
∵
,还有没有其他的形式?
生:有(板书)
∵ 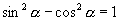 ∴
∴ 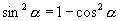 或
或
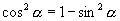 ∴
∴ 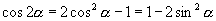 师:(板书三个公式,并告诉学生公式记号分别为
师:(板书三个公式,并告诉学生公式记号分别为 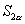 、
、
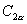 、
、
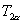 )对二倍角公式大家要注意以下问题.(1)用
)对二倍角公式大家要注意以下问题.(1)用 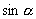 和
和
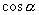 表示
表示
 、
、
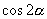 ,用
,用
 表示
表示
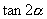 ,即用单角的三角函数表示复角的三角函数.(2)
,即用单角的三角函数表示复角的三角函数.(2) 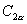 有三种形式,
有三种形式,
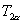 是有条件的.
3.例题分析
[例1]已知
是有条件的.
3.例题分析
[例1]已知 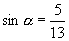 ,
,
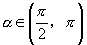 .求
.求
 ,
,
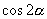 ,
,
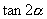 的值.
解:因为
的值.
解:因为 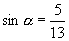 ,
,
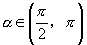 .所以
.所以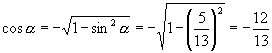 于是
于是 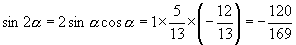
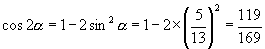
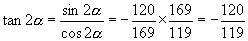 说明:本题也可按下列程序来做,请大家比较方法之优劣.
∵
说明:本题也可按下列程序来做,请大家比较方法之优劣.
∵ 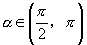 ,
,
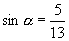 ∴
∴ 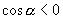 ,且
,且
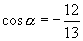 ,
,
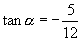
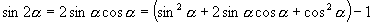
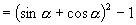
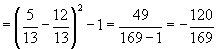
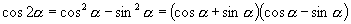
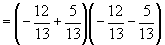
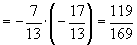
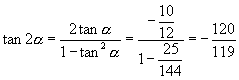
[例2]不查表求值:
(1)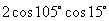 ; (2)
; (2) 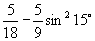 ;
(3)
;
(3)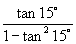 ; (4)
; (4) 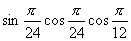 .
解:(1)
.
解:(1) 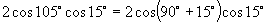
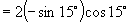
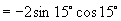
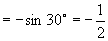
(2) 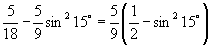
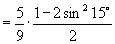

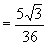
(3)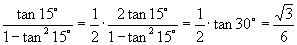 (4)
(4) 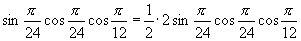
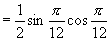
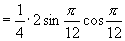
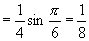 说明:逆用公式的先决条件是认识公式的本质,要善于把表象的东西拿开,正确捕捉公式原形以便合理运用公式.
说明:逆用公式的先决条件是认识公式的本质,要善于把表象的东西拿开,正确捕捉公式原形以便合理运用公式.
[例3] 求证: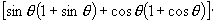
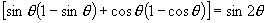 引导学生观察式子两边的结构,提出证题的方向.
生:左边都是单角的三角函数,右边是二倍角.又因左边比右边明显复杂得多,所以应由左边证向右边,注意把单角的三角函数变为二倍角.
师:(板书)
证明:左边
引导学生观察式子两边的结构,提出证题的方向.
生:左边都是单角的三角函数,右边是二倍角.又因左边比右边明显复杂得多,所以应由左边证向右边,注意把单角的三角函数变为二倍角.
师:(板书)
证明:左边 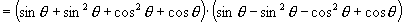
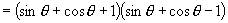
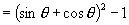
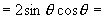 右边
所以原式成立
右边
所以原式成立
[例4]化简: 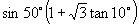 .
师:这道题给我们的感觉是有些无从下手,很难看出有什么公式可以直接使用.两个角
.
师:这道题给我们的感觉是有些无从下手,很难看出有什么公式可以直接使用.两个角 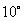 与
与
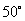 似乎还有一线希望,但由于受函数名称限制难以发挥它的作用,大家都来想想看,有什么办法可以打破这一僵局(请同学们讨论)?
生:在同角三角函数的化简中,如果一个式子有弦、有切,我们可以把切化成弦.
师:好的,我们来尝试(板书)
解:
似乎还有一线希望,但由于受函数名称限制难以发挥它的作用,大家都来想想看,有什么办法可以打破这一僵局(请同学们讨论)?
生:在同角三角函数的化简中,如果一个式子有弦、有切,我们可以把切化成弦.
师:好的,我们来尝试(板书)
解: 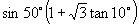
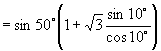
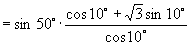
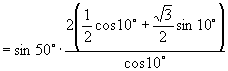
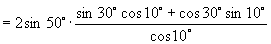
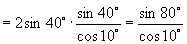
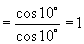 说明:本题在尝试把正切化为弦(正、余弦)后果然获得成功,其实把正切化为弦就是一条重要思想,请同学们切记“遇切、割化弦”这一规律.另外本题的解答过程还反映了逆用和角公式的重要性.希望大家一并记下.
说明:本题在尝试把正切化为弦(正、余弦)后果然获得成功,其实把正切化为弦就是一条重要思想,请同学们切记“遇切、割化弦”这一规律.另外本题的解答过程还反映了逆用和角公式的重要性.希望大家一并记下.
练习(投影)
(1)化简 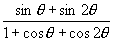 (2)
(2) 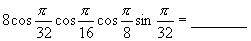 (3)若
(3)若 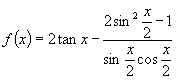 ,则
,则
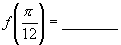 答案:(1)
答案:(1) 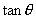 ;(2)
;(2)  ;(3)8
;(3)8
4.总结提炼
(1)在两角和的三角函数公式 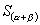 、
、
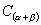 、
、
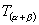 中,当
中,当
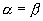 时,就可以得到二倍角的三角函数公式
时,就可以得到二倍角的三角函数公式
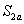 、
、
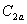 、
、
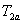 ,说明后者是前者的特例.
(2)
,说明后者是前者的特例.
(2) 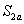 、
、
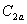 中角
中角
 没有限制条件,而
没有限制条件,而
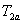 中,只有
中,只有
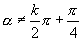 和
和
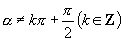 时,才成立.
(3)二倍角公式不仅限于
时,才成立.
(3)二倍角公式不仅限于 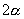 是
是
 的二倍形式,其他如
的二倍形式,其他如
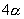 是
是
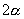 的2倍,
的2倍, 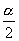 是
是
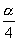 的二倍,
的二倍,
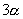 是
是
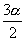 的二倍等等都是适用的,要熟悉这些多种形式的两个角的倍数关系,才能熟练地应用好二倍角公式,这是灵活运用公式的关键.
的二倍等等都是适用的,要熟悉这些多种形式的两个角的倍数关系,才能熟练地应用好二倍角公式,这是灵活运用公式的关键.
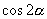 有三种形式
有三种形式
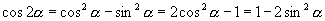 ,要依据条件,灵活选用公式.另外,逆用此公式时,更要注意结构形式.
,要依据条件,灵活选用公式.另外,逆用此公式时,更要注意结构形式.
(二)教学目标
1.掌握 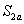 、
、
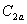 、
、
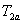 公式的推导,明确
公式的推导,明确
 的取值范围.
2.运用二倍角公式求三角函数值.
的取值范围.
2.运用二倍角公式求三角函数值.
(一)教学具准备 投影仪或多媒体设备
24.化简: 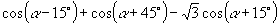 .
.
25.已知在△ 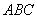 中,
中,
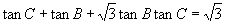 ,又
,又
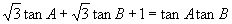 ,试判断△
,试判断△
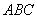 的形状.
的形状.
26.化简: 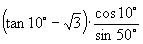 .
.
27.已知: 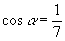 ,
,
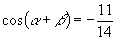 ,求
,求
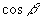 的值.
的值.
28.设  为实数,且点
为实数,且点
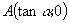 ,
,
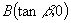 是二次函数
是二次函数
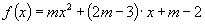 图像上的点,求函数
图像上的点,求函数
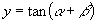 的最小值.
的最小值.
[答案与提示]
1.C 2.B 3.A 4.C 5.B 6.B 7. 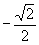 8.
8. 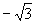 9.
9. 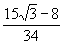 10.
10. 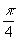 11. ,
11. , 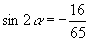 ,
,
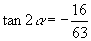 ,提示:
,提示:
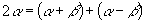 12.-1 13.
12.-1 13. 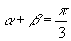 14.
14.  15.提示:
15.提示: 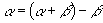 16.D 17.D 18.D 19.
16.D 17.D 18.D 19. 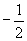 提示:消去角
提示:消去角
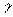 20.
20. 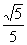 21.-3 22.-6,提
21.-3 22.-6,提
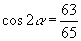 示:
示:
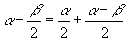 ,
,
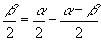 23.-7,提示:
23.-7,提示: 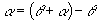 24.0,提示:
24.0,提示: 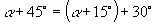 25.顶角为
25.顶角为 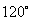 的等腰三角形 26.-2 27.
的等腰三角形 26.-2 27. 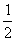 或
或
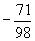 28.
28. 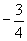 ,提示:由已知
,提示:由已知
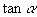 ,
,
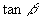 必为方程
必为方程
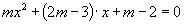 的两根,
的两根,
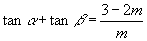 ,
,
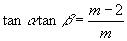 ,故
,故
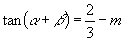 ,又由△≥0
,又由△≥0 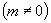 ,得
,得
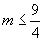
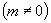 ,怕以
,怕以
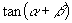 的最小值是
的最小值是
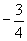 .
.
4.7 二倍角的正弦、余弦、正切
教学目标
1.掌握倍角公式的推导,从中体会数学的化归思想和数学规律发现的过程; 2.掌握二倍角的正弦、余弦、正切公式,能正确运用这些公式进行简单的三角函数式的化简、求值和恒等式的证明; 3.通过综合运用公式,使学生掌握有关技巧,提高学生分析问题,解决问题的能力; 4.通过以上公式的推导,了解半角公式间以及它们与和角公式之间的内在联系,从而培养学生的逻辑推理能力和辩证唯物主义观点.
教学建议
1.倍角公式可以由学生根据和角公式直接推导出,在对 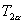 公式的推导中让学生完善角的范围限制.公式推出后,让学生将倍角和前面所学的和(差)角公式的联系图总结出来,使知识系统化.
公式的推导中让学生完善角的范围限制.公式推出后,让学生将倍角和前面所学的和(差)角公式的联系图总结出来,使知识系统化.
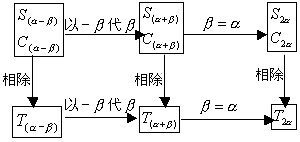
2.由学生讨论分析公式的特点.①公式中的角之间存在2倍关系,其中要强调倍角的相对性,打破学生习惯认为只有  ,
,
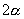 才具有2倍角关系,教学中通过一些简单实例加强这方面的训练,熟悉公式的正向、逆向运用,如
才具有2倍角关系,教学中通过一些简单实例加强这方面的训练,熟悉公式的正向、逆向运用,如 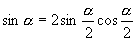 ,
,
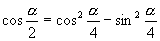 ,
,
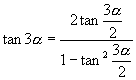 ,
,
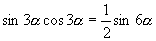 ,
,
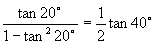 等.②利用
等.②利用 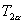 求
求
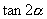 只需要已知
只需要已知
 即可,利用
即可,利用
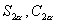 求
求
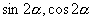 时需要已知
时需要已知
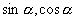 ,观察
,观察
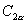 左侧的特点,可以与
左侧的特点,可以与
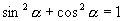 建立联系,能否将公式变形?引导学生推导出
建立联系,能否将公式变形?引导学生推导出
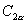 的两个变形公式,因此已知
的两个变形公式,因此已知
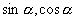 中之一即可求出
中之一即可求出
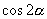 .③由单角变为倍角时式子的幂降升高,相反由倍角变为单角时式子的幂降低,在求解、化简或证明时要注意分析角之间、式子幂之间的关系,整理将形式统一.
3.讲解例1时给学生指出或让学生归纳出:已知角
.③由单角变为倍角时式子的幂降升高,相反由倍角变为单角时式子的幂降低,在求解、化简或证明时要注意分析角之间、式子幂之间的关系,整理将形式统一.
3.讲解例1时给学生指出或让学生归纳出:已知角
 的某个三角函数值及其角所在的象限不仅可以求出
的某个三角函数值及其角所在的象限不仅可以求出
 其余的三角函数值,还可求倍角的三角函数值.
4.课本在例2的分析中给出将结论变形求解的方法,学生感觉方法巧妙的同时,还困惑理解方法如何想到的,给学生分析:证明三角等式一般要观察分析等式两边的联系区别,主要从角和函数名称入手,尽量将角和函数名称统一,此题左右两侧的角形式和函数名称都相同,分子中的角都是 4倍的、函数名称都是正弦、余弦,分母上都是单角而且函数名是正切,直接从左或右向另一侧证明有些困难,能否将结论适当的变形以便于求解?使学生了解整个题目分析的过程.
5.解决本章开始所提的问题,是倍角公式的实际应用,利用三角函数线学生可以得到
其余的三角函数值,还可求倍角的三角函数值.
4.课本在例2的分析中给出将结论变形求解的方法,学生感觉方法巧妙的同时,还困惑理解方法如何想到的,给学生分析:证明三角等式一般要观察分析等式两边的联系区别,主要从角和函数名称入手,尽量将角和函数名称统一,此题左右两侧的角形式和函数名称都相同,分子中的角都是 4倍的、函数名称都是正弦、余弦,分母上都是单角而且函数名是正切,直接从左或右向另一侧证明有些困难,能否将结论适当的变形以便于求解?使学生了解整个题目分析的过程.
5.解决本章开始所提的问题,是倍角公式的实际应用,利用三角函数线学生可以得到 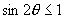 ,得到本题的结论.另外还需要把题目中“半圆”的条件替换为“圆”,可以的得到正方形的性质:在一个圆的所有内接矩形中,内接正方形的面积为最大.
6.例4、5是利用和(差)角、倍角公式推导出了半角公式、和差化积以及积化和差,这些公式不要求记忆,但要求学生在给出公式时会利用这些公式,掌握公式的推导过程.
,得到本题的结论.另外还需要把题目中“半圆”的条件替换为“圆”,可以的得到正方形的性质:在一个圆的所有内接矩形中,内接正方形的面积为最大.
6.例4、5是利用和(差)角、倍角公式推导出了半角公式、和差化积以及积化和差,这些公式不要求记忆,但要求学生在给出公式时会利用这些公式,掌握公式的推导过程.
教学设计示例(一)
二倍角的正弦、余弦、正切(第一课时)
23.已知 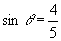 ,
,
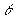 是第二象限角,又
是第二象限角,又
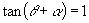 ,则
,则
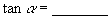 .
.
22.已知 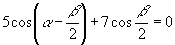 ,则
,则
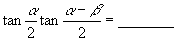 .
.
21.若 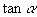 ,
,
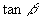 是方程
是方程
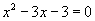 的两个根,则
的两个根,则
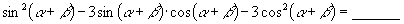 .
.
20.已知 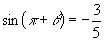 ,
,
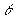 是第二象限角,
是第二象限角,
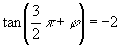 ,
,
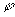 是第三象限角,则
是第三象限角,则
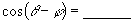 .
.
19.已知 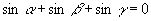 ,
,
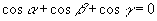 ,则
,则
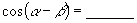 .
.
18.若 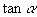 ,
,
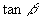 是方程
是方程
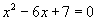 的两个根,则
的两个根,则
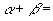 ( )
( )
A.  B.
B. 
C. 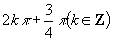 D.
D. 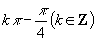
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com