
4.像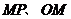 这种被看作带有方向的线段,叫做有向线段(direct line
segment).
这种被看作带有方向的线段,叫做有向线段(direct line
segment).
3.思考:(1)为了去掉上述等式中的绝对值符号,能否给线段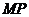 、
、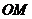 规定一个适当的方向,使它们的取值与点
规定一个适当的方向,使它们的取值与点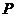 的坐标一致?
的坐标一致?
(2)你能借助单位圆,找到一条如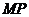 、
、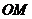 一样的线段来表示角
一样的线段来表示角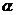 的正切值吗?
的正切值吗?
我们知道,指标坐标系内点的坐标与坐标轴的方向有关.当角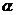 的终边不在坐标轴时,以
的终边不在坐标轴时,以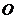 为始点、
为始点、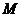 为终点,规定:
为终点,规定:
当线段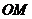 与
与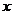 轴同向时,
轴同向时,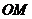 的方向为正向,且有正值
的方向为正向,且有正值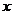 ;当线段
;当线段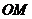 与
与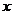 轴反向时,
轴反向时,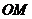 的方向为负向,且有正值
的方向为负向,且有正值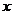 ;其中
;其中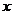 为
为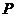 点的横坐标.这样,无论那种情况都有
点的横坐标.这样,无论那种情况都有
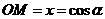
同理,当角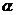 的终边不在
的终边不在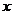 轴上时,以
轴上时,以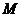 为始点、
为始点、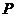 为终点,规定:
为终点,规定:
当线段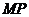 与
与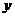 轴同向时,
轴同向时,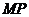 的方向为正向,且有正值
的方向为正向,且有正值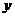 ;当线段
;当线段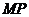 与
与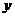 轴反向
轴反向
时,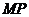 的方向为负向,且有正值
的方向为负向,且有正值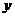 ;其中
;其中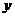 为
为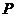 点的横坐标.这样,无论那种情况都有
点的横坐标.这样,无论那种情况都有
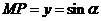
2.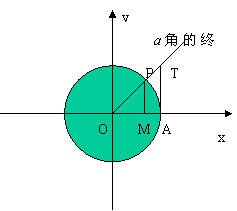 [边描述边画]以坐标原点为圆心,以单位长度1为半径画一个圆,这个圆就叫做单位圆(注意:这个单位长度不一定就是1厘米或1米).当角
[边描述边画]以坐标原点为圆心,以单位长度1为半径画一个圆,这个圆就叫做单位圆(注意:这个单位长度不一定就是1厘米或1米).当角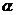 为第一象限角时,则其终边与单位圆必有一个交点
为第一象限角时,则其终边与单位圆必有一个交点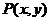 ,过点
,过点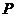 作
作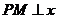 轴交
轴交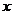 轴于点
轴于点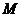 ,则请你观察:
,则请你观察:
根据三角函数的定义: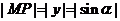 ;
;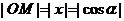
随着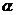 在第一象限内转动,
在第一象限内转动,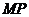 、
、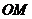 是否也跟着变化?
是否也跟着变化?
1.引入:角是一个图形概念,也是一个数量概念(弧度数).作为角的函数--三角函数是一个数量概念(比值),但它是否也是一个图形概念呢?换句话说,能否用几何方式来表示三角函数呢?
5、 三角函数的定义域.
要求:记忆.并指出,三角函数没有定义的地方一定是在轴上角,所以,凡是碰到轴上角时,要结合定义进行分析;并要求在理解的基础上记忆.
[探究新知]
4、 诱导公式(一):终边相同的角的同一三角函数的值相等;
3、 三角函数在轴上角的值;
2、 三角函数在各象限角的符号;
1、 三角函数的定义;
2.比较角概念推广以后,三角函数定义的变化.思考公式一的本质是什么?要做到熟练应用.另外,关于三角函数值在各象限的符号要熟练掌握,知道推导方法.
第二课时 任意角的三角函数(二)
[复习回顾]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com