
13.正方形ABCD与正方形ABEF所在平面相交于AB,在AE、BD上各有一点P、Q,且AP=DQ.求证:PQ∥平面BCE.
证明 方法一 如图所示,作PM∥AB交BE于M,作QN∥AB交BC于N,连接MN.
∵正方形ABCD和正方形ABEF有公共边AB,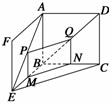 ∴AE=BD.
∴AE=BD.
又∵AP=DQ,∴PE=QB, 又∵PM∥AB∥QN,
∴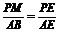 ,
,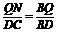 ,∴
,∴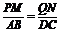 .
.
 ∴PM QN,
∴PM QN,
∴四边形PMNQ为平行四边形,∴PQ∥MN.又MN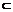 平面BCE,PQ
平面BCE,PQ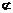 平面BCE,
平面BCE,
∴PQ∥平面BCE.
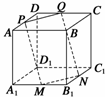
12.如图所示,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?
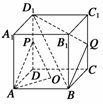 解 当Q为CC1的中点时,平面D1BQ∥平面PAO.
解 当Q为CC1的中点时,平面D1BQ∥平面PAO.
∵Q为CC1的中点,P为DD1的中点,∴QB∥PA.
∵P、O为DD1、DB的中点,∴D1B∥PO.
又PO∩PA=P,D1B∩QB=B, D1B∥平面PAO,QB∥平面PAO,
∴平面D1BQ∥平面PAO.
11.如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M,N分别是下底面的棱A1B1,B1C1的中点,
P是上底面的棱AD上的一点,AP=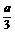 ,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ=
,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= 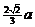 .
.
10. 考察下列三个命题,在“
”处都缺少同一个条件,补上这个条件使其构成真命题(其中l,m为不同的直线,
考察下列三个命题,在“
”处都缺少同一个条件,补上这个条件使其构成真命题(其中l,m为不同的直线,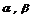
|
|
|
|
|
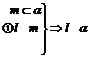
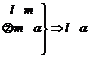
|
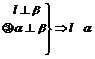
9.已知直线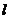 和平面
和平面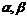 、,且
、,且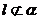 ,
,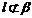 ,给出以下3个论断:
,给出以下3个论断:
①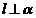 , ②
, ②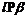 , ③
, ③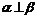 .从中任取两个作为条件,剩下的一个作为结论,则( )
.从中任取两个作为条件,剩下的一个作为结论,则( )
A.一共可以写出6个命题,其中有2个命题正确 B.一共可以写出3个命题,其中有2个命题正确
C.一共可以写出6个命题,这6个命题都正确 D.一共可以写出3个命题,这3个命题都正确
8、下列说法正确的是( )
A.直线  平行于平面α内的无数条直线,则
平行于平面α内的无数条直线,则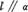 B.若直线a在平面α外,则a∥α
B.若直线a在平面α外,则a∥α
C.若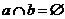 ,
, 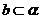 ,则
,则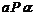 D.若
D.若 ,
,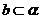 ,那么直线
,那么直线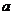 就平行于平面
就平行于平面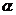 内的无数条直线
内的无数条直线
7.已知直线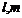 和平面
和平面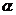 ,则
,则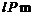 的一个充分但不必要的条件是( )
的一个充分但不必要的条件是( )
A. 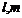 与
与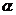 成等角 B.
成等角 B.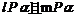 C.
C. 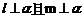 D.
D. 
6.给出下列关于互不相同的直线m,l,n和平面 ,
, 的四个命题:
的四个命题:
①若m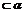 ,l∩
,l∩ =A,点A
=A,点A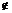 m,则l与m不共面;②若m,l是异面直线,l∥
m,则l与m不共面;②若m,l是异面直线,l∥ ,m∥
,m∥ ,且n⊥l,n⊥m,则n⊥
,且n⊥l,n⊥m,则n⊥ ;③若l∥
;③若l∥ ,m∥
,m∥ ,
, ∥
∥ ,则l∥m; ④若l
,则l∥m; ④若l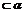 ,m
,m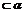 ,l∩m=A,l∥
,l∩m=A,l∥ ,m∥
,m∥ ,则
,则 ∥
∥ . 其中为假命题的是( C ) A.①? B.②? C.③ D.④
. 其中为假命题的是( C ) A.①? B.②? C.③ D.④
5.(2008·湖南理,5)设有直线m、n和平面 、
、 .下列四个命题中,正确的是 ( D )
.下列四个命题中,正确的是 ( D )
?A.若m∥ ,n∥
,n∥ ,则m∥n? B.若m
,则m∥n? B.若m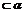 ,n
,n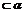 ,m∥
,m∥ ,n∥
,n∥ ,则
,则 ∥
∥
?C.若 ⊥
⊥ ,m
,m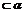 ,则m⊥
,则m⊥ ? D.若
? D.若 ⊥
⊥ ,m⊥
,m⊥ ,m
,m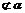 ,则m∥
,则m∥
4.(2008·海南,宁夏文,12)已知平面 ⊥平面
⊥平面 ,
, ∩
∩ =l,点A∈
=l,点A∈ ,A
,A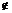 l,直线AB∥l,直线AC⊥l,直线m∥
l,直线AB∥l,直线AC⊥l,直线m∥ ,m∥
,m∥ ,则下列四种位置关系中,不一定成立的是 (
D
)
,则下列四种位置关系中,不一定成立的是 (
D
)
?A.AB∥m? B.AC⊥m? C.AB∥ ? D.AC⊥
? D.AC⊥
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com