
1、揭示历史时间的顺序性特征
所谓顺序性是指历史活动时间的先后更替承接。如中国近代史上的鸦片战争、太平天国运动、第二次鸦片战争、中法战争、中日战争、义和团运动、八国联军侵华、辛亥革命等,是按 1840─1842年、1851─1864年、1856─1860年、1883─1885年、1894─1895年、1899─1900年、1911年的时间先后顺序更替的。在这一更替过程中,外国侵略的逐步扩大加深以及与之相联系的中国人民反抗斗争的前赴后继,脉络清晰,一定程度上反映了历史的内在联系及其规律性。按照时间顺序学习历史既与人们的生活经验及学习心理相贴近,也符合秩序渐进性教学原则。
15.(南开中学高2010级高三12月月考试卷)
已知二次函数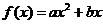 (
(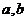 为常数且
为常数且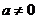 )满足
)满足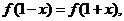 且方程
且方程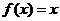 有等根.
有等根.
(1)求 的解析式;
的解析式;
(2)设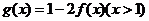 的反函数为
的反函数为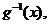 若
若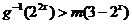 对
对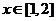 恒成立,求实数
恒成立,求实数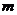 的取值范围.
的取值范围.
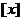 表示不超过
表示不超过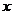 的最大整数,正项数列
的最大整数,正项数列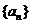 满足
满足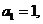
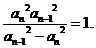
(1)求数列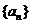 的通项公式
的通项公式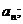
(2)求证: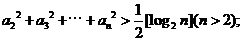
(3)已知数列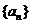 的前
的前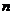 项和为
项和为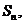 求证:当
求证:当 时,有
时,有
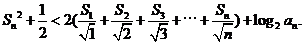


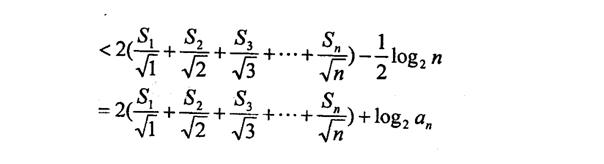
14.(万州二中高三12月考试数学试题(理)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点。如果函数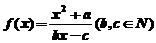 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且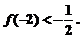
⑴求函数f(x)的解析式;
⑵已知各项不为零的数列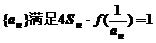 (
(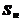 为
为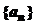 数列前n项和),求数列通项
数列前n项和),求数列通项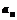 ;
;
⑶如果数列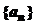 满足
满足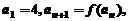 ,求证:当
,求证:当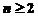 时,恒有
时,恒有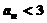 成立.
成立.
⑴ 依题意有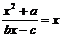 ,化简为
,化简为 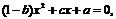 由fnh 达定理, 得
由fnh 达定理, 得
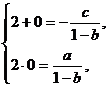
解得 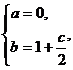 ……………2分
……………2分
代入表达式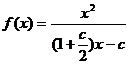 ,由
,由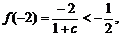
得 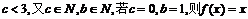 ,不满足题意
,不满足题意
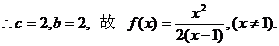 ………………4分
………………4分
⑵由题设得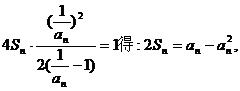 (*)
(*)
且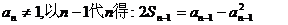 (**)
(**)
………………6分
由(*)与(**)两式相减得:
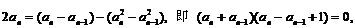
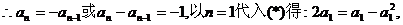
解得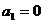 (舍去)或
(舍去)或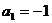 ,由
,由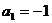 ,若
,若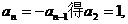 这与
这与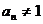 矛盾,
矛盾,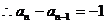 ,即{
,即{ 是以-1为首项,-1为公差的等差数列,
是以-1为首项,-1为公差的等差数列,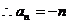 . ……8分
. ……8分
⑶采用反证法,假设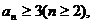 则由(I)知
则由(I)知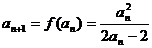
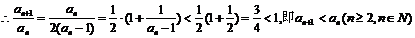 ,
,
有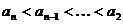 ,而当
,而当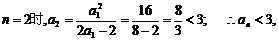
这与假设矛盾,故假设不成立. ∴an<3 ……………12分
13.(吉林一中高三第四次“教与学”质量检测)
设函数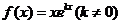
(1)求曲线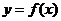 在点
在点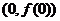 处的切线方程;
处的切线方程;
(2)求函数 的单调区间;
的单调区间;
(3)若函数 在区间
在区间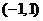 内单调递增,求
内单调递增,求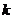 的取值范围.
的取值范围.
(Ⅰ)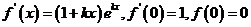 ,
,
曲线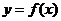 在点
在点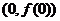 处的切线方程为
处的切线方程为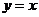 .…………3分
.…………3分
(Ⅱ)由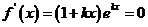 ,得
,得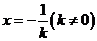 ,
,
若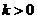 ,则当
,则当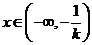 时,
时,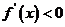 ,函数
,函数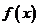 单调递减,
单调递减,
当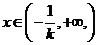 时,
时,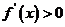 ,函数
,函数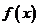 单调递增,………6分
单调递增,………6分
若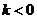 ,则当
,则当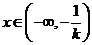 时,
时,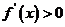 ,函数
,函数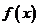 单调递增,
单调递增,
当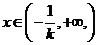 时,
时,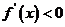 ,函数
,函数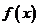 单调递减,…………9分
单调递减,…………9分
(Ⅲ)由(Ⅱ)知,若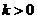 ,则当且仅当
,则当且仅当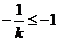 ,
,
即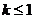 时,函数
时,函数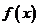
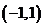 内单调递增,
内单调递增,
若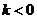 ,则当且仅当
,则当且仅当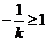 ,
,
即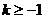 时,函数
时,函数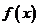
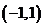 内单调递增,
内单调递增,
综上可知,函数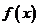
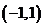 内单调递增时,
内单调递增时,
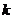 的取值范围是
的取值范围是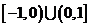 .…………12分 (也可用恒成立解决)
.…………12分 (也可用恒成立解决)
12.(广东省六所名校2010届高三第三次联考)
 如果对于函数
如果对于函数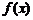 的定义域内任意的
的定义域内任意的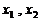 ,都有
,都有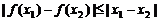 成立,那么就称函数
成立,那么就称函数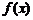 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.
(1)判断函数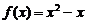 ,
,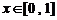 是否是“平缓函数”;
是否是“平缓函数”;
(2)若函数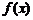 是闭区间
是闭区间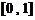 上的“平缓函数”,且
上的“平缓函数”,且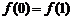 .证明:对于任意
.证明:对于任意
的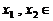
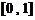 ,都有
,都有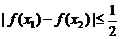 成立.
成立.
(3)设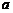 、
、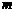 为实常数,
为实常数,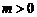 .若
.若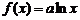 是区间
是区间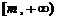 上的“平缓函数”,试估计
上的“平缓函数”,试估计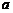 的取值范围(用
的取值范围(用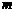 表示,不必证明).
表示,不必证明).
已知数列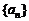 的前
的前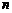 项和
项和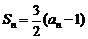 ,
,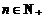 .
.
(1)求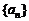 的通项公式;
的通项公式;
(2)设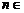 N+,集合
N+,集合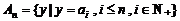 ,
,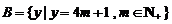 .现在集合
.现在集合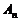 中随机取一个元素
中随机取一个元素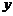 ,记
,记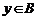 的概率为
的概率为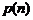 ,求
,求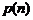 的表达式.
的表达式.
解:(1)因为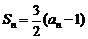 ,
,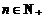 ,所以
,所以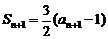 .
.
两式相减,得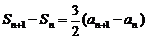 ,即
,即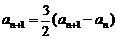 ,
,
∴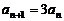 ,
,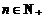 .…………………………3分
.…………………………3分
又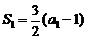 ,即
,即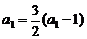 ,所以
,所以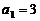 .
.
∴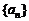 是首项为3,公比为3的等比数列.
是首项为3,公比为3的等比数列.
从而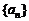 的通项公式是
的通项公式是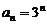 ,
,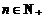 .………………………6分
.………………………6分
(2)设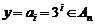 ,
,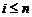 ,
,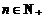 .
.
 当
当 ,
,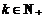 时,
时,
∵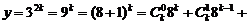 …
…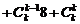
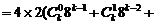 …
…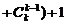 ,∴
,∴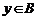 . ………………………9分
. ………………………9分
当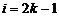 ,
,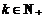 时,
时,
∵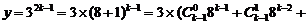 …
…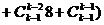
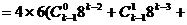 …
…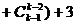 ,∴
,∴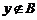 .…………………12分
.…………………12分
又∵集合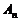 含
含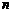 个元素,
个元素,
∴在集合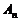 中随机取一个元素
中随机取一个元素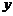 ,有
,有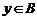 的概率
的概率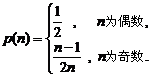 .……………………14分
.……………………14分
证明:(1)对于任意的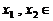
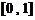 ,
,
有 ,
,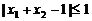 .…………………………2分
.…………………………2分
从而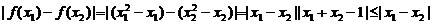 .
.
∴函数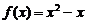 ,
,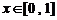 是“平缓函数”. ………………………4分
是“平缓函数”. ………………………4分
(2)当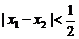 时,由已知得
时,由已知得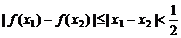 ; ……………6分
; ……………6分
当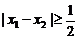 时,因为
时,因为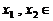
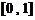 ,不妨设
,不妨设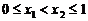 ,其中
,其中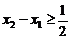 ,
,
因为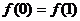 ,所以
,所以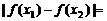
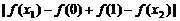
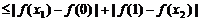
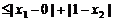
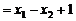
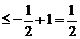 .
.
故对于任意的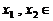
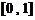 ,都有
,都有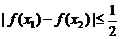 成立. ………………………10分
成立. ………………………10分
 (3)结合函数
(3)结合函数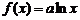 的图象性质及其在点
的图象性质及其在点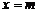 处的切线斜率,估计
处的切线斜率,估计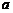 的取值范围是闭区间
的取值范围是闭区间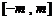 .…………………………(注:只需直接给出正确结
.…………………………(注:只需直接给出正确结
11.(上海市格致中学2010届高三上学期期中考试)
已知函数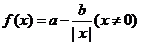 。
。
(1)若函数 是
是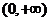 上的增函数,求实数
上的增函数,求实数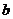 的取值范围;
的取值范围;
(2)当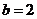 时,若不等式
时,若不等式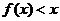 在区间
在区间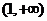 上恒成立,求实数
上恒成立,求实数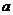 的取值范围;
的取值范围;
(3)对于函数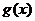 若存在区间
若存在区间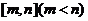 ,使
,使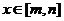 时,函数
时,函数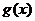 的值域也是
的值域也是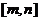 ,则称
,则称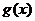 是
是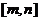 上的闭函数。若函数
上的闭函数。若函数 是某区间上的闭函数,试探求
是某区间上的闭函数,试探求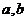 应满足的条件。
应满足的条件。
解:(1) 当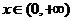 时,
时,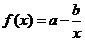
设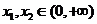 且
且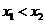 ,由
,由 是
是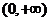 上的增函数,则
上的增函数,则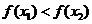 2分
2分
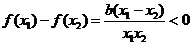 3分
3分
由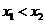 ,
,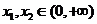 知
知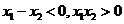 ,所以
,所以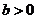 ,即
,即 5分
5分
(2)当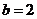 时,
时,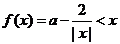 在
在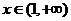 上恒成立,即
上恒成立,即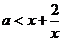 6分
6分
因为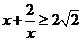 ,当
,当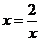 即
即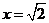 时取等号, 8分
时取等号, 8分
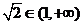 ,所以
,所以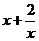 在
在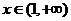 上的最小值为
上的最小值为 。则
。则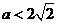 10分
10分
(3)因为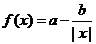 的定义域是
的定义域是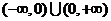 ,设
,设 是区间
是区间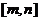 上的闭函数,则
上的闭函数,则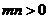 且
且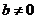 11分
11分
①若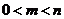
当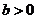 时,
时,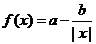 是
是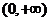 上的增函数,则
上的增函数,则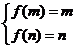 ,
,
所以方程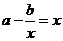 在
在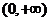 上有两不等实根,
上有两不等实根,
即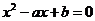 在
在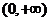 上有两不等实根,所以
上有两不等实根,所以
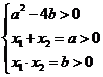 ,即
,即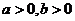 且
且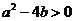 13分
13分
当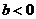 时,
时,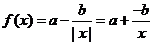 在
在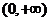 上递减,则
上递减,则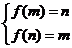 ,即
,即
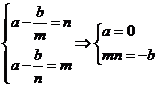 ,所以
,所以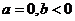 14分
14分
②若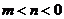
当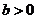 时,
时,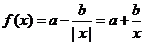 是
是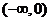 上的减函数,所以
上的减函数,所以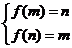 ,即
,即
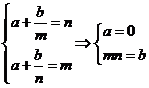 ,所以
,所以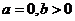 15分
15分
当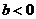
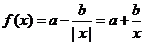 是
是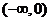 上的增函数,所以
上的增函数,所以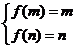 所以方程
所以方程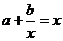 在
在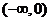 上有两不等实根,即
上有两不等实根,即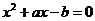 在
在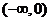 上有两不等实根,
上有两不等实根,
所以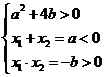 即
即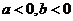 且
且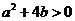 17分
17分
综上知: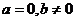 或
或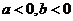 且
且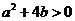 或
或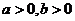 且
且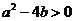 。
。
即: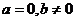 或
或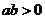 且
且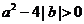
10.(上海师大附中2010届高三上学期期中考试)
已知函数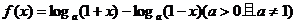
(1)讨论 的奇偶性与单调性;
的奇偶性与单调性;
(2)若不等式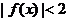 的解集为
的解集为 的值;
的值;
(3)(文)设 的反函数为
的反函数为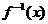 ,若关于
,若关于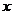 的不等式
的不等式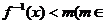 R)有解,求
R)有解,求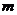 的取值范围.
的取值范围.
(理)设 的反函数为
的反函数为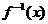 ,若
,若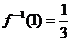 ,解关于
,解关于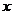 的不等式
的不等式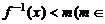 R).
R).
(1)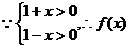 定义域为
定义域为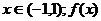 为奇函数;
为奇函数;
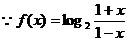 ,
,
①当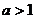 时,在定义域内为增函数;
时,在定义域内为增函数;
②当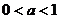 时,在定义域内为减函数;
时,在定义域内为减函数;
(2)①当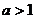 时,∵
时,∵ 在定义域内为增函数且为奇函数,
在定义域内为增函数且为奇函数,
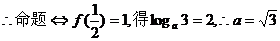 ;
;
②当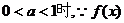 在定义域内为减函数且为奇函数,
在定义域内为减函数且为奇函数,
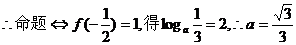 ;
;
(3)(文)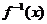 的值域为
的值域为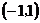 ,关于
,关于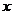 的不等式
的不等式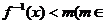 R)有解的充要条件是
R)有解的充要条件是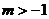
(理)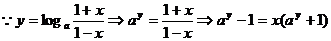
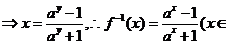 R);
R);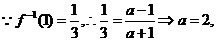
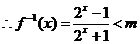 ,
,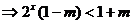 ;
;
①当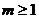 时,不等式解集为
时,不等式解集为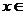 R;
R;
②当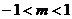 时,得
时,得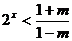 ,不等式的解集为
,不等式的解集为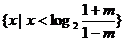 ;
;
③当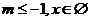
1.
已知曲线C: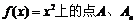 的横坐标分别为1和
的横坐标分别为1和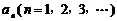 ,且a1=5,数列{xn}满足xn+1 = tf (xn –
1) + 1(t > 0且
,且a1=5,数列{xn}满足xn+1 = tf (xn –
1) + 1(t > 0且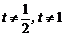 ).设区间
).设区间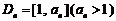 ,当
,当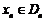 时,曲线C上存在点
时,曲线C上存在点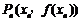 使得xn的值与直线AAn的斜率之半相等.
使得xn的值与直线AAn的斜率之半相等.
(1)
证明: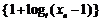 是等比数列;
是等比数列;
(2)
当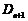
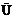
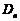 对一切
对一切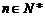 恒成立时,求t的取值范围;
恒成立时,求t的取值范围;
(3) 记数列{an}的前n项和为Sn,当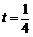 时,试比较Sn与n + 7的大小,并证明你的结论.
时,试比较Sn与n + 7的大小,并证明你的结论.
解:(1) ∵由已知得 ∴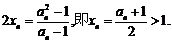
由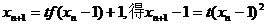
∴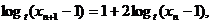 即
即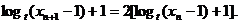
∴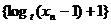 是首项为
是首项为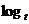 2+1为首项,公比为2的等比数列. ······ 4分
2+1为首项,公比为2的等比数列. ······ 4分
(2) 由(1)得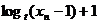 =(
=(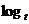 2+1)·2n-1,∴
2+1)·2n-1,∴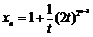
从而an=2xn-1=1+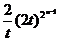 ,由Dn+1
,由Dn+1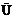 Dn,得an+1<an,即
Dn,得an+1<an,即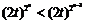 .
.
∴0<2t<1,即0<t< ··············································································· 9分
··············································································· 9分
(3) 当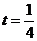 时,
时,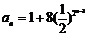
∴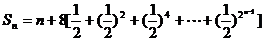
不难证明:当n≤3时,2n-1≤n+1;当n≥4时,2n-1>n+1.
∴当n≤3时,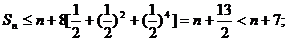
当n≥4时,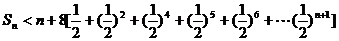
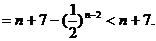
综上所述,对任意的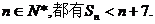 ·········································· 13分
·········································· 13分
9.(西南师大附中高2010级第四次月考)
2.解(1)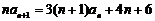 ,两边同除以
,两边同除以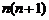 得:
得:
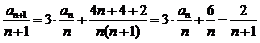
∴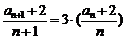
∴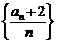 是首项为
是首项为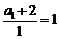 ,公比
,公比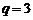 的等比数列………………4分
的等比数列………………4分
∴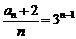
∴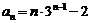
(2)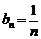 ,当
,当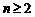 时,
时,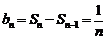 ,
,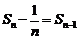 ………………5分
………………5分
两边平方得: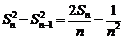

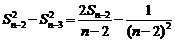
……
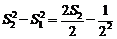
相加得: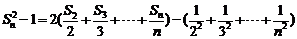
又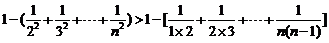
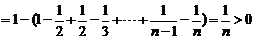
∴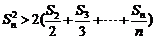 …………………………………………9分
…………………………………………9分
(3)(数学归纳法)
当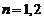 时,显然成立
时,显然成立
当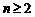 时,证明加强的不等式
时,证明加强的不等式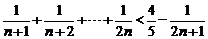
假设当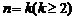 时命题成立,即
时命题成立,即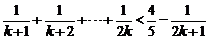
则当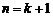 时
时
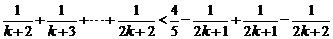
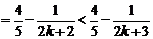
∴当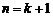 时命题成立,故原不等式成立……………………14分
时命题成立,故原不等式成立……………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com