
17.(I)证明: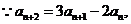
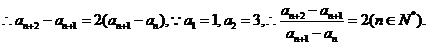
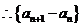 是以
是以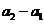
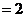 为首项,2为公比的等比数列。
为首项,2为公比的等比数列。
(II)解:由(I)得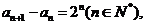
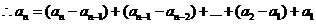
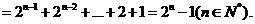
(III)证明: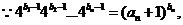
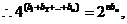
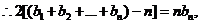 ①
①
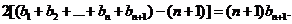 ②
②
②-①,得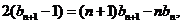 即
即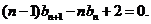 ③
③
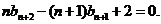 ④
④
④-③,得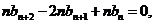 即
即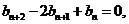
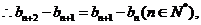
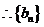 是等差数列。
是等差数列。
15.-2 提示:由题意可知q≠1,∴可得2(1-qn)=(1-qn+1)+(1-qn+2),即q2+q-2=0,解得q=-2或q=1(不合题意,舍去),∴q=-2.
16 解:13 解
解 ∵10Sn=an2+5an+6,
① ∴10a1=a12+5a1+6,解之得a1=2或a1=3.
∵10Sn=an2+5an+6,
① ∴10a1=a12+5a1+6,解之得a1=2或a1=3.
又10Sn-1=an-12+5an-1+6(n≥2),②
由①-②得 10an=(an2-an-12)+6(an-an-1),即(an+an-1)(an-an-1-5)=0
∵an+an-1>0 , ∴an-an-1=5 (n≥2).
当a1=3时,a3=13,a15=73. a1, a3,a15不成等比数列∴a1≠3;
当a1=2时, a3=12, a15=72, 有 a32=a1a15 , ∴a1=2, ∴an=5n-3.
12. 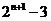 解:在数列
解:在数列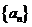 中,若
中,若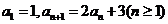 ,∴
,∴ 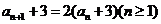 ,即{
,即{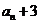 }是以
}是以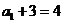 为首项,2为公比的等比数列,
为首项,2为公比的等比数列,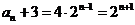 ,所以该数列的通项
,所以该数列的通项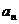
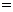
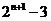 .
.
13 (-∞,8) 提示
(-∞,8) 提示 解出a、b,解对数不等式即可
解出a、b,解对数不等式即可 答案
答案 (-∞,8)
(-∞,8)
14 a11=29 提示
a11=29 提示 利用S奇/S偶=
利用S奇/S偶=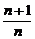 得解
得解 答案
答案 第11项a11=29
第11项a11=29
11.(文)解:设等差数列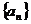 的首项为a1,公差为d,由题意得
的首项为a1,公差为d,由题意得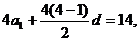
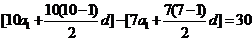 ,联立解得a1=2,d=1,所以S9=
,联立解得a1=2,d=1,所以S9=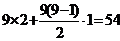
7.A 提示:由a1=0,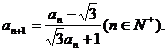 得a2=-
得a2=-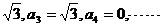
由此可知:数列{an}是周期变化的,且三个一循环,所以可得:a20=a2=-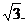 故选A
故选A
8 A
解:由等差数列的求和公式可得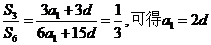 且
且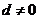
所以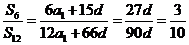 ,故选A
,故选A
点评:本题主要考察等比数列的求和公式,难度一般
9 C 解:在等差数列{an}中,a2+a8=8,∴ 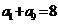 ,则该数列前9项和S9=
,则该数列前9项和S9=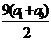 =36,选C
=36,选C
10 C 解:数列 、
、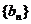 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为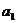 、
、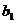 ,且
,且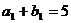 ,
,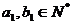 .设
.设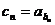 (
( ),则数列
),则数列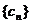 的前10项和等于
的前10项和等于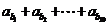 =
=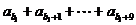 ,
,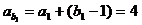 ,∴
,∴ 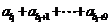
=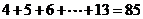 ,选C.
,选C.
18.(山东卷)已知数列{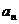 }中,
}中,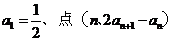 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(Ⅰ)令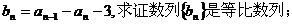 (Ⅱ)求数列
(Ⅱ)求数列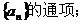
(Ⅲ)设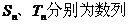
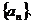
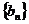 的前n项和,是否存在实数
的前n项和,是否存在实数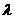 ,使得数列
,使得数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出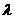 .若不存在,则说明理由。
.若不存在,则说明理由。
答案与点拨:
1 B 解:由等比数列的性质可得ac=(-1)×(-9)=9,b×b=9且b与奇数项的符号相同,故b=-3,选B
2 B解:在等差数列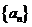 中,已知
中,已知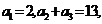 ∴ d=3,a5=14,
∴ d=3,a5=14,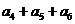 =3a5=42,选B.
=3a5=42,选B.
3 D解: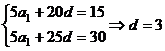 ,故选C.
,故选C.
4 D解:由互不相等的实数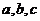 成等差数列可设a=b-d,c=b+d,由
成等差数列可设a=b-d,c=b+d,由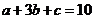 可得b=2,所以a=2-d,c=2+d,又
可得b=2,所以a=2-d,c=2+d,又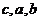 成等比数列可得d=6,所以a=-4,选D
成等比数列可得d=6,所以a=-4,选D
5 A解:依题意,a1+a200=1,故选A
6 (文)C 解:因数列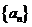 为等比,则
为等比,则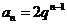 ,因数列
,因数列 也是等比数列,
也是等比数列,
则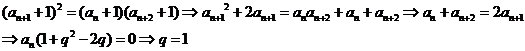
即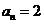 ,所以
,所以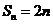 ,故选择答案C。
,故选择答案C。
16 已知正项数列
已知正项数列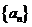 ,其前
,其前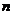 项和
项和 满足
满足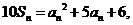 且
且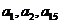 成等比数列,求数列
成等比数列,求数列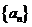 的通项
的通项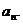
17.(文科做)(06福建)已知数列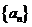 满足
满足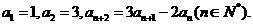
(I)证明:数列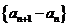 是等比数列; (II)求数列
是等比数列; (II)求数列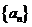 的通项公式;
的通项公式;
(II)若数列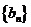 满足
满足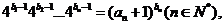 证明
证明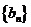 是等差数
是等差数
15.设等比数列 的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为 .
的公比为q,前n项和为Sn,若Sn+1,Sn,Sn+2成等差数列,则q的值为 .
14. 等差数列{an}共有2n+1项,其中奇数项之和为319,偶数项之和为290,则其中间项为_________
13. 已知a,b,a+b成等差数列,a,b,ab成等比数列,且0<logm(ab)<1,则m的取值范围是________ _
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com