4．如图所示，a、b、c为电场中同一条水平方向电场线上的三点，c为ab中点．a、b电势分别为，．下列叙述正确的是

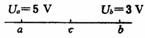A．该电场在c点处的电势一定为4 V

B．a点处的场强一定大于b点处的场强

C．一正电荷从c点运动到b点电势能一定减少

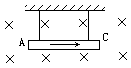D．一正电荷运动到c点时受到的电场力由c指向a

3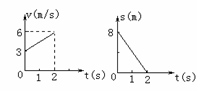．质量为2kg的物体在x-y平面上做曲线运动，在x方向的速度图像和y方向的位移图像如图所示，下列说法正确的是

A．质点的初速度为5m/s

B．质点所受的合外力为3N

C．质点初速度的方向与合外力方向垂直

D．2s末质点速度大小为6m/s

2．一个物体受到恒定的合力作用而做曲线运动，则下列说法正确的是　

A．物体的速率可能不变

B．物体一定做匀变速曲线运动，且速率一定增大

C．物体可能做匀速圆周运动

D．物体受到的合力与速度的夹角一定越来越小，但总不可能为0

1．假设地球同步卫星的轨道半径是地球半径的n倍，则

A．同步卫星运行速度是第一宇宙速度的倍

B．同步卫星的运行速度是第一宇宙速的倍

C．同步卫星的运行速度是地球赤道上物体随地球自转速度的n倍

D．同步卫星的向心加速度是地球表面重力加速度的倍

(17)(本小题满分14分)

已知中，，，，记，　 (Ⅰ)求关于的表达式；

(Ⅱ)求的值域.

(18)(本小题满分14分)

某食品企业一个月内被消费者投诉的次数用表示，据统计，随机变量的概率分布如下：

	0	1	2	3
p	0.1	0.3	2a	a

(Ⅰ)求a的值和的数学期望；

(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.　　

(19)(本小题满分14分)

在直三棱柱中，，，且异面直线与 所成的角等于，设．

　　 (Ⅰ)求的值；

　　 (Ⅱ)求平面与平面所成的锐二面角的大小．

(20)(本小题满分14分)

已知A、B、C是椭圆上的三点，其中点A的坐标为，BC过椭圆m的中心，且.

(Ⅰ)求椭圆的方程；

(Ⅱ)过点的直线l(斜率存在时)与椭圆m交于两点P，Q，设D为椭圆m与y轴负半轴的交点，且.求实数t的取值范围.　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

(21)(本小题满分14分)

已知函数的图象经过点及，为数列

的前项和.

(Ⅰ)求及；

(Ⅱ)若数列满足求数列的前项和.

辽宁省锦州市2010届高三上学期期末考试

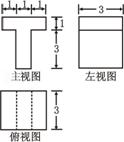(13)若某几何体的三视图(单位：)如图所示，

则此几何体的体积是　　　　　 ．　

(14)用二分法求方程x³－2x－5=0在区间[2，3]上的近似解，取区间中点x₀=2.5,那么下一个有解区间为　　　　 　　　.

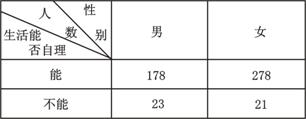
(15)从某地区15000位老人中随机抽取500人，其生活能否自理的情况如下表所示：

则该地区生活不能自理的老人中男性比女性约多＿＿＿＿＿＿人.

(16)△ABC中，A为动点，B、C为定点，B(－,0),C(,0)(其中m＞0，且m为常数)，且满足条件sinC－sinB=sinA,则动点A的轨迹方程为_________.

(1)已知集合A={x|－2≤x≤7},B={x|m+1<x<2m－1}且B≠,若A∪B=A，则

(A)－3≤m≤4　　　　　　　　　　　　　　　 (B)－3<m<4

(C)2<m<4　　　　　　　　　　　　　　　　　 (D)2<m≤4

(2)如果复数为纯虚数，则实数的值为

(A)0　　　　(B)1　　　(C)－1　　(D)0或1

(3)公差不为零的等差数列中，，数列是等比数列，且

(A)2　 　　(B)4　　 (C)8　　　 (D)16

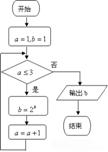(4)如右程序框图，输出的结果为

　　 (A)1　　 　 　　　　　(B)2　　　　

(C)4　　 　　　　　　　 (D)16

(5)已知函数是定义在区间上的奇函数，若，则

的最大值与最小值之和为

　　 (A)0　　　　　　 (B)2　　　　　　 (C)4　　　　　　 (D)不能确定

(6)函数的最小正周期T=

(A)2π　　　　　 (B)π　　　　　 (C)　　　　　　 (D)

(7)在空间中，有如下命题：

　　 ①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线；

②若平面∥平面，则平面内任意一条直线m∥平面；

③若平面与平面的交线为m，平面内的直线n⊥直线m，则直线n⊥平面．

其中不正确命题的个数为　　　　　　　　　　　　　　　　　　　　　　　

(A) 3　　　　　　 (B) 2　　　　　 (C) 1　　　　　　 (D) 0

(8)已知直线ax+by+c＝0与圆O：x²+y²＝1相交于A、B两点，且|AB|＝，则＝

(A)　　 　　　 　(B)　　 　 　　　(C)　　 　　　　(D)

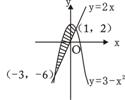(9)如右图，阴影部分的面积是　　　　　　　　　　　　　　　　　　　　　　　

　　　 (A)　　　　　　　　 (B)

　　　 (C)　　　　　　　　　 (D)

(10)锅中煮有芝麻馅汤圆6个，花生馅汤圆5个，豆沙馅汤圆4个，这三种汤圆的外部特征完全相同。从中任意舀取4个汤圆，则每种汤圆都至少取到1个的概率为　　　

(A)　　　 　　　 (B)　　 　　(C)　 　　　　(D)　　　

(11)类比“两角和与差的正余弦公式”的形式，对于给定的两个函数，，，其中，且，下面正确的运算公式是

①；

②；

③；

④．

(A)①③　　　 　　 (B)②④　 　　 (C)①④　 　　 　　(D)①②③④

(12)f(x)=，则＝

　　 (A)-23　　　　　 (B)11　　　　　 (C)19　　　　　 (D)24

第Ⅱ卷(非选择题，共90分)

(17)(本小题满分14分)

已知中，，，，记，　　　 (Ⅰ)求关于的表达式；

(Ⅱ)求的值域；

(18)(本小题满分14分)

若满足条件，求的最大值和最小值，并求出相应的值.

(19)(本小题满分14分)

在正方体中，、分别为棱、的中点．

(Ⅰ)求证：∥平面；

(Ⅱ)求证：平面⊥平面.

(20)(本小题满分14分)

已知A、B、C是椭圆上的三点，其中点A的坐标为，BC过椭圆m的中心，且.

(Ⅰ)求椭圆的方程；

(Ⅱ)过点的直线l(斜率存在时)与椭圆m交于两点P，Q，设D为椭圆m与y轴负半轴的交点，且.求实数t的取值范围.　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　

(21)(本小题满分14分)

已知函数的图象经过点及，为数列 的前项和.

(Ⅰ)求及；

(Ⅱ)若数列满足求数列的前项和.

辽宁省锦州市2010届高三上学期期末考试

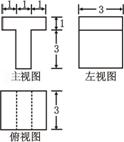(13)若某几何体的三视图(单位：)

如图所示，则此几何体的体积是　　　　　 ．　

(14)用二分法求方程x³－2x－5=0在区间[2，3]上的近似解，取区间中点x₀=2.5,那么下一个有解区间为　　　　　　 .

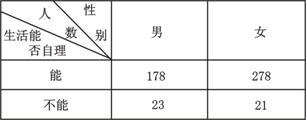
(15)从某地区15000位老人中随机抽取500人，其生活能否自理的情况如下表所示：

则该地区生活不能自理的老人中男性比女性约多__　 _____人.

(16)△ABC中，A为动点，B、C为定点，B(－,0),C(,0)(其中m＞0，且m为常数)，且满足条件sinC－sinB=sinA,则动点A的轨迹方程为_________.

(1)已知集合A={x|－2≤x≤7},B={x|m+1<x<2m－1}且B≠,若A∪B=A，则

(A)－3≤m≤4　　　　　　　　　　　　　　　 (B)－3<m<4

(C)2<m<4　　　　　　　　　　　　　　　　　 (D)2<m≤4

(2)如果复数为纯虚数，则实数的值为

(A)0　　　　(B)1　　　(C)－1　　(D)0或1

(3)公差不为零的等差数列中，，数列是等比数列，且

(A)2　　　 (B)4　　 (C)8　　　 (D)16

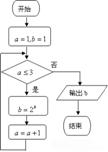
(4)如右程序框图，输出的结果为

　　 (A)1　　 　 　　　　　(B)2　　　　

(C)4　　 　　　　　　 　(D)16

(5)已知函数是定义在区间上的奇函数，若，则

的最大值与最小值之和为

　　 (A)0　　　　　　 (B)2　　　　　　 (C)4　　　　　　 (D)不能确定

(6)函数的最小正周期T=

(A)2π　　　　　 (B)π　　　　　 (C)　　　　　　 (D)

(7)在空间中，有如下命题：

　　 ①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线；

②若平面∥平面，则平面内任意一条直线m∥平面；

③若平面与平面的交线为m，平面内的直线n⊥直线m，则直线n⊥平面．

其中不正确命题的个数为　　　　　　　　　　　　　　　　　　　　　　　

(A) 3　　　　　　 (B) 2　 　　　　(C) 1　　　　　　 (D) 0

(8)已知直线ax+by+c＝0与圆O：x²+y²＝1相交于A、B两点，且|AB|＝，则＝

(A)　　 　　　 (B)　　 　 　　　(C)　　 　　　　(D)

(9)设函数的导函数，则数列的前n项和是

　　 　 　　　　　　　　 (A)　　　 (B)　　　　 (C)　 (D)

(10)某学校路口,红灯时间为30秒,黄灯时间为5秒, 绿灯时间为45秒,当你到这个路口时,看到黄灯的概率是

(A);　　　　　 (B)　 ;　　　 (C);　　　　　 (D) 　

(11)类比“两角和与差的正余弦公式”的形式，对于给定的两个函数，，，其中，且，下面正确的运算公式是

①；

②；

③；

④．

(A)①③　　　 　　 (B)②④　 　　 (C)①④　 　　　 　(D)①②③④

(12)f(x)=，则＝

　　 (A)-23　　　　　 (B)11　　　　　 (C)19　　　　 　(D)24

第Ⅱ卷(非选择题，共90分)