
4.中国人民银行定于2008年10月8日发行中国首次太空行走成功金银纪念币一套,该套纪念币共两枚,其中金币一枚,银币一枚,均为中华人民共和国法定货币。关于该纪念币,下列说法不正确的是 ( )
①具有货币的职能 ②不具有货币的职能
③是国家发行的 ④不可以流通但可以贮藏
A.①③ B.②④ C.②③ D.①④
2008年3月8日国家发改委宣布,2008年国家继续实行稻谷、小麦最低收购价政策,小麦最低收购价格调整为每50千克白小麦75元、红小麦70元、混合麦70元。根据材料回答1-3题
1.这里的稻谷.小麦 ( )
A.是商品,因为它们能满足人们的需求
B.是商品,因为它们是用于交换的劳动产品
C.不是商品,是国家收购的劳动产品
D.不是商品,是农民应该上缴给国家的劳动产品
2.这里货币执行的职能与下列选项中货币执行的职能相一致的是 ( )
A.用50元购买一本字典 B.交房租500元
C.存款利息收入200元 D.一件上衣标价300元
3.材料中国家发改委的行为体现了国家使用的调控手段是 ( )
A.经济手段 B.法律手段 C.行政手段 D.管理手段
2.求角的三个步骤:一猜,二证,三算.猜是关键,在作线面角时,利用空间图形的平行,垂直,对称关系,猜斜线上一点或斜线本身的射影一定落在平面的某个地方,然后再证
热点题型1
 例1、
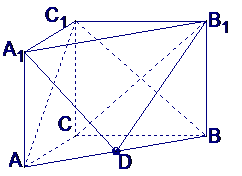
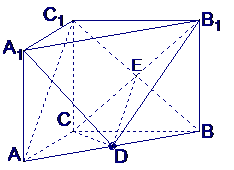
例1、 如图, 在直三棱柱
如图, 在直三棱柱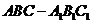 中,
中,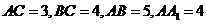 ,点
,点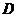 为
为
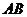 的中点.
的中点.
(Ⅰ)求证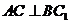 ;
;
(Ⅱ) 求证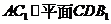 ;
;
(Ⅲ)求异面直线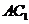 与
与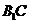 所成角的余弦值.
所成角的余弦值.
解析;异面直线所成角的平面角顶点O的选取一般
选在两异面直线的端点处,初学者或观察能力有限者可采用穷举法,实行逐 个端点考察,也有取在某线段的中点处.
个端点考察,也有取在某线段的中点处.
解:(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,
∵ DE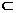 平面CDB1,AC1
平面CDB1,AC1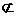 平面CDB1,∴ AC1//平面CDB1;
平面CDB1,∴ AC1//平面CDB1;
(III)∵ DE//AC1,∴ ∠CED为AC1与B1C所成的角,
 在△CED中,ED=
在△CED中,ED=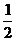 AC
AC  1=
1=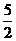 ,CD=
,CD=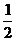 AB=
AB=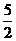 ,CE=
,CE=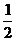 CB1=
CB1= 2
2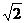 ,
,
∴ 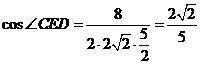 ,
,
∴ 异面直线 AC1与 B1C所成角的余弦值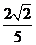 .
.
解法二: ∵直三棱锥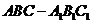 底面三边长
底面三边长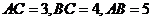 ,
,
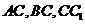 两两垂直.
两两垂直.
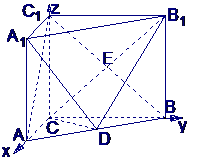
如图建立坐标系,则C(0,0,0),A(3,0,0),C1(0, 0,4),B(0,4,0),B1(0,4,4),D(
0,4),B(0,4,0),B1(0,4,4),D(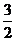 ,2,0)
,2,0)
(Ⅰ)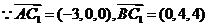 ,
,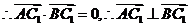 .
.
(Ⅱ)设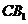 与
与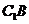 的交点为E,则E(0,2,2)
的交点为E,则E(0,2,2)
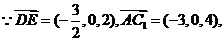
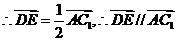
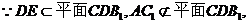
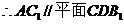 .
.
(Ⅲ)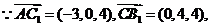
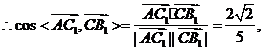
∴异面直线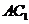 与
与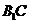 所成角的余弦值为
所成角的余弦值为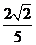 .
.
热点题型2
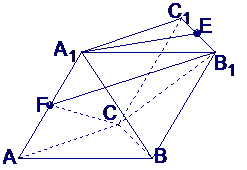 例2、如图,在斜三棱柱
例2、如图,在斜三棱柱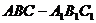 中,
中,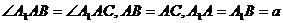 ,侧面
,侧面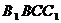 与底面ABC所成的二面角为
与底面ABC所成的二面角为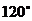 ,
, E、F分别是棱
E、F分别是棱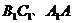 的中点
的中点
(Ⅰ)求 与底面ABC所成的角
与底面ABC所成的角
(Ⅱ)证明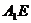 ∥平面
∥平面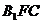
(Ⅲ)求经过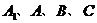 四点的球的体积.
四点的球的体积.
解:(Ⅰ)过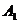 作
作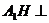 平面
平面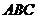 ,垂足为
,垂足为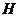 .
.
连结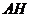 ,并延长交
,并延长交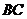 于
于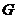 ,
,
于是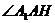
 为
为 与底面
与底面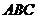 所成的角.
所成的角.
∵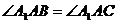 ,∴
,∴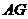 为
为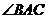 的平分线.
的平分线.
又∵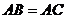 ,∴
,∴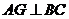 ,且
,且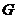 为
为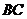 的中点.
的中点.
因此,由三垂线定理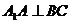 .
.
∵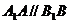 ,且
,且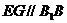 ,∴
,∴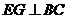 .
.
于是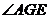 为二面角
为二面角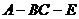 的平面角,即
的平面角,即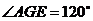 .
.
由于四边形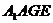 为平行四边形,得
为平行四边形,得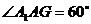 .
.
(Ⅱ)证明:设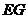 与
与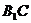 的交点为
的交点为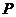 ,则点
,则点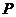 为
为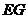 的中点.连结
的中点.连结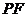 .
.
在平行四边形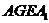 中,因
中,因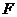 为
为 的中点,故
的中点,故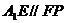 .
.
而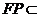
 平面
平面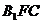 ,
,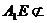 平面
平面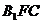 ,所以
,所以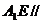 平面
平面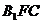 .
.
(Ⅲ)连结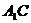 .在
.在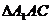 和
和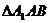 中,由于
中,由于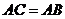 ,
,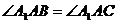 ,
,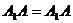 ,则
,则
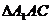 ≌
≌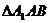 ,故
,故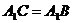 .由已知得
.由已知得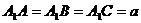 .
.
又∵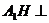 平面
平面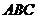 ,∴
,∴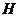 为
为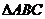 的外心.
的外心.
设所求球的球心为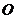 ,则
,则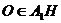 ,且球心
,且球心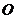 与
与 中点的连线
中点的连线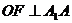 .
.
在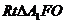 中,
中,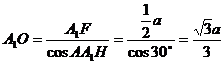 .故所求球的半径
.故所求球的半径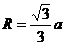 ,球的体积
,球的体积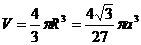 .
.
热点题型3
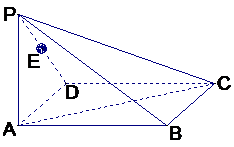 例3、如图,在四棱锥P-ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=
例3、如图,在四棱锥P-ABC右,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=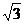 ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与P B所成角的余弦值;
B所成角的余弦值;
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离.
解法一:(Ⅰ)建立如图所示的空间直角坐标系,
则A、B、C、D、P、E的坐标分别为A(0,0,0),
B(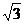 ,0,0),C(
,0,0),C(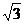 ,1,0),D(0,1,0),
,1,0),D(0,1,0),
P(0,0,2),E(0,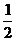 ,2).
,2).
从而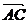 =(
=(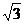 ,1,0),
,1,0),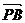 =(
=(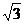 ,0,-2).
,0,-2).
设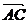 与
与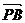 的夹角为
的夹角为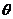 ,则
,则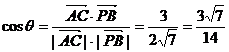 ,
,
∴AC与PB所成角的余弦值为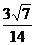 .
.
(Ⅱ)由于N点在侧面PAB内,故 可设N点
可设N点 坐标为(x,0,z),
坐标为(x,0,z),
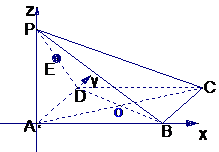 则
则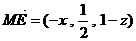 .由NE⊥面PAC可得:
.由NE⊥面PAC可得: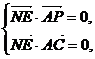 即
即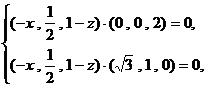
化简得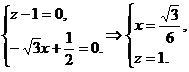
即N点的坐标为(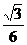 ,0,1),从而N点到AB、AP的距离分别为1,
,0,1),从而N点到AB、AP的距离分别为1,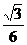

解法二:(Ⅰ)设AC∩BD=O,连OE,则OE//PB,
∴∠EOA即为AC与PB所成的角或其补角.
在ΔAOE中,AO=1,OE=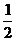 PB=
PB=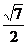 ,AE=
,AE=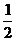 PD=
PD=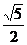 ,
,
∴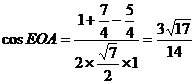 .
.
即AC与PB所成角的余弦值为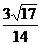 .
.
(Ⅱ)在面ABCD内过D作AC的垂线交AB于F,则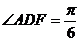 .
.
连PF,则在RtΔADF中DF=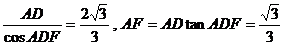 .
.
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC 从而NE⊥面PAC.
从而NE⊥面PAC.
∴N点到AB的距离=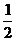 AP=1,N点到AP
AP=1,N点到AP 的距离=
的距离=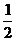 AF=
AF=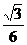 .
.
1.转化思想:将异面直线所成的角 ,直线与平面所成的角转化为平面角,然后解三角形;
,直线与平面所成的角转化为平面角,然后解三角形;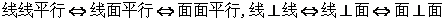
18.(14分)如图所示,光滑水平面的同一条直线上,有质量分别为mA=3m和mB=2m的小平板车A、B。质量为mC=m的物块C(可看作质点)放置在B车右端,物块C与B车上表面间的动摩擦因数是μ。开始时B车和物块C均静止,A车以初速度v0向右运动,在极短的时间内与B车发生弹性正碰。物块C最终恰好在B车中央停止相对滑动。重力加速度为g。求:
⑴A、B两车碰撞后瞬间,两车速度vA、vB的大小和方向;
⑵B车的长度l;
⑶物块C和B车刚好停止相对滑动的时刻,A车的右端和B车的左端间的距离d。
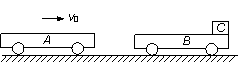
17.(14分)如图所示,P是倾角为30º的光滑固定斜面。劲度为k的轻弹簧一端固定在斜面底端的固定挡板C上,另一端与质量为m的物块A相连接。细绳的一端系在物体A上,细绳跨过不计质量和摩擦的定滑轮,另一端有一个不计质量的小挂钩。小挂钩不挂任何物体时,物体A处于静止状态,细绳与斜面平行。在小挂钩上轻轻挂上一个质量也为m的物块B后,物体A沿斜面向上运动。斜面足够长,运动过程中B始终未接触地面。
⑴求物块A刚开始运动时的加速度大小a;
⑵设物块A沿斜面上升通过Q点位置时速度最大,求该最大速度vm;
⑶若仅把物块B的质量改为2m,挂上B物块后,求A沿斜面上升到Q点位置时的速度v。

16.(12分)水平放置的固定平行板电容器,板间距离为d,两极板上各有一个小孔O1、O2,它们在同一竖直线上。一个质量为m的带电质点P从O1点正上方高d处,由静止开始自由下落,到达O1O2连线中点处速度恰好减小为零。重力加速度为g。
⑴求带电质点P在电场中受到的电场力大小F;
⑵为使带电质点恰好能到达小孔O2,它应从O1点正上方多高处开始自由下落?
⑶在满足第⑵问的情况下,该带电质点下落过程受到的电场力的冲量I的大小。

15.(12分)在月球表面上做平抛实验,从离月球表面高h处,将一小球以初速度v平抛,落到月球表面时的水平位移是2h。
⑴求该小球落到月球表面时的瞬时速度方向与月球表面的夹角θ;
⑵月球表面的重力加速度的大小g;
⑶已知嫦娥一号绕月球做匀速圆周运动时离月球表面的高度是月球半径的八分之一,求嫦娥一号绕月球做圆周运动的向心加速度大小a。
14.(10分)光滑水平地面上有两个质量分别为3m和2m的物体A、B,它们在同一直线上相向运动,速率依次为2v和v。已知发生正碰后其中一个物体恰好停止运动。求:
⑴恰好停止运动的是哪个物体?
⑵另一个物体碰后的速率是多大?
⑶碰撞过程中A、B系统损失的机械能是多少?
13.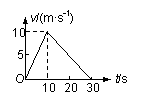 (10分)水平地面上静止有一个质量为m=4.0kg的物体,该物体在大小为F水平拉力的作用下开始运动。10s后水平拉力方向不变,大小突然减小为F/3。该物体的v-t图象如图所示。取g=10m/s2。求:
(10分)水平地面上静止有一个质量为m=4.0kg的物体,该物体在大小为F水平拉力的作用下开始运动。10s后水平拉力方向不变,大小突然减小为F/3。该物体的v-t图象如图所示。取g=10m/s2。求:
⑴物体在该运动过程的总位移是多大?
⑵开始阶段物体受到的水平拉力F的大小;
⑶物体与水平地面间的动摩擦因数μ。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com