
22.解:(Ⅰ)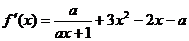
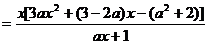
∵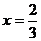 为
为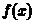 的极值点,∴
的极值点,∴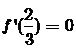
∴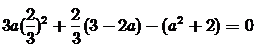 且
且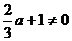
∴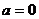 .
.
又当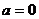 时,
时,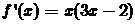 ,从而
,从而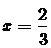 为
为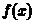 的极值点成立。
的极值点成立。
--------4分
(Ⅱ)因为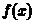 在
在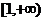 上为增函数,
上为增函数,
所以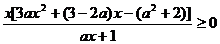 在
在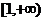 上恒成立. --------6分
上恒成立. --------6分
若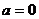 ,则
,则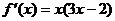 ,
,
∴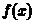 在
在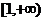 上为增函数不成立;
上为增函数不成立;
若 ,由
,由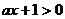 对
对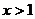 恒成立知
恒成立知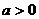 。
。
所以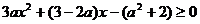 对
对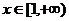 上恒成立。
上恒成立。
令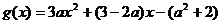 ,其对称轴为
,其对称轴为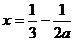 ,
,
因为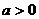 ,所以
,所以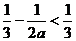 ,从而
,从而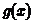 在
在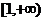 上为增函数。
上为增函数。
所以只要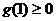 即可,即
即可,即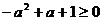
所以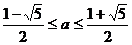
又因为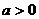 ,所以
,所以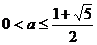 .
--------10分
.
--------10分
(Ⅲ)若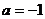 时,方程
时,方程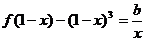
可得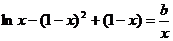
即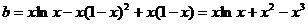 在
在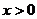 上有解
上有解
即求函数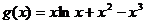 的值域.
的值域.
法一: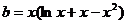
令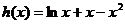
由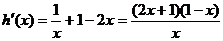
∵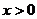
∴当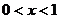 时,
时,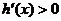 ,从而
,从而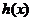 在(0,1)上为增函数;
在(0,1)上为增函数;
当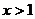 时,
时,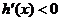 ,从而
,从而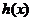 在(1,+∞)上为减函数。
在(1,+∞)上为减函数。
∴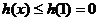 ,而
,而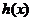 可以无穷小。
可以无穷小。
∴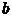 的取值范围为
的取值范围为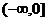 .
--------15分
.
--------15分
法二: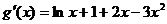
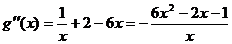
当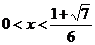 时,
时,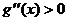 ,所以
,所以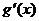 在
在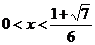 上递增;
上递增;
当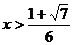 时,
时,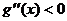 ,所以
,所以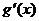 在
在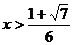 上递减;
上递减;
又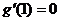 ,∴令
,∴令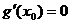 ,
,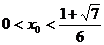 .
.
∴当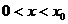 时,
时,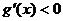 ,所以
,所以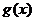 在
在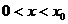 上递减;
上递减;
当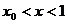 时,
时,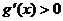 ,所以
,所以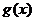 在
在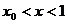 上递增;
上递增;
当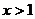 时,
时,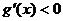 ,所以
,所以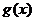 在
在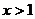 上递减;
上递减;
又当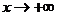 时,
时,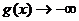 ,
,
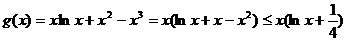
当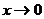 时,
时, 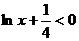 ,则
,则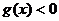 ,且
,且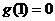
所以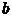 的取值范围为
的取值范围为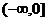 . --------15分
. --------15分
21.解:(Ⅰ)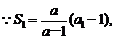 ∴
∴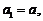
当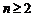 时,
时,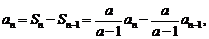
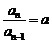 ,即
,即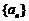 是等比数列. ∴
是等比数列. ∴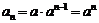 ;
……………………4分
;
……………………4分
(Ⅱ)由(Ⅰ)知,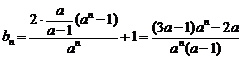 ,若
,若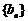 为等比数列,
为等比数列,
则有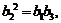 而
而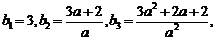
故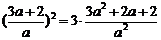 ,解得
,解得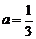 , ………………………………7分
, ………………………………7分
再将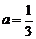 代入得
代入得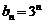 成立,
成立,
所以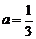 .
………………………………………………………………8分
.
………………………………………………………………8分
(III)证明:由(Ⅱ)知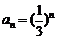 ,所以
,所以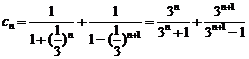
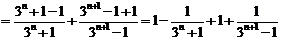
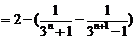 , ………………………………………………… 9分
, ………………………………………………… 9分
由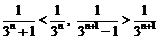 得
得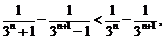
所以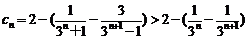 ,
…………………… 12分
,
…………………… 12分
从而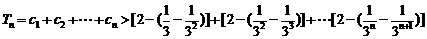
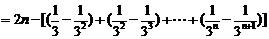
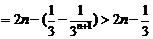 .
.
即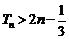 .
…………………………15分
.
…………………………15分
20.解:(1)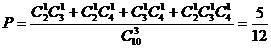 --------4分
--------4分
(2)x可能取的所有值有2,3,4 --------5分
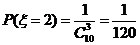
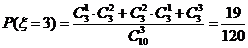
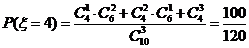 --------8分
--------8分
∴x的分布列为:
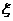
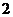
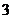
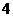
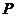
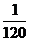
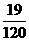
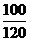
∴Ex=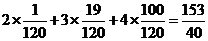 --------10分
--------10分
(3)当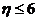 时,取出的3张卡片上的数字为1,2,2或1,2,3
时,取出的3张卡片上的数字为1,2,2或1,2,3
当取出的卡片上的数字为1,2,2或1,2,3的概率为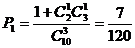 ,
,
∴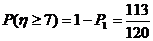 --------14分
--------14分
18.解:(Ⅰ)由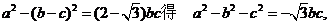
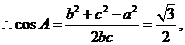
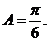 ---------4分
---------4分
由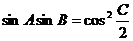 ,得
,得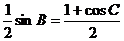
即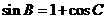
则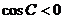 ,即
,即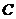 为钝角,故
为钝角,故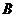 为锐角,且
为锐角,且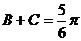
则
故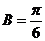 .
---------8分
.
---------8分
(Ⅱ)设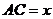 ,
,
由余弦定理得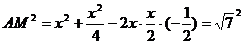
解得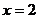
故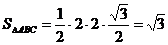 .
---------14分
.
---------14分
19解:(1)∵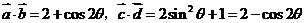 ,∴
,∴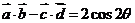 ,
,
∵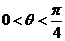 ,∴
,∴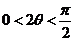 ,∴
,∴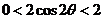 ,
,
∴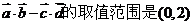 。
。
(2)∵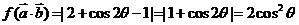 ,
,
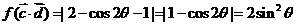 ,
,
∴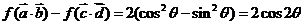 ,
,
∵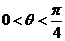 ,∴
,∴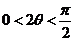 ,∴
,∴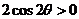 ,∴
,∴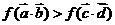
17、 1:(-6):5:(-8)
16、 ①②③
15. 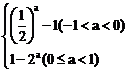
14. 6/5
13.
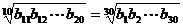
12、 168
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com