1、地位：兵家必争

虽然近年来立体几何试题在命题思路和方法上不时有些出人意外之处，但总体上还是保持了稳定，所以复习备考工作有章可循，有法可依。特别是立体几何试题难度中等，大题分步设问，层次分明，使得不同层次的学生都可得到一定的分数，因而立体几何成为历年数学高考中的“兵家必争之地”。

4、空间向量的应用

①理解直线的方向向量与平面的法向量。

②能用向量语言表述直线与直线、直线与平面、平面与平面的垂直、平行关系。

③能用向量方法证明有关直线和平面位置关系的一些定理(包括三垂线定理)。

④能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题，了解向量方法在研究几何问题中的作用。

3、空间向量及其运算

①了解空间向量的概念，了解空间向量的基本定理及其意义，掌握空间向量的正交分解及其坐标表示。

②掌握空间向量的线性运算及其坐标表示。

③掌握空间向量的数量积及其坐标表示，能运用向量的数量积判断向量的共线与垂直。

2、点、线、面之间的位置关系

①理解空间直线、平面位置关系的定义，并了解可以作为推理依据的公理(1、2、3、4)和定理(空间两角相等或互补)。

②以立体几何的上述定义、公理和定理为出发点，认识和理解空间中线面平行、垂直的有关性质与判定。

③能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题。

1、空间几何体

①认识柱、锥、台、球及其简单组合体的结构特征。

②能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述的三视图所表示立体模型，会用斜二测画法画出它们的直观图。

③会用平行投影与中心投影两种方法，画出简单空间图形的三视图与直观图，了解空间图形的不同表示形式。

④画出某些建筑物的视图与直观图(在不影响图形特征的基础上，尺寸、线条等不作严格要求)。

⑤了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式)。

30．读下列材料，完成下列问题。

材料一：某学校地理兴趣小组做了海陆昼夜增温、冷却的模拟实验，如左图所示：

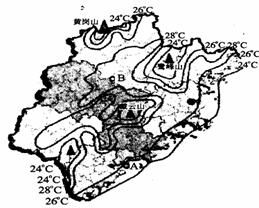
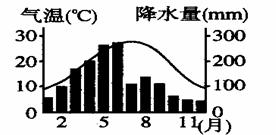材料二：下图中左图为“福建省7月气温分布图”，右图为左图中B地年内各月气温和降水量分布。

⑴材料一实验说明了什么地理原理：　　　　　　　　　　　　　　　　　　　　 。

⑵说出左图中由A地经戴云山、B地到黄岗山一线的气温分布特点；并根据材料一的实验，说明A地气温比B地低的原因。

⑶福建省是我国森林覆盖率最高的重点林区，森林火灾的危险性很大。结合该省气候图分析，说出B地一年中森林防火的重点季节及理由。