
(Ⅰ)求f(x)在[-1, 1]上的解析式 (Ⅱ)证明f(x)在(-1, 0)上时减函数(Ⅲ)当λ取何值时, 不等式f(x)>λ在R上有解?解:(Ⅰ):当x∈(-1, 0)时, - x∈(0, 1). ∵当x∈(0, 1)时, f(x)=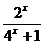 .
.
∴f(-x)=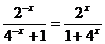 . 又f(x)是奇函数, ∴f (-x)= - f (x)=
. 又f(x)是奇函数, ∴f (-x)= - f (x)= 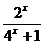 .∴f(x)= -
.∴f(x)= -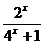 .
.
∵f(-0)= -f(0), ∴f(0)= 0. 又f(x)是最小正周期为2的函数, ∴对任意的x有f(x+2)= f(x).∴f(-1)= f(-1+2)= f(1). 另一面f(-1)=- f(1), ∴- f(1)= f(1) . ∴f(1) = f(-1)=0. ∴f(x)在[-1, 1]上的解析式为
f(x)=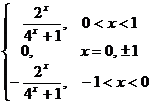 . (Ⅱ) 证明略; (Ⅲ) 不等式f(x)>λ在R上有解的λ的取值范围就是λ小于f(x)在R上的最大值. 当x∈(-1, 0)时,有-
. (Ⅱ) 证明略; (Ⅲ) 不等式f(x)>λ在R上有解的λ的取值范围就是λ小于f(x)在R上的最大值. 当x∈(-1, 0)时,有-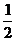 < f(x)= -
< f(x)= -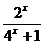 < -
< -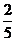 ;又f(x)是奇函数,当x∈(0, 1)时,f(x)在(0, 1)上也是减函数, ∴
;又f(x)是奇函数,当x∈(0, 1)时,f(x)在(0, 1)上也是减函数, ∴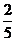 < f(x)=
< f(x)= 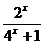 <
<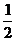 .. ∴f(x)在[-1, 1]上的值域是(-
.. ∴f(x)在[-1, 1]上的值域是(-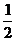 , -
, -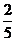 )∪{0}∪(
)∪{0}∪(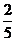 ,
, 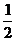 ). 由f(x)的周期是2;故f(x)在R上的值域是(-
). 由f(x)的周期是2;故f(x)在R上的值域是(-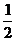 , -
, -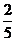 )∪{0}∪(
)∪{0}∪(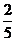 ,
, 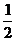 )
)
λ<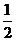 时,不等式f(x)>λ在R上有解.
时,不等式f(x)>λ在R上有解.
(2)在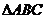 中,若
中,若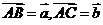 ,若P,Q,S为线段BC的四等分点,试证:
,若P,Q,S为线段BC的四等分点,试证: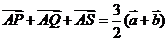 ;
;
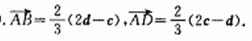 解:解:(1)由
解:解:(1)由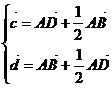 得
得
(2)证明:略
(2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?
解:(1)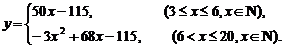 -------------------8分
-------------------8分
(2)当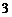 ≤
≤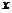 ≤6,且
≤6,且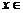 N时,∵
N时,∵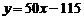 是增函数,∴当
是增函数,∴当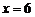 时,
时,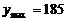 元.
元.
当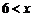 ≤20,
≤20,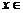 N时,
N时,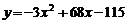
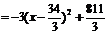 ,
,
∴当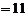 时,
时,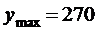 元.
元. 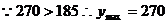 。
。
综上所述,当每辆自行车日租金定在11元时才能使日净收入最多,为270元.
(1)若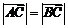 ,求
,求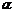 的值;(2)若
的值;(2)若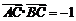 ,求
,求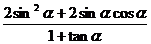 的值.
的值.
解:(1)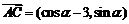 ,
,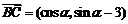 .
.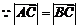 ,
,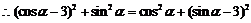 ,
,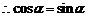 ,
,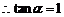 .
.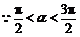 ,
,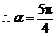 .
.
(2)由(1)知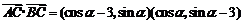 =
=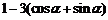 ,
,
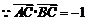 ,,
,,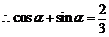 .平方,得
.平方,得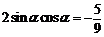 ,
,
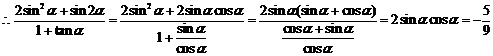
(1)求函数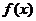 的最小正周期和图象的对称轴方程;(Ⅱ)求函数
的最小正周期和图象的对称轴方程;(Ⅱ)求函数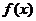 在区间
在区间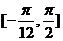 上的值域.
上的值域.
解:(1)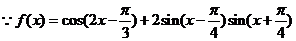
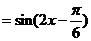
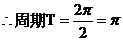 ,
,
由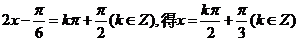
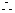 函数图象的对称轴方程为
函数图象的对称轴方程为 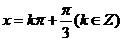
(2)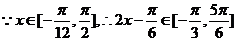 ; 因为
; 因为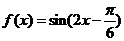 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,所以 函数的值域为
上单调递减,所以 函数的值域为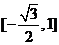
(2)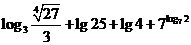 .解:(1)原式
.解:(1)原式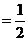 (2)原式
(2)原式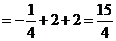
(2)已知集合 ,
,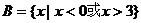 ,试分别求出满足下列条件的实数
,试分别求出满足下列条件的实数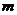 的取值范围.(Ⅰ)
的取值范围.(Ⅰ)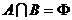 (Ⅱ)
(Ⅱ)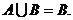
解:∵ ,∴
,∴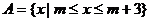 ,(1)当
,(1)当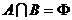 时,有
时,有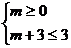 ,解得
,解得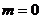
(2)当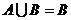 时,则
时,则 ,∴有
,∴有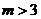 或
或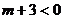 ,解得
,解得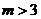 或
或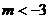
14. 解:(1)由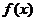 的定义可知,
的定义可知,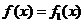 (对所有实数
(对所有实数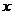 )等价于
)等价于
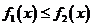 (对所有实数
(对所有实数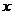 )这又等价于
)这又等价于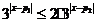 ,即
,即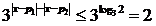 对所有实数
对所有实数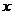 均成立. (*)由于
均成立. (*)由于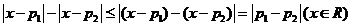 的最大值为
的最大值为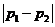 ,
,
故(*)等价于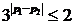 ,即
,即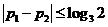 ,这就是所求的充分必要条件
,这就是所求的充分必要条件
(2)分两种情形讨论
(i)当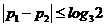 时,由(1)知
时,由(1)知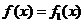 (对所有实数
(对所有实数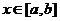 )
)
 则由
则由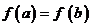 及
及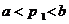 易知
易知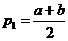 ,
,
再由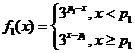 的单调性可知,
的单调性可知,
函数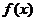 在区间
在区间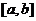 上的单调增区间的长度
上的单调增区间的长度
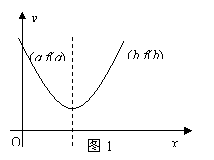
为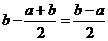 (参见示意图1)
(参见示意图1)
(ii)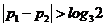 时,不妨设
时,不妨设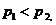 ,则
,则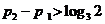 ,于是
,于是
当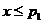 时,有
时,有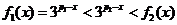 ,从而
,从而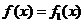 ;
;
当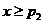 时,有
时,有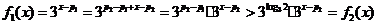 从而
从而 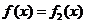 ;
;
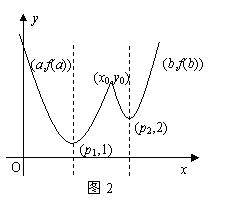 当
当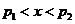 时,
时,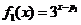 ,及
,及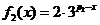 ,由方程
,由方程
得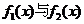 图象交点的横坐标为
图象交点的横坐标为
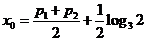 ⑴
⑴
显然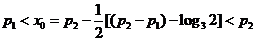 ,
,
这表明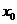 在
在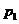 与
与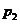 之间。由⑴易知
之间。由⑴易知
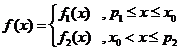
综上可知,在区间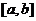 上,
上,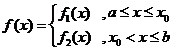 (参见示意图2)
(参见示意图2)
故由函数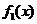 及
及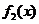 的单调性可知,
的单调性可知,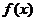 在区间
在区间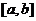 上的单调增区间的长度之和为
上的单调增区间的长度之和为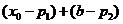 ,由于
,由于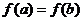 ,即
,即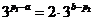 ,得
,得
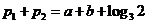 ⑵
⑵
故由⑴、⑵得 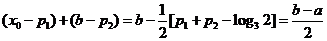
综合(i)(ii)可知,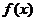 在区间
在区间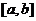 上的单调增区间的长度和为
上的单调增区间的长度和为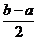 。
。
13. [解析]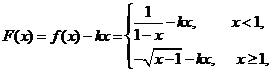
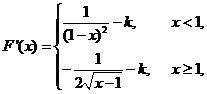
对于 ,当
,当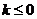 时,函数
时,函数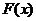 在
在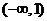 上是增函数;
上是增函数;
当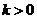 时,函数
时,函数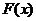 在
在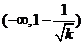 上是减函数,在
上是减函数,在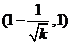 上是增函数;
上是增函数;
对于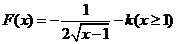 ,当
,当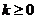 时,函数
时,函数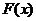 在
在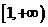 上是减函数;
上是减函数;
当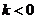 时,函数
时,函数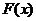 在
在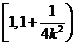 上是减函数,在
上是减函数,在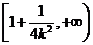 上是增函数。
上是增函数。
12. 解析:对于应付的电费应分二部分构成,高峰部分为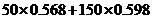 ;对于低峰部分为
;对于低峰部分为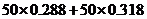 ,二部分之和为
,二部分之和为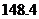
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com