
6、对函数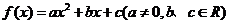 作
作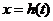 的代换,使得代换前后函数的值域总不改变的代换是
的代换,使得代换前后函数的值域总不改变的代换是
(1). h(t)=10t (2). h(t)=t2 (3). h(t)=2t (4). h(t)=log2t
5、定义在R上的函数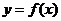 的值域为
的值域为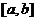 ,则
,则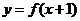 的值域为
的值域为
4、已知函数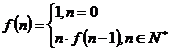 , 则
, 则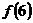 的值是
的值是
3、由“不超过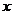 的最大整数”这一关系所确定的函数称为取整函数,通常记为
的最大整数”这一关系所确定的函数称为取整函数,通常记为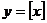 ,则函数
,则函数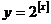 ,
,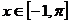 的值域为
的值域为
2、定义集合A、B的一种运算: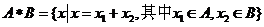 ,若
,若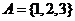 ,
,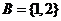 ,则
,则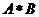 中的所有元素数字之和为
中的所有元素数字之和为
1、方程组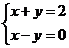 的解构成的集合是______________
的解构成的集合是______________
20. 20.解(1)因为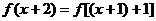
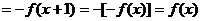
所以:2是函数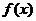 的一个周期……………………2分
的一个周期……………………2分
(2)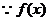 是以2为周期的函数,即
是以2为周期的函数,即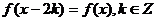
设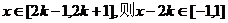
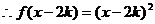 ,
,
即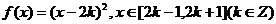 ………………6分
………………6分
(3)当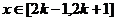 时,
时,
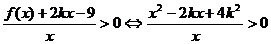
①当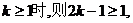
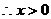
∴原题等价于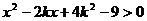 对任意
对任意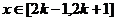 恒成立。
恒成立。
设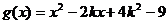
当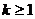 时,对称轴
时,对称轴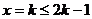
则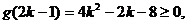
解得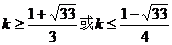
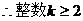 ……………………10分
……………………10分
②当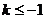 时,则
时,则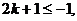
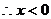 ∴原题等价于
∴原题等价于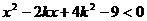 对任意
对任意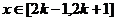 恒成立,
恒成立,
设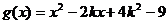
当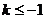 时,对称轴
时,对称轴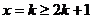
则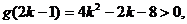
解得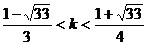
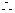 整数
整数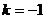 ……………………14分
……………………14分
③当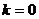 时,原命题等价于
时,原命题等价于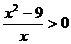 对任意
对任意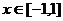 恒成立
恒成立
当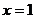 时,则
时,则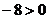 显然不成立
显然不成立
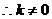 ……………………15分
……………………15分
综上所述,所求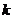 的取值范围是
的取值范围是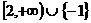 。---------------16分
。---------------16分
19. (1)假设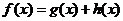 ①,其中
①,其中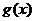 偶函数,
偶函数,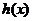 为奇函数,
为奇函数,
则有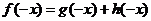 ,即
,即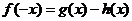 ②,
②,
由①、②解得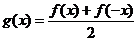 ,
,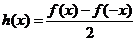 . …………2分
. …………2分
∵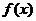 定义在R上,∴
定义在R上,∴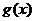 ,
,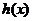 都定义在R上.
都定义在R上.
∵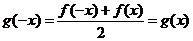 ,
,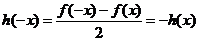 .
.
∴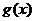 是偶函数,
是偶函数,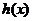 是奇函数,
是奇函数,
∵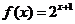 , ∴
, ∴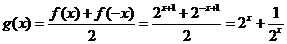 ,
,
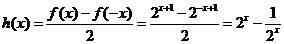 . …………6分
. …………6分
(2)由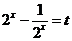 ,则
,则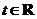 ,
,
平方得 ,∴
,∴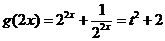 ,
,
∴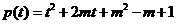 . …………10分
. …………10分
(3)∵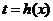 关于
关于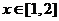 单调递增,∴
单调递增,∴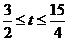 .…………12分
.…………12分
由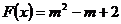 得
得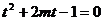
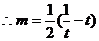 ,令
,令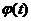 =
=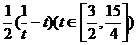
由题义得: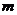 的取值范围就是函数
的取值范围就是函数 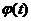 的值域。-----------14分
的值域。-----------14分
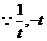 在
在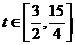 上均为减函数,
上均为减函数,
故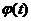 在
在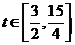 上单调递减,而
上单调递减,而
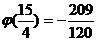
 函数
函数 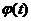 的值域为
的值域为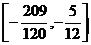
即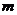 的取值范围为
的取值范围为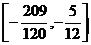 …………16分
…………16分
18. (2)试问日净收入最多时每辆自行车的日租金应定为多少元?日净收入最多为多少元?
解:(1)当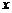 ≤6时,
≤6时,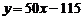 ,令
,令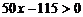 ,解得
,解得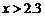 .
.
∵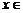 N,∴
N,∴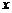 ≥3,∴
≥3,∴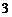 ≤
≤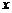 ≤6,且
≤6,且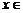 N.
-----------4分
N.
-----------4分
当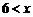 ≤20时,
≤20时,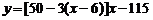
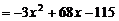 . ---------6分
. ---------6分
综上可知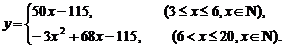 -------------------8分
-------------------8分
(2) 当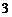 ≤
≤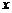 ≤6,且
≤6,且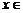 N时,∵
N时,∵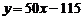 是增函数,
是增函数,
∴当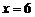 时,
时,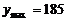 元.-----------------------------------------11分
元.-----------------------------------------11分
当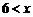 ≤20,
≤20,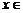 N时,
N时,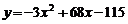
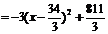 ,
,
∴当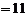 时,
时,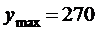 元.------------------------------------14分
元.------------------------------------14分
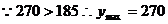 。
。
综上所述,当每辆自行车日租金定在11元时才能使日净收入最多,为270元.
---16分
9.2010
10. 6 11. 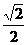 12. (3,1) 13. (3)(4) 14.
12. (3,1) 13. (3)(4) 14. 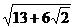
15. 解:(1)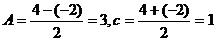
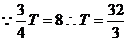
即 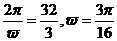 -
-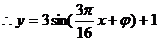 4分
4分
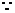
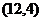 在函数图象上
在函数图象上
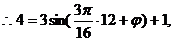 即
即
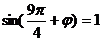
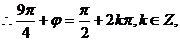 得
得
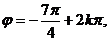
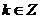
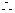 函数解析式为
函数解析式为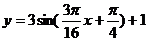 --
8分
--
8分
(2)先将函数的图像向左平移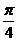 个单位,然后横坐标不变,纵坐标变为原来的3倍,再纵坐标不变,横坐标变为原来的
个单位,然后横坐标不变,纵坐标变为原来的3倍,再纵坐标不变,横坐标变为原来的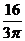 倍,最后向上平移1个单位。 14分
倍,最后向上平移1个单位。 14分
16.
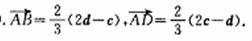 解:(1)由
解:(1)由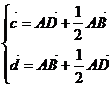 得
得
7分
(2)证明: 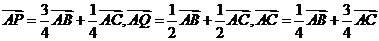
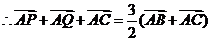 ,
,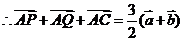 14分
14分
17. 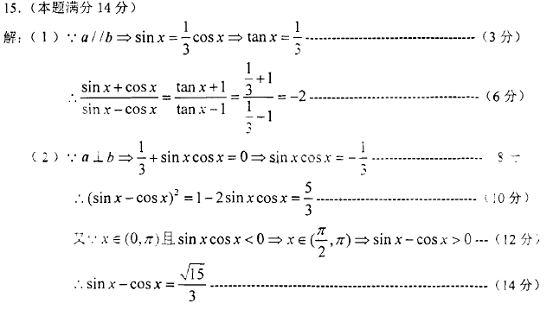
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com