
15.(2009江西卷理)如图,正四面体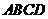 的顶点
的顶点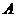 ,
,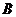 ,
,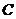 分别在两两垂直的三条射线
分别在两两垂直的三条射线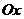 ,
,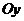 ,
,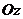 上,则在下列命题中,错误的为
上,则在下列命题中,错误的为
A.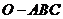 是正三棱锥
是正三棱锥
B.直线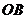 ∥平面
∥平面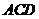
C.直线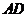 与
与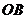 所成的角是
所成的角是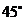
D.二面角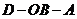 为
为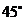
答案:B
[解析]将原图补为正方体不难得出B为错误,故选B
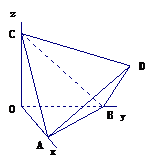
14. (2009江西卷文)如图,在四面体
(2009江西卷文)如图,在四面体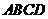 中,截面
中,截面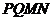 是正方形,则在下列命题中,错误的为
是正方形,则在下列命题中,错误的为
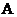 .
. 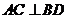
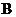 .
. 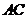 ∥截面
∥截面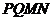
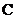 .
. 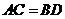
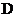 . 异面直线
. 异面直线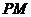 与
与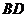 所成的角为
所成的角为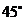
答案:C
[解析]由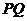 ∥
∥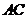 ,
,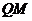 ∥
∥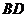 ,
,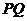 ⊥
⊥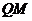 可得
可得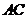 ⊥
⊥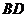 ,故
,故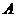 正确;由
正确;由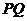 ∥
∥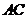 可得
可得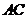 ∥截面
∥截面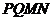 ,故
,故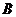 正确;
正确;
异面直线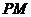 与
与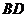 所成的角等于
所成的角等于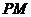 与
与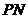 所成的角,故
所成的角,故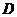 正确;
正确;
综上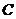 是错误的,故选
是错误的,故选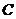 .
.
13.(2009全国卷Ⅰ理)已知二面角α-l-β为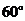 ,动点P、Q分别在面α、β内,P到β的距离为
,动点P、Q分别在面α、β内,P到β的距离为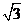 ,Q到α的距离为
,Q到α的距离为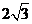 ,则P、Q两点之间距离的最小值为( C )
,则P、Q两点之间距离的最小值为( C )
(A) (B)2
(C)
(B)2
(C) 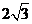 (D)4
(D)4
解:如图分别作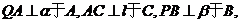
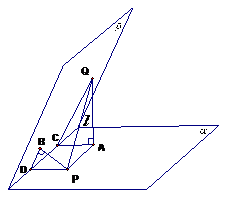
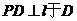 ,连
,连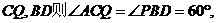
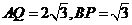 ,
,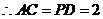
又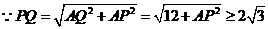
当且仅当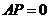 ,即
,即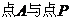 重合时取最小值。
重合时取最小值。
故答案选C。
12.(2009全国卷Ⅰ理)已知三棱柱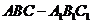 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,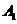 在底面
在底面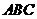 上的射影为
上的射影为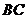 的中点,则异面直线
的中点,则异面直线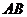 与
与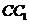 所成的角的余弦值为( D )
所成的角的余弦值为( D )
(A)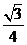 (B)
(B)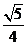 (C)
(C)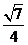 (D)
(D) 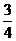
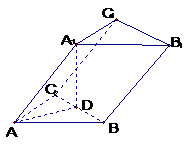
解:设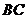 的中点为D,连结
的中点为D,连结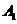 D,AD,易知
D,AD,易知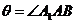 即为异面直线
即为异面直线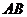 与
与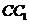 所成的角,由三角余弦定理,易知
所成的角,由三角余弦定理,易知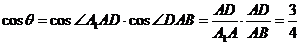 .故选D
.故选D
11.(2009全国卷Ⅱ文)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C。若圆C的面积等于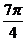 ,则球O的表面积等于
×
,则球O的表面积等于
×
答案:8π
解析:本题考查立体几何球面知识,注意结合平面几何知识进行运算,由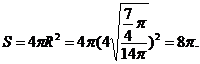
10.(2009全国卷Ⅱ文) 已知正四棱柱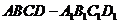 中,
中,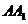 =
=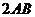 ,
,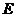 为
为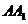 重点,则异面直线
重点,则异面直线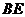 与
与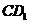 所形成角的余弦值为
所形成角的余弦值为
(A)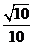 (B)
(B) 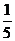 (C)
(C)
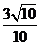 (D)
(D) 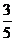
答案:C
解析:本题考查异面直线夹角求法,方法一:利用平移,CD’∥BA' ,因此求△EBA'中∠A'BE即可,易知EB=
,因此求△EBA'中∠A'BE即可,易知EB=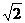 ,A'E=1,A'B=
,A'E=1,A'B=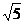 ,故由余弦定理求cos∠A'BE=
,故由余弦定理求cos∠A'BE=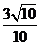 ,或由向量法可求。
,或由向量法可求。
9. (2009山东卷文)已知α,β表示两个不同的平面,m为平面α内的一条直线,则“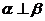 ”是“
”是“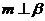 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
[解析]:由平面与平面垂直的判定定理知如果m为平面α内的一条直线,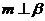 ,则
,则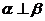 ,反过来则不一定.所以“
,反过来则不一定.所以“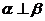 ”是“
”是“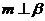 ”的必要不充分条件
”的必要不充分条件
答案:B.
[命题立意]:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.
8. (2009山东卷理)已知α,β表示两个不同的平面,m为平面α内的
一条直线,则“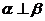 ”是“
”是“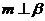 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
[解析]:由平面与平面垂直的判定定理知如果m为平面α内的
一条直线,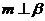 ,则
,则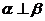 ,反过来则不一定.所以“
,反过来则不一定.所以“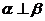 ”是“
”是“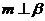 ”的必要不充分条件.
”的必要不充分条件.
答案:B.
[命题立意]:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.
7. (2009山东卷理)一空间几何体的三视图如图所示,则该几何体的体积为( ).
A.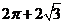 B.
B. 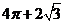 C.
C.
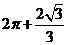 D.
D.
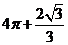
[解析]:该空间几何体为一圆柱和一四棱锥组成的,
圆柱的底面半径为1,高为2,体积为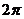 ,四棱锥的底面
,四棱锥的底面
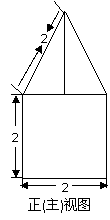
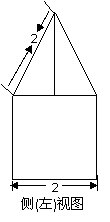 边长为
边长为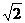 ,高为
,高为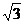 ,所以体积为
,所以体积为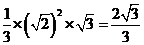
所以该几何体的体积为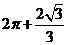 .
.
答案:C
[命题立意]:本题考查了立体几何中的空间想象能力,
由三视图能够想象得到空间的立体图,并能准确地
 计算出.几何体的体积.
计算出.几何体的体积.
6.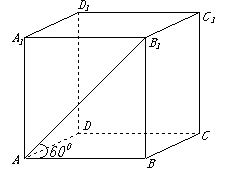 (2009北京卷理)若正四棱柱
(2009北京卷理)若正四棱柱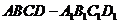 的底面边长为1,
的底面边长为1,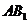 与底面
与底面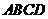 成60°角,则
成60°角,则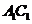 到底面
到底面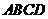 的距离为
( )
的距离为
( )
A.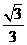 B.1
B.1
C.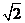 D.
D.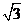
[答案]D
[解析]本题主要考查正四棱柱的概念、
直线与平面所成的角以及直线与平面的距离等概念. (第4题解答图)
属于基础知识、基本运算的考查.
依题意,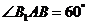 ,如图,
,如图,
 ,故选D.
,故选D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com