
22.已知F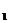 (-1, 0), F
(-1, 0), F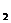 (1, 0), 点P满足|
(1, 0), 点P满足| |+|
|+|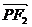 |=4
|=4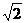 .
.
(1)写出点P的轨迹C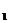 的方程;
的方程;
(2)曲线C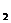 上点M满足: |MF
上点M满足: |MF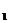 |=d+1, d表示M点到曲线C
|=d+1, d表示M点到曲线C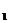 的左准线的距离, 过点F
的左准线的距离, 过点F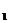 的直线L交曲线C
的直线L交曲线C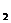 于A、B两点,
于A、B两点, 且△ABF
且△ABF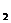 被x轴分成的两个三角形面积比
被x轴分成的两个三角形面积比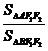 =
=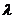 (
(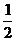 ≤
≤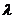 ≤3), 求直线L 的倾斜角的取值范围.
≤3), 求直线L 的倾斜角的取值范围.
21.设函数f(x)=(1+x)2-ln(1+x)2.
(1)若当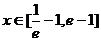 时,不等式f(x)>m恒成立,求实数m的取值范围;
时,不等式f(x)>m恒成立,求实数m的取值范围;
(2)若关于x的方程x2+x+a=f (x)在区间[0,2]上恰好有两个相异实根,求实数a的取值范围.
(x)在区间[0,2]上恰好有两个相异实根,求实数a的取值范围.
20.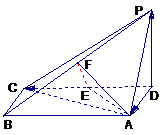 如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于
如图,四棱锥P-ABCD中,底面ABCD为矩形,PD垂直于
底面ABCD,AD=PD,E、F分别为CD、PB的中点.
(1)求证:EF垂直于平面PAB;
(2)设AB=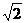 BC,求AC与平面A
BC,求AC与平面A EF所成的角的大小.
EF所成的角的大小.
19.在一次篮球练习课中,规定每人最多投篮5次,若投中2次就称为“通过”,若投中3次就称为“优秀”并停止投篮.已知甲每次投篮投中的概率是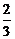 .
.
(1)求甲恰好投篮3次就通过的概率;
(2)设甲投篮投中的次数为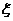 ,求随机变量
,求随机变量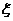 的分布列及数学期望E
的分布列及数学期望E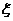 .
.
18.点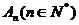 为抛物线
为抛物线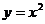 上横坐标为n的点,过点An作抛物线的切线
上横坐标为n的点,过点An作抛物线的切线 与x轴交于点Bn,设△OAnBn的面积为an(O为原点).
与x轴交于点Bn,设△OAnBn的面积为an(O为原点).
(1)求an;
(2)设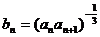 ,数列
,数列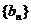 的前n项之和为
的前n项之和为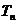 ,求证:
,求证: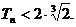
17.在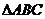 中,
中,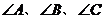 所对的边长分别为
所对的边长分别为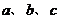 ,设
,设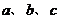 满足条件
满足条件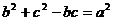 和
和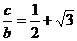 ,求
,求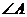 和
和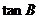 的值
的值
16.设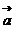 =(cosx-sinx, 2sinx),
=(cosx-sinx, 2sinx), 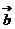 =(cosx+sinx, cosx), f(x)=
=(cosx+sinx, cosx), f(x)=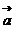 ·
·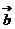 , 给出下列四个命题:
, 给出下列四个命题:
(1)
函数在区间[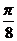 ,
,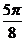 ]上是减函数;(2) 直线x=
]上是减函数;(2) 直线x=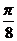 是函数图象的一条对称轴; (3) 函数f(x)的图像可由函数y=
是函数图象的一条对称轴; (3) 函数f(x)的图像可由函数y=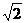 sin2x的图像按
sin2x的图像按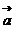 =(-
=(-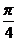 , 0)平移而得到;
, 0)平移而得到;
(4)
y=|f(x)|的最小正周期是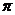 . 其中正确的命题序号是
.
. 其中正确的命题序号是
.
15.若不等式|x-1|<a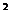 +a+1成立的充分条件是0<x<4, 则实数a的取值范围是 .
+a+1成立的充分条件是0<x<4, 则实数a的取值范围是 .
14.若双曲线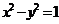 的右支上一点
的右支上一点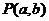 到直线
到直线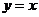 的距离为
的距离为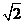 ,则
,则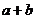 的值为 .
的值为 .
13.已知向量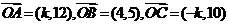 ,且A、B、C三点共线,则k= .
,且A、B、C三点共线,则k= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com