
19、多面体有关概念:(1)多面体:由若干个平面多边形围成的空间图形叫做多面体。围成多面体的各个多边形叫做多面体的面。多面体的相邻两个面的公共边叫做多面体的棱。(2)多面体的对角线:多面体中连结不在同一面上的两个顶点的线段叫做多面体的对角线。(3)凸多面体:把一个多面体的任一个面伸展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫做凸多面体。
18、空间距离的求法:(特别强调:立体几何中有关角和距离的计算,要遵循“一作,二证,三计算”的原则)
(1)异面直线的距离:①直接找公垂线段而求之;②转化为求直线到平面的距离,即过其中一条直线作平面和另一条直线平行。③转化为求平面到平面的距离,即过两直线分别作相互平行的两个平面。如已知正方体ABCD- A1B1C1D1的棱长为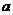 ,则异面直线BD与B1C的距离为_____(答:
,则异面直线BD与B1C的距离为_____(答: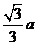 )。
)。
(2)点到直线的距离:一般用三垂线定理作出垂线再求解。如(1)等边三角形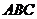 的边长为
的边长为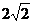 ,
, 是
是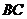 边上的高,将
边上的高,将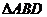 沿
沿 折起,使之与
折起,使之与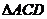 所在平面成
所在平面成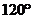 的二面角,这时
的二面角,这时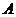 点到
点到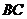 的距离是_____(答:
的距离是_____(答: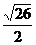 );(2)点P是120°的二面角α-
);(2)点P是120°的二面角α- -β内的一点,点P到α、β的距离分别是3、4,则P到
-β内的一点,点P到α、β的距离分别是3、4,则P到 的距离为 _______(答:
的距离为 _______(答: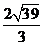 );(3)在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到棱A1B1与棱BC的距离相等,则动点P所在曲线的形状为_______(答:抛物线弧)。
);(3)在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到棱A1B1与棱BC的距离相等,则动点P所在曲线的形状为_______(答:抛物线弧)。
(3)点到平面的距离:①垂面法:借助于面面垂直的性质来作垂线,其中过已知点确定已知面的垂面是关键;②体积法:转化为求三棱锥的高;③等价转移法。如(1)长方体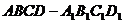 的棱
的棱 ,则点
,则点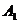 到平面
到平面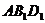 的距离等于______(答:
的距离等于______(答: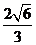 );(2)在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则A1到平面MBD的距离为______(答:a)。
);(2)在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则A1到平面MBD的距离为______(答:a)。
(4)直线与平面的距离:前提是直线与平面平行,利用直线上任意一点到平面的距离都相等,转化为求点到平面的距离。
(5)两平行平面之间的距离:转化为求点到平面的距离。
(6)球面距离(球面上经过两点的大圆在这两点间的一段劣弧的长度):求球面上两点A、B间的距离的步骤:①计算线段AB的长;②计算球心角∠AOB的弧度数;③用弧长公式计算劣弧AB的长。如(1)设地球半径为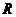 ,在北纬
,在北纬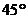 圈上有
圈上有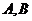 两地,它们的纬度圈上的弧长等于
两地,它们的纬度圈上的弧长等于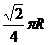 ,求
,求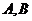 两地间的球面距离(答:
两地间的球面距离(答: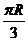 );(2)球面上有3点,其中任意两点的球面距离都等于大圆周长的
);(2)球面上有3点,其中任意两点的球面距离都等于大圆周长的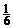 ,经过这3点的小圆的周长为
,经过这3点的小圆的周长为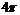 ,那么这个球的半径为______(答:
,那么这个球的半径为______(答: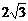 );(3)三棱锥
);(3)三棱锥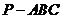 的三个侧面两两垂直,
的三个侧面两两垂直,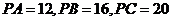 ,若
,若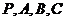 四个点都在同一球面上,则此球面上两点A、B之间的球面距离是_________(答:
四个点都在同一球面上,则此球面上两点A、B之间的球面距离是_________(答: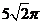 )。
)。
17、两个平面垂直的判定和性质:(1)判定:①判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。②定义法:即证两个相交平面所成的二面角为直二面角;(2)性质:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。如(1)三个平面两两垂直,它们的交线交于一点O,P到三个面的距离分别为3、4、5,则OP的长为_____(答:5);(2)在四棱锥P-ABCD中,PA⊥底面ABCD,底面各边都相等,M是PC上的一动点,当点M满足___________时,平面MBD⊥平面PCD(答: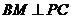 );(3)过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC。
);(3)过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC。
特别指出:立体几何中平行、垂直关系的证明的基本思路是利用线面关系的转化,即:

如(1)已知直线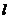
 平面
平面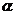 ,直线
,直线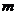
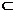 平面
平面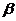 ,给出下列四个命题:①
,给出下列四个命题:①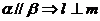
②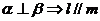 ;③
;③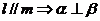 ;④
;④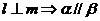 。其中正确的命题是_____(答:①③);(2)设
。其中正确的命题是_____(答:①③);(2)设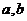 是两条不同直线,
是两条不同直线,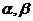 是两个不同平面,给出下列四个命题:①若
是两个不同平面,给出下列四个命题:①若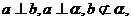 则
则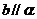 ;②若
;②若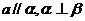 ,则
,则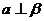 ;③若
;③若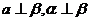 ,则
,则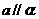 或
或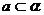 ;④若
;④若 则
则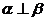 。其中正确的命题是_____(答:①③④)
。其中正确的命题是_____(答:①③④)
16、二面角:(1)平面角的三要素:①顶点在棱上;②角的两边分别在两个半平面内;③角的两边与棱都垂直。(2)作平面角的主要方法:①定义法:直接在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线,得出平面角,用定义法时,要认真观察图形的特性;②三垂线法:过其中一个面内一点作另一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;③垂面法:过一点作棱的垂面,则垂面与两个半平面的交线所成的角即为平面角;(3)二面角的范围: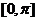 ;(4)二面角的求法:①转化为求平面角;②面积射影法:利用面积射影公式
;(4)二面角的求法:①转化为求平面角;②面积射影法:利用面积射影公式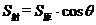 ,其中
,其中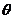 为平面角的大小。对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其可考虑面积射影法)。如(1)正方形ABCD-A1B1C1D1中,二面角B-A1C-A的大小为________(答:
为平面角的大小。对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其可考虑面积射影法)。如(1)正方形ABCD-A1B1C1D1中,二面角B-A1C-A的大小为________(答: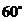 );(2)将∠A为60°的棱形ABCD沿对角线BD折叠,使A、C的距离等于BD,则二面角A-BD-C的余弦值是______(答:
);(2)将∠A为60°的棱形ABCD沿对角线BD折叠,使A、C的距离等于BD,则二面角A-BD-C的余弦值是______(答: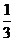 );(3)正四棱柱ABCD-A1B1C1D1中对角线BD1=8,BD1与侧面B1BCC1所成的为30°,则二面角C1-BD1-B1的大小为______(答:
);(3)正四棱柱ABCD-A1B1C1D1中对角线BD1=8,BD1与侧面B1BCC1所成的为30°,则二面角C1-BD1-B1的大小为______(答: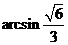 );(4)从点P出发引三条射线PA、PB、PC,每两条的夹角都是60°,则二面角B-PA-C的余弦值是______(答:
);(4)从点P出发引三条射线PA、PB、PC,每两条的夹角都是60°,则二面角B-PA-C的余弦值是______(答: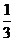 );(5)二面角α-
);(5)二面角α- -β的平面角为120°,A、B∈
-β的平面角为120°,A、B∈ ,AC
,AC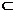 α,BD
α,BD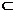 β,AC⊥
β,AC⊥ ,BD⊥
,BD⊥ ,若AB=AC=BD=1,则CD的长______(答:2);(6)ABCD为菱形,∠DAB=60°,PD⊥面ABCD,且PD=AD,则面PAB与面PCD所成的锐二面角的大小为______(答:
,若AB=AC=BD=1,则CD的长______(答:2);(6)ABCD为菱形,∠DAB=60°,PD⊥面ABCD,且PD=AD,则面PAB与面PCD所成的锐二面角的大小为______(答: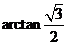 )。
)。
15、两个平面平行的判定和性质:(1)判定:一个如果平面内有两条相交直线和另一个平面平行,则这两个平面平行。(2)性质:如果两个平行平面同时与第三个平面相交,那么它们的交线平行。如(1)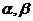 是两个不重合的平面,在下列条件中,不能判定平面
是两个不重合的平面,在下列条件中,不能判定平面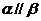 的条件是A、
的条件是A、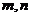 是
是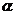 内一个三角形的两条边,且
内一个三角形的两条边,且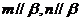 B、
B、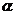 内有不共线的三点到
内有不共线的三点到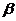 的距离都相等 C、
的距离都相等 C、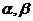 都垂直于同一条直线
都垂直于同一条直线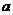 D、
D、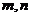 是两条异面直线,
是两条异面直线,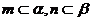 ,且
,且 (答:B);(2)给出以下六个命题:①垂直于同一直线的两个平面平行;②平行于同一直线的两个平面平行;③平行于同一平面的两个平面平行;④与同一直线成等角的两个平面平行;⑤一个平面内的两条相交直线于另一个平面内的两条相交直线平行,则这两个平面平行;⑥两个平面分别与第三个平面相交所得的两条交线平行,则这两个平面平行。其中正确的序号是___________(答:①③⑤);(3)正方体ABCD-A1B1C1D1中AB=
(答:B);(2)给出以下六个命题:①垂直于同一直线的两个平面平行;②平行于同一直线的两个平面平行;③平行于同一平面的两个平面平行;④与同一直线成等角的两个平面平行;⑤一个平面内的两条相交直线于另一个平面内的两条相交直线平行,则这两个平面平行;⑥两个平面分别与第三个平面相交所得的两条交线平行,则这两个平面平行。其中正确的序号是___________(答:①③⑤);(3)正方体ABCD-A1B1C1D1中AB=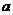 。①求证:平面AD1B1∥平面C1DB;②求证:A1C⊥平面AD1B1 ;③求平面AD1B1与平面C1DB间的距离(答:
。①求证:平面AD1B1∥平面C1DB;②求证:A1C⊥平面AD1B1 ;③求平面AD1B1与平面C1DB间的距离(答: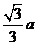 );
);
14、平面与平面的位置关系:(1)平行――没有公共点;(2)相交――有一条公共直线。
13、直线和平面所成的角:(1)定义:平面的一条斜线和它在平面内的射影所成的锐角,叫这条直线和这个平面所成的角。(2)范围: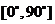 ;(3)求法:作出直线在平面上的射影;(4)斜线与平面所成的角的特征:斜线与平面中所有直线所成角中最小的角。如(1)在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,BD=1,则AD与平面AA1C1C所成的角为______(答:arcsin
;(3)求法:作出直线在平面上的射影;(4)斜线与平面所成的角的特征:斜线与平面中所有直线所成角中最小的角。如(1)在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,BD=1,则AD与平面AA1C1C所成的角为______(答:arcsin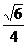 );(2)正方体ABCD-A1B1C1D1中,E、F分别是AB、C1D1的中点,则棱 A1B1 与截面A1ECF所成的角的余弦值是______(答:
);(2)正方体ABCD-A1B1C1D1中,E、F分别是AB、C1D1的中点,则棱 A1B1 与截面A1ECF所成的角的余弦值是______(答: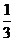 );(3)
);(3) 是从点
是从点 引出的三条射线,每两条的夹角都是
引出的三条射线,每两条的夹角都是 ,则直线
,则直线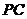 与平面
与平面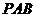 所成角的余弦值为______(答:
所成角的余弦值为______(答: );(4)若一平面与正方体的十二条棱所在直线都成相等的角θ,则sinθ的值为______(答:
);(4)若一平面与正方体的十二条棱所在直线都成相等的角θ,则sinθ的值为______(答: )。
)。
12、三垂线定理及逆定理:(1)定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。(2)逆定理:在平面内的一条直线,如果它和这个平面的一条斜线,那么它也和这条斜线在平面内的射影垂直。其作用是证两直线异面垂直和作二面角的平面角。
11、直线和平面垂直的判定和性质:(1)判定:①如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线和这个平面垂直。②两条平行线中有一条直线和一个平面垂直,那么另一条直线也和这个平面垂直。(2)性质:①如果一条直线和一个平面垂直,那么这条直线和这个平面内所有直线都垂直。②如果两条直线都垂直于同一个平面,那么这两条直线平行。如(1)如果命题“若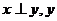 ∥z,则
∥z,则 ”不成立,那么字母x、y、z在空间所表示的几何图形一定是_____(答:x、y是直线,z是平面);(2)已知a,b,c是直线,α、β是平面,下列条件中能得出直线a⊥平面α的是 A、a⊥b,a⊥c其中b
”不成立,那么字母x、y、z在空间所表示的几何图形一定是_____(答:x、y是直线,z是平面);(2)已知a,b,c是直线,α、β是平面,下列条件中能得出直线a⊥平面α的是 A、a⊥b,a⊥c其中b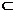 α,c
α,c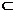 α B、a⊥b ,b∥α C、α⊥β,a∥β D、a∥b,b⊥α(答:D);(3)AB为⊙O的直径,C为⊙O上的一点,AD⊥面ABC,AE⊥BD于E,AF⊥CD于F,求证:BD⊥平面AEF。
α B、a⊥b ,b∥α C、α⊥β,a∥β D、a∥b,b⊥α(答:D);(3)AB为⊙O的直径,C为⊙O上的一点,AD⊥面ABC,AE⊥BD于E,AF⊥CD于F,求证:BD⊥平面AEF。
10、直线与平面平行的判定和性质:(1)判定:①判定定理:如果平面内一条直线和这个平面平面平行,那么这条直线和这个平面平行;②面面平行的性质:若两个平面平行,则其中一个平面内的任何直线与另一个平面平行。(2)性质:如果一条直线和一个平面平行,那么经过这条直线的平面和这个平面相交的交线和这条直线平行。在遇到线面平行时,常需作出过已知直线且与已知平面相交的辅助平面,以便运用线面平行的性质。如(1)α、β表示平面,a、b表示直线,则a∥α的一个充分不必要条件是 A、α⊥β,a⊥β B、α∩β=b,且a∥b C、a∥b且b∥α D、α∥β且a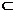 β(答:D);(2)正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥面AA1B1B。
β(答:D);(2)正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥面AA1B1B。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com