
17.(本小题满分13分)
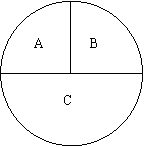 如图,一圆形靶分成A,B,C三部分,其面积之比为
如图,一圆形靶分成A,B,C三部分,其面积之比为
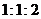 .某同学向该靶投掷
.某同学向该靶投掷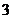 枚飞镖,每次1枚.假设他每
枚飞镖,每次1枚.假设他每
次投掷必定会中靶,且投中靶内各点是随机的.
(Ⅰ)求该同学在一次投掷中投中A区域的概率;
(Ⅱ)设X表示该同学在3次投掷中投中A区域的次数,求
X的分布列;
(Ⅲ)若该同学投中A,B,C三个区域分别可得3分,2分,
1分,求他投掷3次恰好得4分的概率.
16. (本小题满分14分)
(本小题满分14分)
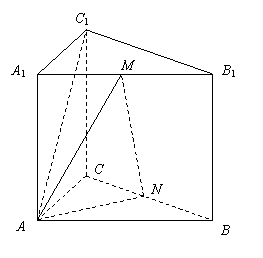
已知三棱柱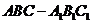 的侧棱垂直于底面,
的侧棱垂直于底面,
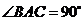 ,
,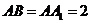 ,
,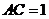 ,
,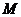 ,
,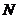
分别是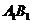 ,
,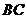 的中点.
的中点.
(Ⅰ)证明: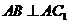 ;
;
(Ⅱ)证明: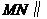 平面
平面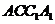 ;
;
(Ⅲ)求二面角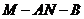 的余弦值.
的余弦值.
15.(本小题满分13分)
已知函数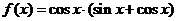 .
.
(Ⅰ)求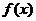 的最小正周期;
的最小正周期;
(Ⅱ)设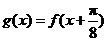 ,判断函数
,判断函数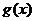 的奇偶性,并加以证明.
的奇偶性,并加以证明.
14. 在数列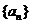 中,
中,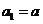 ,
,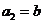 ,且
,且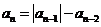 ,
,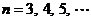 .
.
给出下列命题:
① 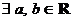 ,使得
,使得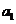 ,
,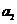 ,
,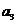 均为负数;
均为负数;
② 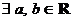 ,使得
,使得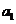 ,
,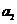 ,
,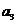 均为正数;
均为正数;
③ 若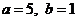 ,则
,则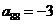 .
.
其中真命题的序号为___________.(填出所有真命题的序号)
13. 已知函数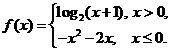 若函数
若函数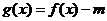
有3个零点,则实数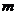 的取值范围是___________.
的取值范围是___________.
12. 如图,已知⊙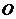 的直径
的直径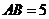 ,
,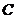 为圆周上一
为圆周上一
点,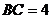 ,过点
,过点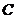 作⊙
作⊙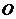 的切线
的切线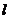 ,过点
,过点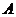 作
作
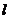 的垂线
的垂线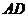 ,垂足为
,垂足为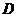 ,则
,则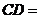 ___________.
___________.
11. △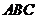 的内角
的内角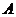 ,
,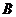 ,
,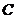 的对边分别为
的对边分别为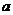 ,
,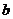 ,
,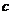 .若
.若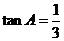 ,
,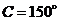 ,
,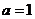 ,则
,则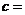
 ___________.
___________.
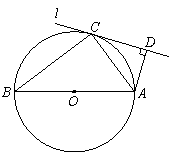
10. 已知向量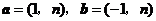 ,若
,若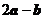 与
与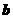 垂直,则
垂直,则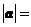 ___________.
___________.
9. 圆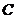 的极坐标方程
的极坐标方程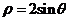 化成直角坐标方程为___________,半径长是
化成直角坐标方程为___________,半径长是
___________.
1.复数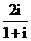 等于 等于 |
|||
(A)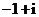 |
(B)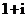 |
(C)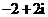 |
(D)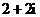 |
2.已知命题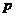 : :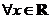 , ,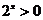 ,那么命题 ,那么命题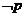 为 为 |
|||
(A)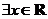 , ,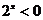 |
(B)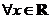 , ,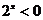 |
||
(C)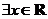 , ,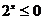 |
(D)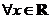 , ,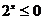 |
||
3.已知幂函数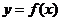 的图象经过点 的图象经过点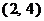 ,则 ,则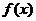 的解析式为 的解析式为 |
|||
(A)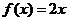 |
(B)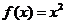 |
(C)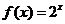 |
(D)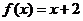 |
4.甲、乙两名同学在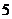 次数学考试中, 成绩统计用茎叶图表示如下. 若甲、乙两人的平均成绩分 次数学考试中, 成绩统计用茎叶图表示如下. 若甲、乙两人的平均成绩分别用 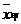 、 、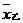 表示,则下列结论正确的是 表示,则下列结论正确的是 (A) (A)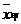 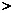 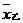 ,且甲比乙成绩稳定 ,且甲比乙成绩稳定(B) 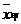 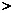 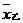 ,且乙比甲成绩稳定 ,且乙比甲成绩稳定(C) 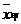 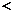 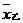 ,且甲比乙成绩稳定 ,且甲比乙成绩稳定  (D) (D)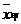 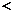 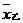 ,且乙比甲成绩稳定 ,且乙比甲成绩稳定 |
|||
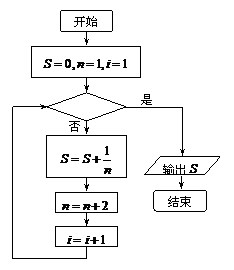 5.如图给出的是计算 5.如图给出的是计算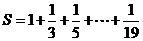 的值的 的值的一个程序框图,其中判断框内应填入的条件 是 (A) 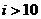 (B) 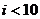 (C) 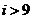 (D) 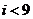 6.一个四棱锥的底面为正方形,其三视 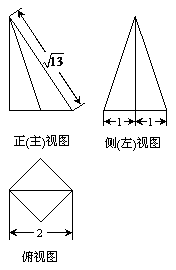 图如图所示,则这个四棱锥的体 图如图所示,则这个四棱锥的体积是 (A) 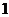 (B) 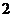 (C) 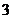 (D) 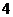 |
7.已知两点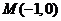 , ,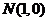 ,若直线 ,若直线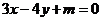 上存在点 上存在点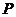 满足 满足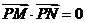 ,则实数 ,则实数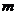 的取值范围是 的取值范围是 |
|||
(A)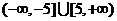 |
(B)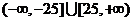 |
||
(C)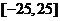 |
(D)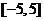 |
||
8.设集合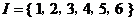 ,集合 ,集合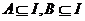 ,若 ,若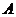 中含有3个元素, 中含有3个元素,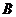 中至少含有2个元素,且 中至少含有2个元素,且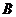 中所有数均不小于 中所有数均不小于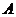 中最大的数,则满足条件的集合 中最大的数,则满足条件的集合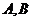 有 有 |
|||
|
(A)33组 |
(B)29组 |
(C)16组 |
(D)7组 |
第Ⅱ卷(非选择题 110分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com