10．[解析] (1)设雪橇运动的方向为正方向，狗第1次跳下雪橇后雪橇的速度为V₁，根据动量守恒定律，有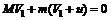

狗第1次跳上雪橇时，雪橇与狗的共同速度为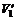满足

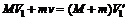
可解得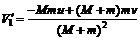

将u=－4m/s，v=5m/s，M=30kg，m=10kg代入，得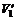=2m/s

(2)解法(一)

设雪橇运动的方向为正方向，狗第(n－1)次跳下雪橇后雪橇的速度为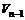，则狗第(n－1)次跳上雪橇后的速度为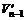满足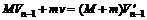

这样，狗n次跳下雪橇后，雪橇的速度为V_n，满足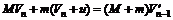

解得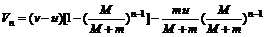

狗追不上雪橇的条件是V_n≥v

可化为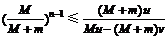

最后可求得n≥1+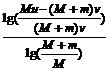

代入数据，得n≥3.41

狗最多能跳上雪橇3次．

雪橇最终的速度大小为V₄=5.625m/s

解法(二)：

设雪橇运动的方向为正方向，狗第i次跳下雪橇后，雪橇的速度为V_i，狗的速度为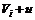；狗第i 次跳上雪橇后，雪橇和狗的共同速度为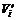，由动量守恒定律可得

第一次跳下雪橇：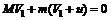

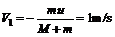
第一次跳上雪橇：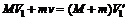

第二次跳下雪橇：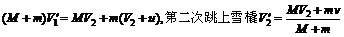

第三次跳下雪橇：，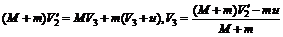

第三次跳上雪橇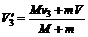

第四次跳下雪橇：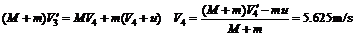

此进雪橇的速度已大于狗追赶的速度，狗将不可能追上雪橇．因此狗最多能跳上雪橇3次，雪橇最终的速度大小为5.625m/s．

9．[解析] (1)子弹做平抛运动，经时间t有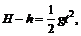解得t=0.6(s)．

此时子弹的速度与水平方向夹角为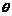，水平分速度为v_x、竖直分速度为 v_y，则有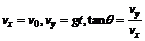

解得　　 ∴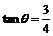

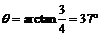
由于子弹沿斜面方向与木块相碰，故斜面的倾角与t s末子弹的速度与水平方向的夹角相同，所以斜面的倾角．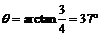

(2)设在C点子弹的末速度为v_t，则有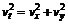

∴

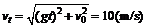
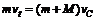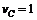子弹立即打入木块，满足动量守恒条件，有　　 解得(m/s)

碰后，子弹与木块共同运动由C点到与挡板碰撞并能够回到C点，

有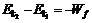

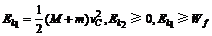
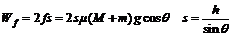
代入数据，得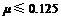

子弹与木块共同运动要能够回到C点，则斜面与塑料块间的动摩擦因数．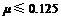

8．[解析] 以地面为参考系(下同)，设传送带的运动速度为v₀，在水平段运输的过程中，小货箱先在滑动摩擦力作用下做匀加速运动，设这段路程为s，所用时间为t；加速度为a，则对小箱有

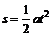　　　 ①

v₀=at　　 ②

在这段时间内，传送带运动的路程为s₀=v₀t　　　 ③

由以上可得s₀=2s　　 ④

用f 表示小箱与传送带之间的滑动摩擦力，则传送带对小箱做功为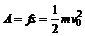　　 ⑤

传送带克服小箱对它的摩擦力做功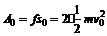　　 ⑥

两者之差就是克服摩擦力做功发出的热量　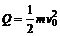 　　　⑦

可见，在小箱加速运动过程中，小箱获得的动能与发热量相等．

T时间内，电动机输出的功为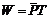　　 　⑧

此功用于增加小箱的动能、势能以克服摩擦力发热，

即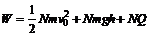　　 ⑨

已知相邻两小箱的距离为L，所以v₀T=NL　　 ⑩

联立⑦⑧⑨⑩，得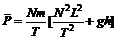　　 11

7．[解析] 物块的运动可分为以下四个阶段：①弹簧弹力做功阶段；②离开弹簧后在AB段的匀速直线运动阶段；③从B到C所进行的变速圆周运动阶段；④离开C点后进行的平抛运动阶段．弹簧弹力是变化的，求弹簧弹力的功可根据效果--在弹力作用下物块获得的机械能，即到达B点的动能求解．物块从B至C克服阻力做的功也是变力，同样只能根据B点和C点两点的机械能之差判断．因此求出物块在B点和C点的动能是关键．可根据题设条件：“进入导轨瞬间对导轨的压力为其重力的7倍”、“恰能到达C点”，求出．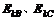

物块在B点时受力mg和导轨的支持力N=7mg，由牛顿第二定律，

有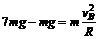

∴

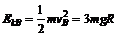
物块到达C点仅受重力mg，根据牛顿第二定律，有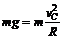

∴．

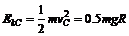(1)根据动能定理，可求得弹簧弹力对物体所做的功为W_弹=E_kB=3mgR．

(2)物体从B到C只有重力和阻力做功，根据动能定理，

有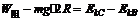

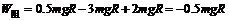
即物体从B到C克服阻力做的功为0.5mgR．

(3)物体离开轨道后做平抛运动，仅有重力做功，机械能守恒，

有．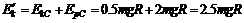

评析：中学阶段不要求直接用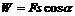求解变力做功，可根据其效果--使用能量变化间接来判断．对于物体运动的全过程必须逐段进行认真分析，确定每一阶段符合的规律：如本题最后一个阶段是平抛运动，物块在C点有动能，不能把平抛当成自由落体来处理．

6．[解析] (1)物体P从A下滑经B到C过程中根据动能定理：

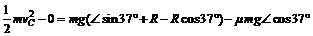
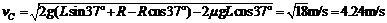
经C点时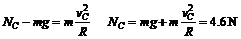

根据牛顿第三定律，P对C点的压力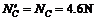

(2)从C到E机械能守恒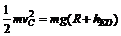

E与D间高度差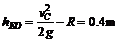

(3)物体P最后在B与其等高的圆弧轨道上来回运动时，经C点压力最小，由B到C根据机械能守恒

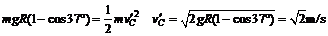
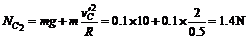
根据牛顿第三定律　 压力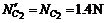

5．[解析] (1)设整个过程摩擦力做的功是W，由动能定理得：mgh－W=0　　 ①

W=mgh

(2)设物块沿轨道AB滑动的加速度为a₁，

由牛顿第二定律有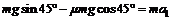　 ②

设物块到达B点时的速度为V_B，则有V_B=a₁t₁　 ③

设物块沿轨道BC滑动的加速度为a₂，由牛顿第二定律有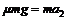　　 ④

物块从B点开始作匀减速运动，到达C点时，速度为零，故有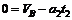　　 ⑤

由②③④⑤式可得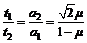：　　 ⑥

(3)使物块匀速地、缓慢地沿原路回到A点所需做的功应该是克服重力和阻力所做功之和，即是W₁=mgh+W=2mgh

4．[解析] 设离子喷出尾喷管时的速度为v，单位时间内喷出n个离子，则△t时间内喷出离子数为n△t，由动量定理得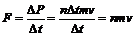

在发射离子过程中，卫星和发射出的离子系统，动量守恒，设喷出离子总质量为△m，则有△mv=(M－△m)v_星　 ∵△m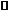m　 ∴v．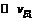

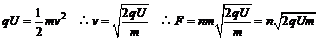
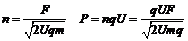
3．[解析] (1)物体由A滑到B的过程中，容器不脱离墙，物块由B沿球面向上滑时，物块对容器的作用力有一水平向右的分量，容器将脱离墙向右运动．因此，物块由A→B动量变化量最大，受容器的冲量最大，竖直墙作用于容器的冲量也最大．

物块由A→B机械能守恒，设物块滑到B的速度为v_B，则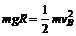

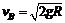∴　　 ①

物块动量变化量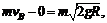方向沿水平方向．容器作用于物块的冲量为．

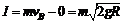容器不动，墙对容器的冲量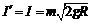，方向水平向右，这是最大冲量．

(2)物块从B处上升，容器向右运动过程中，系统水平方向动量守恒．物块上升到最高处相对容器静止的时刻，物块与容器具有共同的水平速度，设它为v，则由动量守恒定律得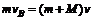　　 ②

系统机械能守恒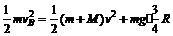　　 ③

联立①②③式解得　 M=3m

2．[答案] C

[解析] 无论子弹射入的深度如何，最终子弹和木块都等速，由动量守恒定律知，两种情况最终两木块(包括子弹)速度都相等．对木块由动能定理知：两次子弹对木块做功一样多．由动量定理知：两次木块所受冲量一样大．对系统由能的转化和守恒定律知，两次损失的机械能一样多，产生的热量也一样多．

1．[答案] D

[解析] 在△t₁时间内，I₁=F△t₁=mv=△p₁，在△t₂时间内．I₂=F△t₂=2mv－mv=mv=△p₂　 ∴I₁=I₂

又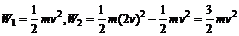

∴W₁<W₂，D选项正确．

[说明] 物体在恒定的合外力F作用下做直线运动，由牛顿第二定律可知物体做匀加速直线运动，速度由零增大到v的时间△t₂和由v增大到2v的时间△t₂是相等的，所以在△t₁和△t₂的两段时间内合外力的冲量是相等的．在△t₁的平均速度小于△t₂时间内的平均速度，从而得出在△t₁内的位移小于在△t­₂时间的位移，恒力F所做的功W₁<W₂．D选项正确．