
7、向量的运算律:(1)交换律: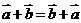 ,
,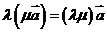 ,
,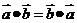 ;(2)结合律:
;(2)结合律: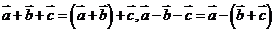 ,
,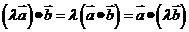 ;(3)分配律:
;(3)分配律: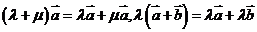 ,
,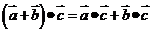 。如下列命题中:①
。如下列命题中:① 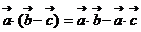 ;②
;② 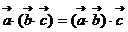 ;③
;③ 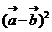
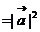
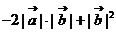 ;④ 若
;④ 若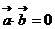 ,则
,则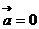 或
或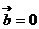 ;⑤若
;⑤若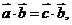 则
则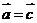 ;⑥
;⑥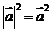 ;⑦
;⑦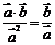 ;⑧
;⑧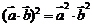 ;⑨
;⑨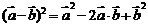 。其中正确的是______(答:①⑥⑨)
。其中正确的是______(答:①⑥⑨)
提醒:(1)向量运算和实数运算有类似的地方也有区别:对于一个向量等式,可以移项,两边平方、两边同乘以一个实数,两边同时取模,两边同乘以一个向量,但不能两边同除以一个向量,即两边不能约去一个向量,切记两向量不能相除(相约);(2)向量的“乘法”不满足结合律,即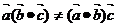 ,为什么?
,为什么?
6、向量的运算:
(1)几何运算:
①向量加法:利用“平行四边形法则”进行,但“平行四边形法则”只适用于不共线的向量,如此之外,向量加法还可利用“三角形法则”:设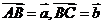 ,那么向量
,那么向量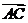 叫做
叫做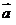 与
与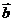 的和,即
的和,即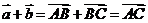 ;
;
②向量的减法:用“三角形法则”:设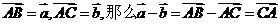 ,由减向量的终点指向被减向量的终点。注意:此处减向量与被减向量的起点相同。如(1)化简:①
,由减向量的终点指向被减向量的终点。注意:此处减向量与被减向量的起点相同。如(1)化简:①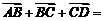 ___;②
___;②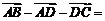 ____;③
____;③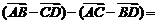 _____(答:①
_____(答:①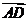 ;②
;②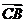 ;③
;③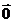 );(2)若正方形
);(2)若正方形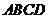 的边长为1,
的边长为1,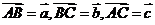 ,则
,则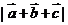 =_____(答:
=_____(答: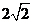 );(3)若O是
);(3)若O是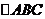 所在平面内一点,且满足
所在平面内一点,且满足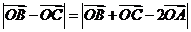 ,则
,则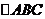 的形状为____(答:直角三角形);(4)若
的形状为____(答:直角三角形);(4)若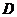 为
为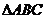 的边
的边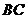 的中点,
的中点,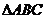 所在平面内有一点
所在平面内有一点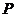 ,满足
,满足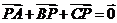 ,设
,设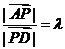 ,则
,则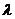 的值为___(答:2);(5)若点
的值为___(答:2);(5)若点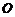 是
是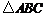 的外心,且
的外心,且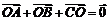 ,则
,则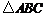 的内角
的内角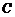 为____(答:
为____(答: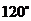 );
);
(2)坐标运算:设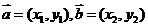 ,则:
,则:
①向量的加减法运算: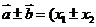 ,
,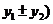 。如(1)已知点
。如(1)已知点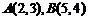 ,
,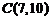 ,若
,若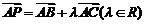 ,则当
,则当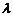 =____时,点P在第一、三象限的角平分线上(答:
=____时,点P在第一、三象限的角平分线上(答: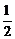 );(2)已知
);(2)已知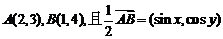 ,
,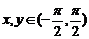 ,则
,则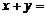 (答:
(答: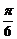 或
或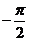 );(3)已知作用在点
);(3)已知作用在点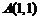 的三个力
的三个力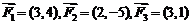 ,则合力
,则合力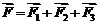 的终点坐标是 (答:(9,1))
的终点坐标是 (答:(9,1))
②实数与向量的积: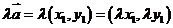 。
。
③若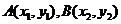 ,则
,则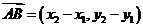 ,即一个向量的坐标等于表示这个向量的有向线段的终点坐标减去起点坐标。如设
,即一个向量的坐标等于表示这个向量的有向线段的终点坐标减去起点坐标。如设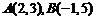 ,且
,且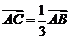 ,
,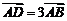 ,则C、D的坐标分别是__________(答:
,则C、D的坐标分别是__________(答: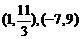 );
);
④平面向量数量积: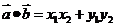 。如已知向量
。如已知向量 =(sinx,cosx),
=(sinx,cosx),  =(sinx,sinx),
=(sinx,sinx), 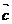 =(-1,0)。(1)若x=
=(-1,0)。(1)若x=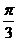 ,求向量
,求向量 、
、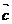 的夹角;(2)若x∈
的夹角;(2)若x∈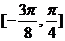 ,函数
,函数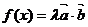 的最大值为
的最大值为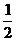 ,求
,求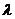 的值(答:
的值(答: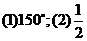 或
或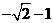 );
);
⑤向量的模: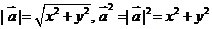 。如已知
。如已知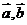 均为单位向量,它们的夹角为
均为单位向量,它们的夹角为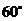 ,那么
,那么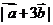 =_____(答:
=_____(答: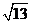 );
);
 ⑥两点间的距离:若
⑥两点间的距离:若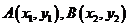 ,则
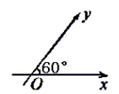
,则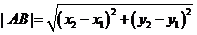 。如如图,在平面斜坐标系
。如如图,在平面斜坐标系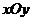 中,
中,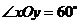 ,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若
,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若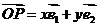 ,其中
,其中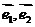 分别为与x轴、y轴同方向的单位向量,则P点斜坐标为
分别为与x轴、y轴同方向的单位向量,则P点斜坐标为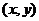 。(1)若点P的斜坐标为(2,-2),求P到O的距离|PO|;(2)求以O为圆心,1为半径的圆在斜坐标系
。(1)若点P的斜坐标为(2,-2),求P到O的距离|PO|;(2)求以O为圆心,1为半径的圆在斜坐标系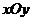 中的方程。(答:(1)2;(2)
中的方程。(答:(1)2;(2)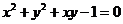 );
);
5、平面向量的数量积:
(1)两个向量的夹角:对于非零向量 ,
, ,作
,作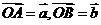 ,
,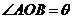
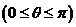 称为向量
称为向量 ,
, 的夹角,当
的夹角,当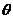 =0时,
=0时, ,
, 同向,当
同向,当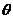 =
=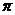 时,
时, ,
, 反向,当
反向,当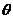 =
=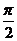 时,
时, ,
, 垂直。
垂直。
(2)平面向量的数量积:如果两个非零向量 ,
, ,它们的夹角为
,它们的夹角为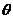 ,我们把数量
,我们把数量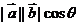 叫做
叫做 与
与 的数量积(或内积或点积),记作:
的数量积(或内积或点积),记作:
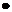
 ,即
,即
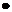
 =
=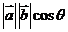 。规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。如(1)△ABC中,
。规定:零向量与任一向量的数量积是0,注意数量积是一个实数,不再是一个向量。如(1)△ABC中,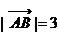 ,
,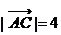 ,
,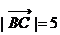 ,则
,则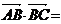 _________(答:-9);(2)已知
_________(答:-9);(2)已知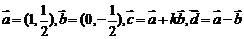 ,
,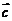 与
与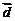 的夹角为
的夹角为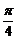 ,则
,则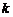 等于____(答:1);(3)已知
等于____(答:1);(3)已知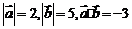 ,则
,则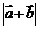 等于____(答:
等于____(答: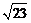 );(4)已知
);(4)已知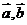 是两个非零向量,且
是两个非零向量,且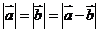 ,则
,则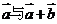 的夹角为____(答:
的夹角为____(答: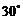 )
)
(3) 在
在 上的投影为
上的投影为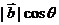 ,它是一个实数,但不一定大于0。如已知
,它是一个实数,但不一定大于0。如已知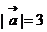 ,
,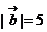 ,且
,且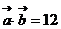 ,则向量
,则向量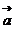 在向量
在向量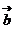 上的投影为______(答:
上的投影为______(答: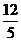 )
)
(4)
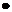
 的几何意义:数量积
的几何意义:数量积
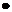
 等于
等于 的模
的模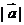 与
与 在
在 上的投影的积。
上的投影的积。
(5)向量数量积的性质:设两个非零向量 ,
, ,其夹角为
,其夹角为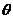 ,则:
,则:
①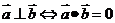 ;
;
②当 ,
, 同向时,
同向时,
 =
=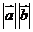 ,特别地,
,特别地,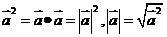 ;当
;当 与
与 反向时,
反向时,
 =-
=-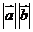 ;当
;当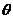 为锐角时,
为锐角时,
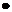
 >0,且
>0,且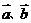 不同向,
不同向,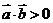 是
是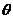 为锐角的必要非充分条件;当
为锐角的必要非充分条件;当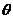 为钝角时,
为钝角时,
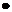
 <0,且
<0,且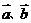 不反向,
不反向,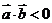 是
是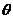 为钝角的必要非充分条件;
为钝角的必要非充分条件;
③非零向量 ,
, 夹角
夹角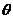 的计算公式:
的计算公式: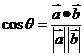 ;④
;④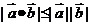 。如(1)已知
。如(1)已知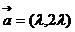 ,
,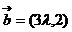 ,如果
,如果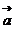 与
与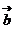 的夹角为锐角,则
的夹角为锐角,则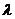 的取值范围是______(答:
的取值范围是______(答: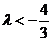 或
或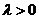 且
且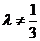 );(2)已知
);(2)已知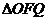 的面积为
的面积为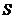 ,且
,且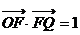 ,若
,若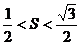 ,则
,则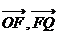 夹角
夹角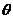 的取值范围是_________(答:
的取值范围是_________(答: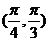 );(3)已知
);(3)已知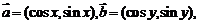
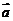 与
与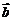 之间有关系式
之间有关系式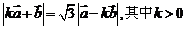 ,①用
,①用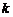 表示
表示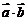 ;②求
;②求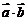 的最小值,并求此时
的最小值,并求此时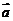 与
与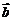 的夹角
的夹角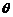 的大小(答:①
的大小(答:①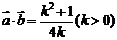 ;②最小值为
;②最小值为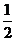 ,
,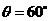 )
)
4、实数与向量的积:实数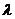 与向量
与向量 的积是一个向量,记作
的积是一个向量,记作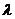
 ,它的长度和方向规定如下:
,它的长度和方向规定如下: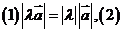 当
当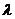 >0时,
>0时,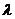
 的方向与
的方向与 的方向相同,当
的方向相同,当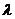 <0时,
<0时,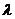
 的方向与
的方向与 的方向相反,当
的方向相反,当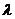 =0时,
=0时,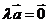 ,注意:
,注意: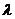
 ≠0。
≠0。
3.平面向量的基本定理:如果e1和e2是同一平面内的两个不共线向量,那么对该平面内的任一向量a,有且只有一对实数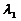 、
、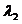 ,使a=
,使a=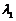 e1+
e1+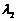 e2。如(1)若
e2。如(1)若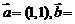
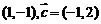 ,则
,则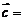 ______(答:
______(答: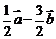 );(2)下列向量组中,能作为平面内所有向量基底的是 A.
);(2)下列向量组中,能作为平面内所有向量基底的是 A. 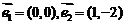 B.
B. 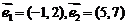 C.
C. 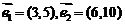 D.
D. 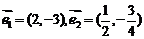 (答:B);(3)已知
(答:B);(3)已知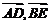 分别是
分别是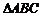 的边
的边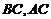 上的中线,且
上的中线,且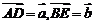 ,则
,则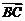 可用向量
可用向量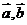 表示为_____(答:
表示为_____(答: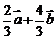 );(4)已知
);(4)已知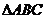 中,点
中,点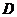 在
在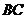 边上,且
边上,且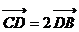 ,
,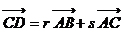 ,则
,则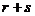 的值是___(答:0)
的值是___(答:0)
2、向量的表示方法:(1)几何表示法:用带箭头的有向线段表示,如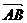 ,注意起点在前,终点在后;(2)符号表示法:用一个小写的英文字母来表示,如
,注意起点在前,终点在后;(2)符号表示法:用一个小写的英文字母来表示,如 ,
, ,
,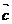 等;(3)坐标表示法:在平面内建立直角坐标系,以与
等;(3)坐标表示法:在平面内建立直角坐标系,以与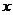 轴、
轴、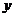 轴方向相同的两个单位向量
轴方向相同的两个单位向量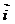 ,
,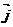 为基底,则平面内的任一向量
为基底,则平面内的任一向量 可表示为
可表示为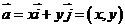 ,称
,称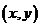 为向量
为向量 的坐标,
的坐标, =
=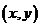 叫做向量
叫做向量 的坐标表示。如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。
的坐标表示。如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。
1、向量有关概念:
(1)向量的概念:既有大小又有方向的量,注意向量和数量的区别。向量常用有向线段来表示,注意不能说向量就是有向线段,为什么?(向量可以平移)。如已知A(1,2),B(4,2),则把向量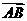 按向量
按向量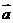 =(-1,3)平移后得到的向量是_____(答:(3,0))
=(-1,3)平移后得到的向量是_____(答:(3,0))
(2)零向量:长度为0的向量叫零向量,记作: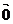 ,注意零向量的方向是任意的;
,注意零向量的方向是任意的;
(3)单位向量:长度为一个单位长度的向量叫做单位向量(与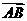 共线的单位向量是
共线的单位向量是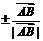 );
);
(4)相等向量:长度相等且方向相同的两个向量叫相等向量,相等向量有传递性;
(5)平行向量(也叫共线向量):方向相同或相反的非零向量 、
、 叫做平行向量,记作:
叫做平行向量,记作: ∥
∥ ,规定零向量和任何向量平行。提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有
,规定零向量和任何向量平行。提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有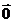 );④三点
);④三点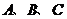 共线
共线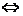
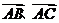 共线;
共线;
(6)相反向量:长度相等方向相反的向量叫做相反向量。 的相反向量是-
的相反向量是- 。
。
如下列命题:(1)若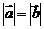 ,则
,则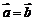 。(2)两个向量相等的充要条件是它们的起点相同,终点相同。(3)若
。(2)两个向量相等的充要条件是它们的起点相同,终点相同。(3)若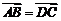 ,则
,则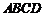 是平行四边形。(4)若
是平行四边形。(4)若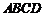 是平行四边形,则
是平行四边形,则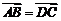 。(5)若
。(5)若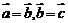 ,则
,则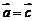 。(6)若
。(6)若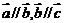 ,则
,则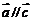 。其中正确的是_______(答:(4)(5))
。其中正确的是_______(答:(4)(5))
16.(2008·镇江) 如图6-48所示,在容器底部固定一轻质弹簧,弹簧上方连有长方体木块A,容器侧面的底部有一个由阀门B控制的出水口,当容器中水深为20cm时,木块A有2/5的体积浸在水中,此时弹簧恰好处于自然状态,没有发生形变.(不计弹簧受到的浮力,g取10N/kg) 。
(1)求此时容器底部受到的水的压强。
(2)求木块A的密度。
(3)向容器内缓慢加水,直至木块A刚好完全浸没水中,立即停止加水,此时弹簧对木块A 的作用力为F1,在原图上画出此时水面的大致位置。
(4)打开阀门B缓慢放水,直至木块A刚好完全离开水面时,立即关闭阀门B,此时弹簧对木块A的作用力为F2,求F1、F2之比。
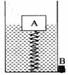 图6-48
图6-48
15.(2008·宜昌)图6-47是我国设计的北京202008年奥运会奖牌,奖牌正面为国际奥委会统一规定的图案,奖牌背面镶嵌着取自中国的玉石,形象诠释了中华民族自古以来以“玉”比“德”的价值观,是中华文明与奥林匹克精神的一次
“中西合璧”。奖牌分为金牌、银牌和铜牌。其中金牌由纯银、玉石、纯金组成,金牌的总体积约为23cm3,镶嵌玉石的体积约为5.4cm3,纯金的质量约为6g。(已知:ρ玉=3.0g/cm3,ρ金=19.3g/cm3,ρ银=10.5g/cm3)。请问:

图6-47
(1)一枚金牌约需要玉石多少克? (2)一枚金牌除了玉石和纯金外,还需纯银约多少克?(计算结果保留一位小数)
14.(2009·福建惠安)小刚想了解花生油的密度:
⑴ 小刚想,花生油是油类,它的密度应该比水小,于是他滴了一滴油在水中,发现油浮在水面上,由此可以证明他的猜想是________的.
(2)在调节天平平衡时发现指针指在分度盘如图6-44的位置,他应该将平衡螺母向
移动.

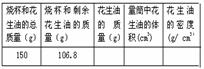
 (3)用天平测出烧杯和花生油的总质量为150g,然后将一部分花生油倒入量筒中,再测出剩余花生油和烧杯的质量为106.8g,读出量筒中花生油的体积,如图6-45所示,最后算出花生油的密度,请你将测得的结果填入下表.
(3)用天平测出烧杯和花生油的总质量为150g,然后将一部分花生油倒入量筒中,再测出剩余花生油和烧杯的质量为106.8g,读出量筒中花生油的体积,如图6-45所示,最后算出花生油的密度,请你将测得的结果填入下表.
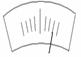
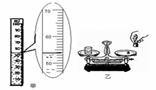
图6-44 图6-45 图6-46
(4)图6-46是他在实验结束后整理器材的情景,其中操作不规范的是___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com