
7.(2009福建文1)若集合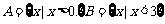 ,则
,则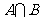 等于 ( )
等于 ( )
A.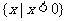 B.
B.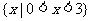 C.
C.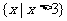 D.R
D.R
6.(2009辽宁文1)已知集合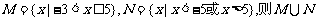 = ( )
= ( )
A. B.
B.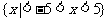
C.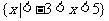 D.
D.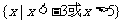
5.(2009海南宁夏文1)已知集合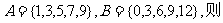
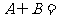 ( )
( )
(A)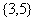 (B)
(B)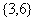
(C)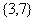 (D)
(D)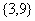
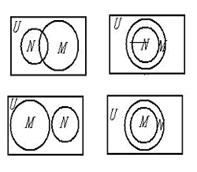
4.(2009广东文1)已知全集U=R,则正确表示集合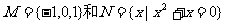 关系的韦恩
关系的韦恩
(Venn)图是 ( )
3.(2009安徽文2)若集合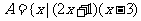
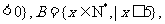 则
则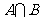 是 ( )
是 ( )
(A){1,2,3} (B){1,2}
(C){4,5} (D){1,2,3,4,5}
2.(2009天津文13)设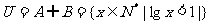
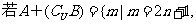
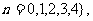 则集合B=______
则集合B=______
◆ 集合与集合的关系
1.(2008山东文1)满足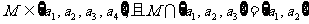 的集合M的个数是
( )
的集合M的个数是
( )
(A)1 (B)2
(C)3 (D)4
22.解:(Ⅰ)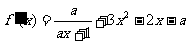
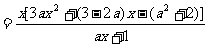
∵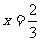 为
为 的极值点,∴
的极值点,∴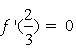
∴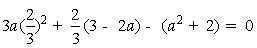 且
且
∴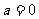 .
.
又当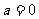 时,
时,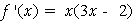 ,从而
,从而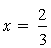 为
为 的极值点成立。
的极值点成立。
--------4分
(Ⅱ)因为 在
在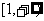 上为增函数,
上为增函数,
所以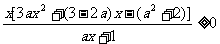 在
在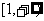 上恒成立. --------6分
上恒成立. --------6分
若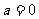 ,则
,则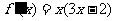 ,
,
∴ 在
在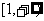 上为增函数不成立;
上为增函数不成立;
若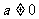 ,由
,由 对
对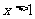 恒成立知
恒成立知 。
。
所以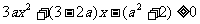 对
对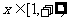 上恒成立。
上恒成立。
令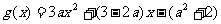 ,其对称轴为
,其对称轴为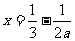 ,
,
因为 ,所以
,所以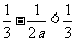 ,从而
,从而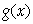 在
在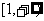 上为增函数。
上为增函数。
所以只要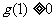 即可,即
即可,即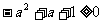
所以
又因为 ,所以
,所以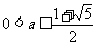 .
--------10分
.
--------10分
(Ⅲ)若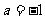 时,方程
时,方程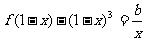
可得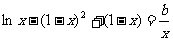
即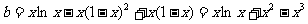 在
在 上有解
上有解
即求函数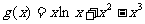 的值域.
的值域.
法一: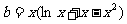
令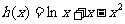
由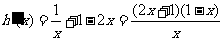
∵
∴当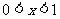 时,
时,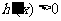 ,从而
,从而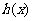 在(0,1)上为增函数;
在(0,1)上为增函数;
当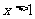 时,
时,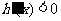 ,从而
,从而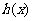 在(1,+∞)上为减函数。
在(1,+∞)上为减函数。
∴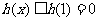 ,而
,而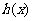 可以无穷小。
可以无穷小。
∴ 的取值范围为
的取值范围为 .
--------15分
.
--------15分
法二: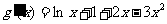

当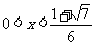 时,
时,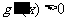 ,所以
,所以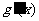 在
在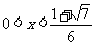 上递增;
上递增;
当 时,
时,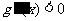 ,所以
,所以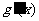 在
在 上递减;
上递减;
又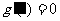 ,∴令
,∴令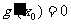 ,
,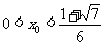 .
.
∴当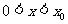 时,
时,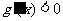 ,所以
,所以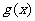 在
在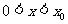 上递减;
上递减;
当 时,
时,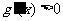 ,所以
,所以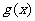 在
在 上递增;
上递增;
当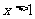 时,
时,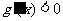 ,所以
,所以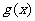 在
在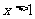 上递减;
上递减;
又当 时,
时,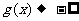 ,
,
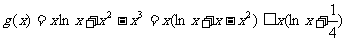
当 时,
时, 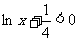 ,则
,则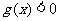 ,且
,且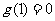
所以 的取值范围为
的取值范围为 . --------15分
. --------15分
22、(本小题15分)
已知函数 .
.
(Ⅰ) 若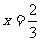 为
为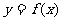 的极值点,求实数
的极值点,求实数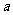 的值;
的值;
(Ⅱ) 若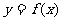 在
在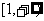 上为增函数,求实数
上为增函数,求实数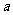 的取值范围;
的取值范围;
(Ⅲ) 若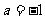 时,方程
时,方程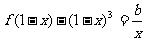 有实根,求实数
有实根,求实数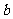 的取值范围.
的取值范围.
21.解:(Ⅰ)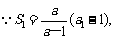 ∴
∴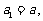
当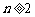 时,
时,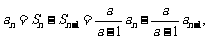
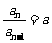 ,即
,即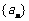 是等比数列. ∴
是等比数列. ∴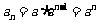 ;
……………………4分
;
……………………4分
(Ⅱ)由(Ⅰ)知,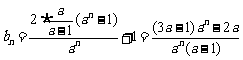 ,若
,若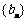 为等比数列,
为等比数列,
则有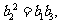 而
而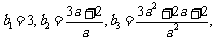
故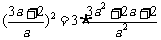 ,解得
,解得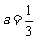 , ………………………………7分
, ………………………………7分
再将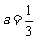 代入得
代入得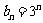 成立,
成立,
所以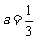 . ………………………………………………………………8分
. ………………………………………………………………8分
(III)证明:由(Ⅱ)知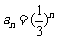 ,所以
,所以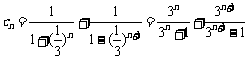
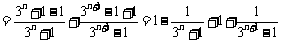
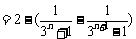 , ………………………………………………… 9分
, ………………………………………………… 9分
由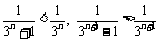 得
得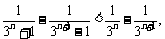
所以 , …………………… 12分
, …………………… 12分
从而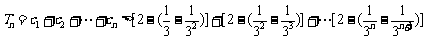
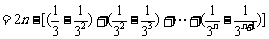
 .
.
即 .
…………………………15分
.
…………………………15分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com