
(一)知识体系
 表达方式--叙述(顺叙.倒叙.插叙).描写(语言描写.心理描写.外貌描写.行为描写.景物描写.环境描写).抒情(直接抒情.间接抒情).议论.说明
表达方式--叙述(顺叙.倒叙.插叙).描写(语言描写.心理描写.外貌描写.行为描写.景物描写.环境描写).抒情(直接抒情.间接抒情).议论.说明
表现手法--铺垫.烘托.对比.象征
布局谋篇--线索.顺序.过渡.照应.详略
 描绘类(生动形象):比喻.夸张.拟人
描绘类(生动形象):比喻.夸张.拟人
语言辞格 结构类(强调突出):对偶.排比.反复
语气类(增强语气):反问.设问
思想内容--人物形象.主题思想
涉及到写法的问题,还要注意:
(1)衬托:使用喻体反衬,表现情感更强烈。
(2)比喻:知道喻体追索本体,要联系上下文语境考查。
(3)对比:通过对比,反映出好几个方面,突出表现某些作用。
(4)排比:排比反复的好处是:层层铺开,逐步扩大,对点明主旨起强化作用。
(5)变换人称的写法:第二人称便于抒情,便于对话;用第三人称可以写不同人的感受,涉及的内容广泛。
20.设数列 的前
的前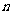 项和为
项和为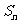 ,
,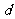 为常数,已知对
为常数,已知对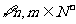 ,当
,当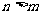 时,总有
时,总有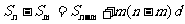
⑴ 求证:数列{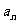 }是等差数列; ⑵ 若正整数n, m, k成等差数列,比较
}是等差数列; ⑵ 若正整数n, m, k成等差数列,比较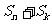 与
与 的大小,并说明理由!
的大小,并说明理由!
⑶ 探究 :  “对
“对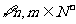 ,当
,当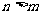 时,总有
时,总有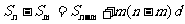 ”是
”是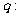 “数列{
“数列{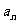 }是等差数列”的充要条件吗?并给出证明!由此类比,你能给出数列{
}是等差数列”的充要条件吗?并给出证明!由此类比,你能给出数列{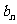 }是等比数列(公比为
}是等比数列(公比为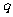 ,且
,且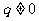 )的充要条件吗?
)的充要条件吗?
19.已知函数f(x)=x2-x+alnx
(1)当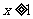 时,
时,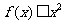 恒成立,求
恒成立,求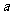 的取值范围; (2)讨论
的取值范围; (2)讨论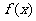 在定义域上的单调性;
在定义域上的单调性;
18.设数列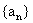 的各项都是正数, 且对任意
的各项都是正数, 且对任意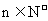 都有
都有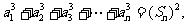 记
记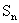 为数列
为数列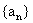 的前n项和
的前n项和
(1) 求证: 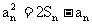 ;(2)
求数列
;(2)
求数列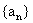 的通项公式;
的通项公式;
(3) 若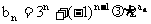 (
( 为非零常数,
为非零常数, 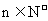 ), 问是否存在整数
), 问是否存在整数 , 使得对任意
, 使得对任意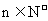 ,
,
都有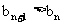

17.若存在实常数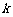 和
和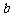 ,使得函数
,使得函数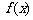 和
和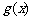 对其定义域上的任意实数
对其定义域上的任意实数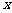 分别满足:
分别满足: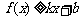 和
和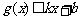 ,则称直线
,则称直线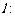
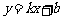 为
为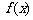 和
和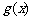 的“隔离直线”.已知
的“隔离直线”.已知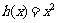 ,
,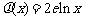 (其中
(其中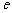 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求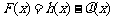 的极值;
的极值;
(Ⅱ) 函数 和
和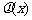 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
 . 在
. 在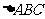 中,角A、B、C所对的
边分别为
中,角A、B、C所对的
边分别为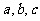 ,且
,且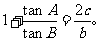
(Ⅰ)求角A;(Ⅱ)若向量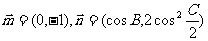 ,试求
,试求 的最小值。
的最小值。
16.如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离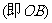 为2m,在圆环上设置三个等分点A1,A2,A3。点C为
为2m,在圆环上设置三个等分点A1,A2,A3。点C为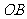 上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为ym。
上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为ym。
(1)设∠CA1O =  (rad),将y表示成θ的函数关系式;
(rad),将y表示成θ的函数关系式;
(2)请你设计 ,当角θ正弦值的大小是多少时,细绳总长y最小,并指明此时 BC应为多长。
,当角θ正弦值的大小是多少时,细绳总长y最小,并指明此时 BC应为多长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com