
22. (本小题满分14分)
已知函数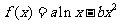 图象上一点
图象上一点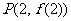 处的切线方程为
处的切线方程为 .
.
(Ⅰ)求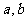 的值;
的值;
(Ⅱ)若方程 在
在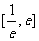 内有两个不等实根,求
内有两个不等实根,求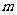 的取值范围(其中
的取值范围(其中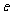 为自然对数的底数);
为自然对数的底数);
(Ⅲ)令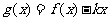 ,若
,若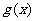 的图象与
的图象与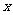 轴交于
轴交于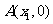 ,
,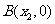 (其中
(其中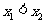 ),
),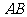 的中点为
的中点为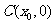 ,求证:
,求证: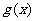 在
在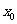 处的导数
处的导数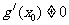 .
.
21. (本小题满分12分)
已知数列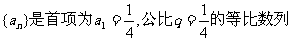 ,设
,设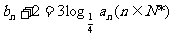 ,数列
,数列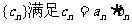 。
。
(1)求证: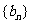 是等差数列;
是等差数列;
(2)求数列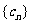 的前n项和Sn;
的前n项和Sn;
(3)若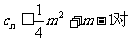 一切正整数n恒成立,求实数m的取值范围。
一切正整数n恒成立,求实数m的取值范围。
20.(本小题满分12分)
某商店经销一种奥运纪念品,每件产品成本为30元,且每卖出一件产品,需向税务部门上交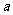 元(
元(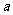 为常数,
为常数,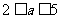 )的税收,设每件产品的日售价为
)的税收,设每件产品的日售价为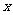 元(
元(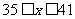 ),根据市场调查,日销售量与
),根据市场调查,日销售量与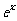 (
(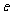 为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。
为自然对数的底数)成反比,已知每件产品的日售价为40元,日销售量为10件。
(1)求商店的日利润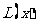 元与每件产品的日售价
元与每件产品的日售价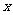 元的函数关系式;
元的函数关系式;
(2)当每件产品的日售价为多少元时该商店的日利润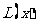 最大,说明理由。
最大,说明理由。
17. (本小题满分12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且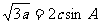
(Ⅰ)确定角C的大小:
(Ⅱ)若c=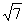 ,且△ABC的面积为
,且△ABC的面积为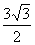
 ,求a+b的值。
,求a+b的值。
18.(本小题满分12分)
已知全集U = R,非空集合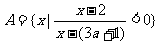 ,
,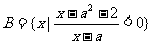 .
.
(Ⅰ)当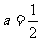 时,求(∁U
时,求(∁U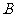 )
)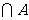 ;
;
(Ⅱ)命题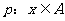 ,命题
,命题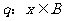 ,若
,若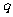 是
是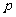 的必要条件,求实数
的必要条件,求实数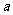 的取值范围.
的取值范围.
19(本题满分12分)
如图,已知四棱锥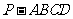 的底面是正方形,
的底面是正方形,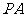 ⊥底面
⊥底面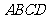 ,且
,且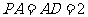 ,点
,点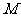 、
、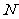 分别在侧棱
分别在侧棱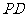 、
、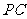 上,且
上,且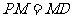
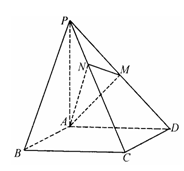 (Ⅰ)求证:
(Ⅰ)求证: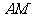 ⊥平面
⊥平面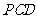 ;
;
(Ⅱ)若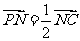 ,求平面
,求平面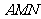 与平面
与平面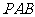 的所成锐二面角的大小
的所成锐二面角的大小
16.已知定义在R上的函数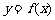 满足条件
满足条件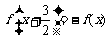 ,且函数
,且函数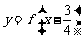 是奇函数,给出以下四个命题:
是奇函数,给出以下四个命题:
①函数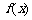 是周期函数;②函数
是周期函数;②函数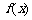 的图象关于点
的图象关于点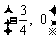 对称;
对称;
③函数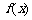 是偶函数;④函数
是偶函数;④函数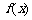 在R上是单调函数.
在R上是单调函数.
在上述四个命题中,正确命题的序号是__________(写出所有正确命题的序号)。
15.若实数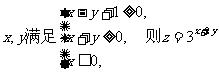 的值域是
;
的值域是
;
14. 已知四棱锥P-ABCD的三视图如图所示,则该四棱锥的表面积为 ;
已知四棱锥P-ABCD的三视图如图所示,则该四棱锥的表面积为 ;
13.已知函数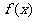 =
=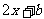 ,
,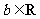 ,若
,若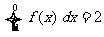 ,则
,则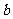 =
;
=
;
12.在Rt△ABC中,∠C = 90°,那么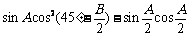 ( )
( )
A.有最大值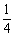 和最小值为0 B.有最大值
和最小值为0 B.有最大值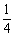 ,但无最小值
,但无最小值
C.既无最大值,也无最小值 D.有最大值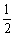 ,但无最小值
,但无最小值
Ⅱ卷(非选择题,共90分)
11.设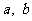 是正实数,以下不等式:
是正实数,以下不等式:
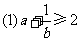 ;
; ;
; 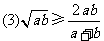 ;
;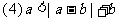 ,
,
其中恒成立的有
A.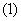
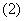 B.
B.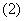
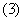 C.
C.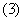
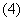 D.
D.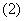
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com