
3.(12分)某制造商3月生主了一批乒乓球,随机抽样100个进行检查,测得每个球的直径(单位mm),将数据分组如下:
|
分组 |
频数 |
频率 |
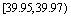 |
10 |
|
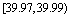 |
20 |
|
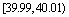 |
50 |
|
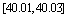 |
20 |
|
|
合计 |
100 |
|
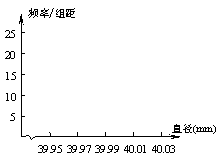
⑴请将上表中补充完成频率分布直方图(结果保留两位小数),并在上图中画出频率分布直方图;
⑵若以上述频率作为概率,已知标准乒乓球的直径为40.00mm,试求这批球的直径误差不超过0.03mm的概率;
⑶统计方法中,同一组数据经常用该组区间的中点值(例如区间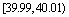 的中点值是40.00)作为代表.据此,估计这批乒乓球直径的平均值(结果保留两位小数).
的中点值是40.00)作为代表.据此,估计这批乒乓球直径的平均值(结果保留两位小数).
2.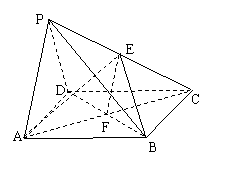 如图,四棱锥P-ABCD的底面是边长为2的正方形,侧面PAD是等腰直角三角形,PA=PD,又平面PAD
如图,四棱锥P-ABCD的底面是边长为2的正方形,侧面PAD是等腰直角三角形,PA=PD,又平面PAD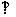 平面ABCD,
平面ABCD,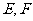 分别为
分别为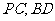 的中点。
的中点。
(1)求侧视图的面积;
(2)求证:平面PDC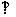 平面PAD;
平面PAD;
(3)求三棱锥E-AFB的体积。
1.(本小题满分14分) 已知函数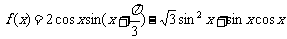
(1)求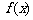 的最小正周期;(2)求
的最小正周期;(2)求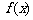 的单调增区间;(3)当
的单调增区间;(3)当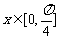 时,求
时,求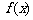 的值域。
的值域。
3.(本小题满分12分)
某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h),可以把这批电子元件分成第一组[100,200],第二组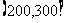 ,第三组
,第三组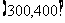 ,第四组
,第四组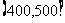 ,第五组
,第五组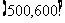 ,第六组
,第六组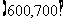 ,由于工作不慎将部分数据丢失,现有以下部分图表:
,由于工作不慎将部分数据丢失,现有以下部分图表:

|
分组 |
[100,200] |
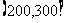 |
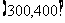 |
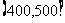 |
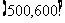 |
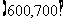 |
|
频数 |
B |
30 |
E |
F |
20 |
H |
|
频率 |
C |
D |
0.2 |
0.4 |
G |
I |
(I)求图2中的A及表格中的B,C,D,E,F,G,H,I的值;
(II)求上图中阴影部分的面积;
(III)若电子元件的使用时间超过300h,则为合格产品,求这批电子元件合格的概率。
2.已知向量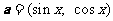 ,
,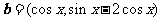 ,
,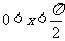 .
.
(Ⅰ)若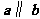 ,求
,求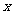 ; (Ⅱ)设
; (Ⅱ)设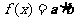 ,
,
(1)
求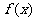 的单调增区间;
的单调增区间;
(2)
函数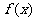 经过怎样的平移才能使所得的图象对应的函数成为奇函数?
经过怎样的平移才能使所得的图象对应的函数成为奇函数?
1. (本小题满分14分)
(本小题满分14分)
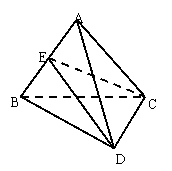
如图,已知空间四边形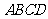 中,
中,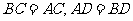 ,
,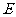 是
是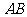 的中点.
的中点.
求证:
(1)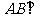 平面CDE;
平面CDE;
 (2)平面
(2)平面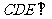 平面
平面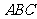 .
.
(3)若G为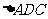 的重心,试在线段AE上确定一点F,使得GF//平面CDE.
的重心,试在线段AE上确定一点F,使得GF//平面CDE.
3.(本题满分12分)
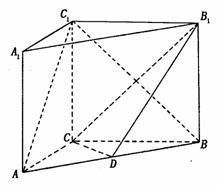 如图, 在直三棱柱ABC-A1B1C1中,AC=3,
如图, 在直三棱柱ABC-A1B1C1中,AC=3,
BC=4,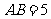 ,AA1=4,点D是AB的中点,
,AA1=4,点D是AB的中点,
(1)求证:AC⊥BC1;
(2)求证:AC 1//平面CDB1;
(3)求三棱锥C1-B1CD的体积
2.(本题满分12分)口袋中有质地、大小完全相同的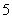 个球,编号分别为
个球,编号分别为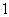 、
、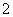 、
、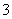 、
、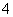 、
、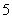 ,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢。
,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢。
(1)求两个编号的和为6的概率;
(2)求甲赢的事件发生的概率。
1.(本题满分12分)已知函数f(x)=cos2x+sinxcosx(x∈R).
(I)求f(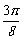 )的值;
(Ⅱ)求f(x)的单调递增区间.
)的值;
(Ⅱ)求f(x)的单调递增区间.
3、(本小题满分12分)
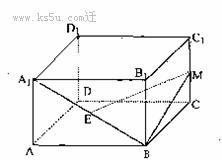 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=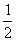 AB=2,点E、M分别为A1B、C1C的中点。
AB=2,点E、M分别为A1B、C1C的中点。
(Ⅰ)求证:EM∥平面A1B1C1D1;
(Ⅱ)求几何体B-CME的体积;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com