
2.汽车A由静止开始向东运动,加速度为a,汽车B同时以速度v向西做匀速运动,汽车A中乘客看到的汽车B的运动是
A.向西的初速度大小为v的匀加速直线运动
B.向西的初速度大小为v的匀减速直线运动
C.向东的初速度为零的匀加速直线运动
D.向西的初速度为零的匀加速直线运动
1.甲、乙、丙三辆汽车同时以相同的速度经过某一路标,此后甲一直做匀速直线运动,乙先加速后减速,丙先减速后加速,它们经过下一个路标时的速度仍相同,则
A.甲车先经过下一个路标 B.乙车先经过下一个路标
C.丙车先经过下一个路标 D.无法判断谁先经过下一个路标
22.(本小题满分12分)
数列{an}的前n项和为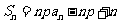 (
(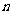 ∈N*
,
∈N*
,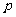 为常数),且
为常数),且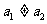 .
.
(Ⅰ)求p的值;
(Ⅱ) 求证:数列{an}是等差数列;
(III)将数列{an}的前n项随机打乱顺序得到数列{bn}的前n项,
试比较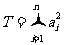 和
和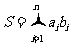 的大小.
的大小.
21.(本小题满分12分)
已知椭圆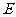 :
: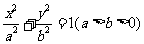 的右焦点为
的右焦点为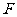 , 过原点和
, 过原点和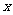 轴不重合的直线与椭圆
轴不重合的直线与椭圆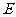 相交于
相交于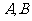 两点.
两点.  ,
,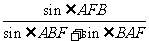 的最小值为
的最小值为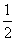 .
.
(Ⅰ)求椭圆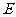 的方程;
的方程;
(Ⅱ) 若直线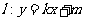 与椭圆
与椭圆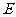 交于
交于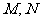 ,以线段
,以线段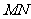 为直径的圆过
为直径的圆过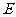 的右顶点,求证直线
的右顶点,求证直线 过定点.
过定点.
20.(本小题满分12分)
函数 .
.
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ) 求证:当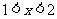 时,不等式
时,不等式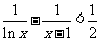 恒成立.
恒成立.
19.(本小题满分12分)
如图,在三棱锥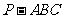 中,已知
中,已知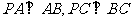 ,
,
 ,
,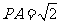 ,
,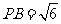 ,
,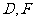 分别是
分别是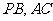 的中点.
的中点.
(Ⅰ)求证:直线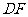 ⊥平面
⊥平面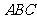 ;
;
(Ⅱ)求二面角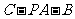 的大小.
的大小.
18.(本小题满分12分)
某公司客服中心有四部咨询电话,某一时刻每部电话能否被接通是相互独立的.已知每部电话响第一声时被接通的概率是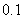 ,响第二声时被接通的概率是
,响第二声时被接通的概率是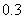 ,响第三声时被接通的概率是
,响第三声时被接通的概率是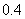 ,响第四声时被接通的概率是
,响第四声时被接通的概率是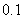 .假设有
.假设有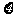 部电话在响四声内能被接通.
部电话在响四声内能被接通.
(Ⅰ)求四部电话至少有一部在响四声内能被接通的概率;
(Ⅱ) 求随机变量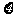 的分布列及期望.
的分布列及期望.
17.(本小题满分12分)
已知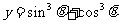 ,
, 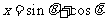 ,
,
(Ⅰ)把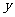 表示为
表示为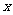 的函数
的函数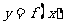 并写出定义域;
并写出定义域;
(Ⅱ)求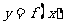 的最值.
的最值.
16.依次写出数 ,
,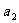 ,
, ,…,
,…,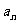 ,…,法则如下:如果
,…,法则如下:如果 为自然数且未写出过,则写
为自然数且未写出过,则写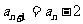 ,否则就写
,否则就写 ,那么
,那么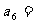 .
.
15.若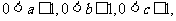 则
则 的最大值为__________.
的最大值为__________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com