
7、解:1)设 ,则
,则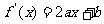
由已知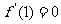 ∴
∴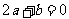
又抛物线过点(0,-3),∴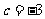
又 ,∴
,∴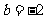
∴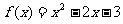
2)由1)可知: ∴
∴
∴由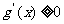 得:
得: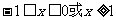
∴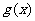 的递增区间为:
的递增区间为: 。
。
例1、解:
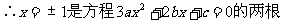

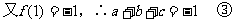


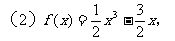

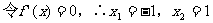
列表:
|
x |
(-∞,-1) |
-1 |
(-1,1) |
1 |
(1,+∞) |
|
y/ |
+ |
0 |
- |
0 |
+ |
|
y |
↗ |
极大 |
↘ |
极小 |
↗ |
由表可知,x=-1,f(x)有极大值
x=1时,f(x)有极小值
例2、1)∵ ,∴要使
,∴要使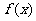 在(0,1)上单调递增,则有:
在(0,1)上单调递增,则有:
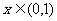 时,
时, 恒成立。
恒成立。
∴ ,即当
,即当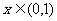 时,
时,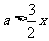 恒成立,∴
恒成立,∴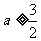
即: 的取值范围是
的取值范围是 。
。
2)由 ,令
,令 ,得
,得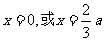 ,
,
∵ ∴当
∴当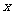 变化时,
变化时,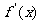 的取值符号易判断,根据单调性,有:
的取值符号易判断,根据单调性,有:
 ;
;
∴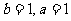
3)当 时,
时,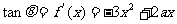
由 ,得
,得
即 时,
时,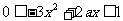 恒成立。
恒成立。
当 时,
时,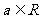 ,
,
当 时,由
时,由 恒成立,
恒成立, 恒成立,
恒成立,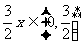
∴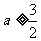 ;
;
又由 恒成立,
恒成立, 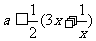
∴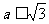 (等号在
(等号在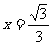 时取得)
时取得)
综上, 。
。
例3、解: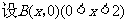
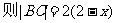
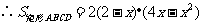
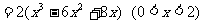
∴
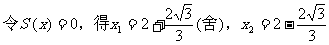
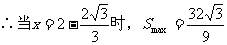
(该问题有最大值,且有一个极值点,所以x2即为最大值点)
冲刺强化训练(7)
1、D; 2、4; 3、D; 4、5; 5、13,4; 6、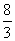 ;
;
9.
已知曲线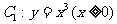 与曲线
与曲线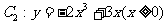 交于点
交于点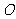 、
、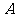 ,直线
,直线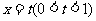 与曲线
与曲线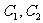 、分别相交于点B、D.
、分别相交于点B、D.
(1)
写出四边形ABOD的面积S与t的函数关系式 ;
;
(2)
讨论 的单调性,并求出
的单调性,并求出 的最大值。
的最大值。
第7讲 导数的应用
8. 设函数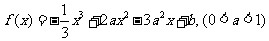
(1) 求函数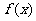 的单调区间、极值;
的单调区间、极值;
(2) 若当 时,恒有
时,恒有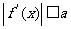 ,试确定
,试确定 的取值范围。
的取值范围。
7.
已知二次函数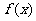 满足:①在
满足:①在 时有极值;②图象过点(0,-3)且在该点处的切线与直线
时有极值;②图象过点(0,-3)且在该点处的切线与直线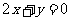 平行。
平行。
1) 求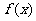 的解析式;
的解析式;
2) 求函数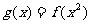 的单调递增区间。
的单调递增区间。
6.
曲线 在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为_________.
在点(1,1)处的切线与x轴、直线x=2所围成的三角形的面积为_________.
5. 函数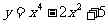 在区间[-2,2]上的最大值为______,最小值为_______。
在区间[-2,2]上的最大值为______,最小值为_______。
4. 函数 ,已知
,已知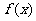 在
在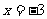 时取得极值,则
时取得极值,则 。
。
3. 函数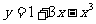 有( )
有( )
A.极小值-1,极大值1 B. 极小值-2,极大值3
C.极小值-2,极大值2 D. 极小值-1,极大值3
2. 已知函数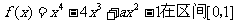 上单调递增,在区间[1,2]上单调递减,则实数a=_____________
上单调递增,在区间[1,2]上单调递减,则实数a=_____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com