
25.(本题满分10分)已知二项式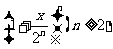 .
.
(1)当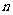 =3时,写出这个二项式的展开式;
=3时,写出这个二项式的展开式;
(2)若对任意的正整数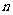
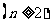 ,展开式的第二项恒大于第三项,求
,展开式的第二项恒大于第三项,求 的取值范围.
的取值范围.


|
数学(理)答题卷 2010.01
24.(本题满分9分)一袋中装有大小相同的2个白球和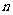 个红球
个红球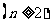 ,每次从中摸出2个球(每次摸球后把2个球放回袋中),若摸出的2个球颜色相同为中奖,否则为不中奖.
,每次从中摸出2个球(每次摸球后把2个球放回袋中),若摸出的2个球颜色相同为中奖,否则为不中奖.
(1)若一次摸球中奖的概率为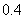 ,求
,求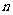 的值;
的值;
(2)设摸球2次,至少有一次中奖的概率为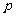 ,求
,求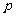 的最小值及此时
的最小值及此时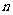 的值.
的值.
23.(本题满分8分)某人进行一项试验,若试验成功,则停止试验,否则重新试验一次.若试验3次均失败,则放弃试验.已知此人每次试验成功的概率均为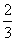 ,设随机变量X表示此人试验的次数.
,设随机变量X表示此人试验的次数.
(1)求X的分布列;
(2)求X的数学期望.
22.(本题满分7分)有4张分别标有数字1,2,3,4的红色卡片和2张分别标有数字1,2的蓝色卡片,从这6张卡片中取出不同的4张卡片.
(1)如果要求至少有1张蓝色卡片,那么有多少种不同的取法?
(2)如果取出的4张卡片所标数字之和等于10,并将它们排成一行,那么有多少种不同的排法?
21.(本题满分6分)从某项综合能力测试中抽取100人的成绩,统计如下表:
|
分数 |
5 |
4 |
3 |
2 |
1 |
|
人数 |
20 |
10 |
30 |
30 |
10 |
(1)根据上面统计结果,求分数不小于3分的频率;
(2)求这100人成绩的平均分与标准差.
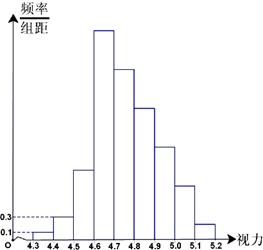
20.为了研究某高校大学新生的视力情况,
随机地抽查了该校100名新生的视力
情况,得到频率分布直方图如右图所
示.已知前4组的频数从左到右依次
成等比,后6组的频数从左到右依次
成等差.若规定视力低于5.0的学生
属于近视学生,试估计该校新生的近
视率 的大小为 ▲ .
的大小为 ▲ .
19.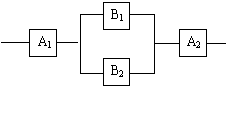 一个元件能正常工作的概率叫做这个元件的可靠
一个元件能正常工作的概率叫做这个元件的可靠
性,设构成系统的每个元件的可靠性均为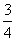 ,且
,且
各个元件能否正常工作是相互独立的,则如右图
 由4个元件构成系统的可靠性为 ▲ .
由4个元件构成系统的可靠性为 ▲ .
18.把一颗骰子抛掷2次,观察出现的点数,并记第一次出现的点数为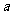 ,第二次出现的点数为
,第二次出现的点数为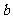 .若事件“点
.若事件“点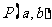 落在直线
落在直线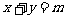 (
(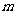 为常数)上”的概率最大,则
为常数)上”的概率最大,则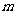 = ▲ .
= ▲ .
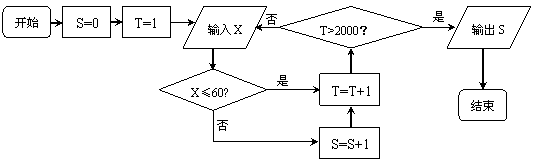
17. 我市某机构调查小学生课业负担的情况,设平均每人每天做作业时间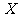 (单位:分钟),按时间分下列四种情况统计:①0-30分钟;(注:0-30表示(0,30].下同)②30-60分钟;③60-90分钟;④90分钟以上,有2000名小学生参加了此项调查,下图是此次调查中某一项的流程图,其输出的结果是1500,则平均每天做作业时间在0-60分钟内的学生的频率是 ▲
.
(单位:分钟),按时间分下列四种情况统计:①0-30分钟;(注:0-30表示(0,30].下同)②30-60分钟;③60-90分钟;④90分钟以上,有2000名小学生参加了此项调查,下图是此次调查中某一项的流程图,其输出的结果是1500,则平均每天做作业时间在0-60分钟内的学生的频率是 ▲
.
16.完成进位制之间的转化: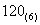 = ▲
= ▲ 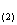 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com