
 读“世界局部地区图”,当图中PQ线为昏线且与极圈相切时,回答1-2题。
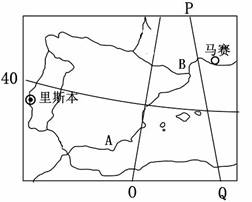
读“世界局部地区图”,当图中PQ线为昏线且与极圈相切时,回答1-2题。
1.此时,里斯本与马赛相比
A.正午太阳高度小 B.白昼时间长
C.自转线速度小 D.自转角速度大
2.A、B两地均盛产葡萄。两地相比,A地的优势是
A.交通便捷 B.市场广阔 C.鲜果上市早 D.技术条件好
23.(本题满分18分,第(1)小题6分,第(2)小题6分,第(3)小题6分)
若数列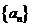 满足:
满足: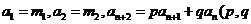 是常数),则称数列
是常数),则称数列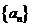 为二阶线性递推数列,且定义方程
为二阶线性递推数列,且定义方程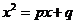 为数列
为数列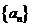 的特征方程,方程的根称为特征根; 数列
的特征方程,方程的根称为特征根; 数列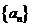 的通项公式
的通项公式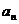 均可用特征根求得:
均可用特征根求得:
①若方程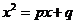 有两相异实根
有两相异实根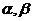 ,则数列通项可以写成
,则数列通项可以写成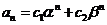 ,(其中
,(其中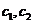 是待定常数);
是待定常数);
②若方程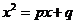 有两相同实根
有两相同实根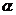 ,则数列通项可以写成
,则数列通项可以写成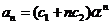 ,(其中
,(其中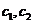 是待定常数);
是待定常数);
再利用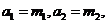 可求得
可求得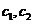 ,进而求得
,进而求得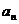 .
.
根据上述结论求下列问题:
(1)当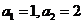 ,
,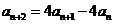 (
(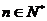 )时,求数列
)时,求数列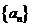 的通项公式;
的通项公式;
(2)当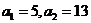 ,
,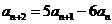 (
(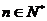 )时,若数列
)时,若数列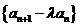 为等比数列,求实数
为等比数列,求实数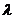 的值;
的值;
(3)当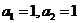 ,
,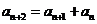 (
(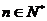 )时,求
)时,求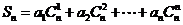 的值.
的值.
22.(本题满分16分,第(1)小题8分,第(2)小题8分,)
己知双曲线的中心在原点,右顶点为
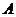 (1,0),点
(1,0),点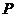 、Q在双曲线的右支上,点
、Q在双曲线的右支上,点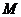 (
(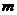 ,0)到直线
,0)到直线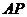 的距离为1.
的距离为1.
(1)若直线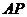 的斜率为
的斜率为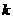 且有
且有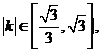 求实数
求实数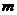 的取值范围;
的取值范围;
(2)当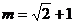 时,
时,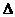
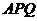 的内心恰好是点
的内心恰好是点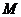 ,求此双曲线的方程.
,求此双曲线的方程.
21.(本题满分16分,第(1)小题6分,第(2)小题10分)
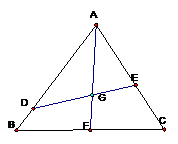 如图,已知点
如图,已知点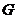 是边长为
是边长为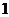 的正三角形
的正三角形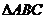 的中心,线段
的中心,线段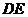 经过点
经过点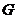 ,并 绕点
,并 绕点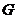 转动,分别交边
转动,分别交边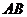 、
、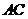 于点
于点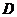 、
、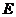 ;设
;设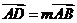 ,
,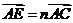 , 其中
, 其中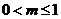 ,
,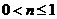 。
。
(1)求证: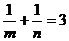 ;
;
(2)求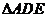 面积的最大和最小值,并指出相应的
面积的最大和最小值,并指出相应的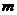 、
、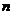 的值.
的值.
20.(本题满分14分,第(1)小题6分,第(2)小题8分)
设全集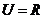 ,关于
,关于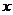 不等式
不等式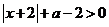 (
(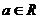 )的解集为
)的解集为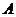 .
.
(1)分别求出当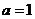 和
和 时的集合
时的集合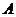 ;
;
(2)设集合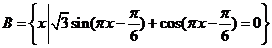 ,若
,若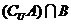 中有且只有三个元素,求实数
中有且只有三个元素,求实数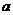 的取值范围.
的取值范围.
19.(本题满分12分,第(1)小题6分,第(2)小题6分)
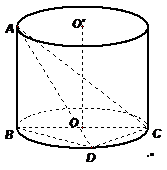 如图,
如图,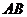 是圆柱体
是圆柱体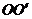 的一条母线,
的一条母线,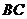 过底面圆的圆心
过底面圆的圆心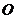 ,
,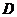 是圆
是圆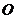 上不与点
上不与点 、
、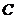 重合的任意一点,已知棱
重合的任意一点,已知棱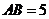 ,
,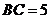 ,
, 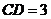 .
.
(1)求直线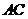 与平面
与平面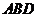 所成的角的大小;
所成的角的大小;
(2)将四面体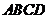 绕母线
绕母线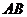 转动一周,求
转动一周,求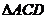 的三边在旋转
过程中所围成的几何体的体积.
的三边在旋转
过程中所围成的几何体的体积.
18.给定正数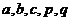 ,其中
,其中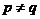 ,若
,若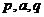 成等比数列,
成等比数列,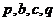 成等差数列,则关于
成等差数列,则关于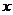 的一元二次方程
的一元二次方程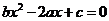 ( ).
( ).
(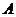 ) 有两个相等实根
(
) 有两个相等实根
( ) 有两个相异实根
) 有两个相异实根
(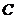 ) 有一个实根和一个虚根
(
) 有一个实根和一个虚根
(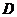 ) 有两个共轭虚根
) 有两个共轭虚根
17.函数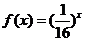 与其反函数的图象的交点个数为( ).
与其反函数的图象的交点个数为( ).
( )
)  个
(
个
( ) 3个 (
) 3个 ( ) 5个 (
) 5个 ( ) 无法确定
) 无法确定
16.长度分别为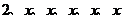 的六条线段能成为同一个四面体的六条棱的充要条件是( ).
的六条线段能成为同一个四面体的六条棱的充要条件是( ).
(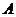 )
) 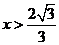 (
( )
) 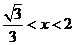 (
(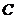 )
) 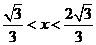 (
(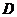 )
) 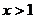
15.方程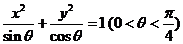 所表示的曲线是( ).
所表示的曲线是( ).
(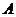 ) 双曲线 (
) 双曲线 ( ) 焦点在
) 焦点在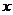 轴上的椭圆
轴上的椭圆
(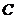 ) 焦点在
) 焦点在 轴上的椭圆
(
轴上的椭圆
( ) 以上答案都不正确
) 以上答案都不正确
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com