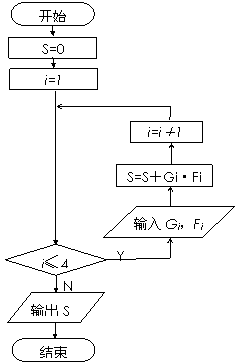
3. 设计一个计算的算法．图中给出了程序

2. 若复数是纯虚数，则实数的值为

　　 A．1　　　　 B. 或1　 　　C. 　　　D. 或3

1. 某学校有教师人，其中高级教师人，中级教师人，初级教师人. 现按职称分层抽样选出名教师参加教工代表大会，则选出的高、中、初级教师的人数分别为

A．　 　　　B．　 　　　C．　 　　　　　D．

21．(本小题满分14分)

已知数列满足：．

(1)求数列的通项公式及前项和；

(2)令，,

求证：．

20．(本小题满分14分)

设函数,二次函数，其中常数．

(1)若函数与在区间内均为增函数，求实数的取值范围；

(2)当函数与的图象只有一个公共点且存在最大值时，记的最大值为，求函数的解析式．

19．(本小题满分14分)

如图，在直角梯形中，，点在线段的延长线上.曲线段上任一点到、两点的距离之和都相等．

(1)建立适当的直角坐标系，求曲线段的方程；

(2)试问：过点能否作一条直线与曲线段相交于两点、，使得线段以C为中点？若能，则求直线的方程；若不能，则说明理由．

18．(本小题满分14分)

如图，在四棱锥中，平面，，且平分，为的中点， ,,.　　　　　

(1)求证：∥平面；

(2)求证:平面；

(3)求四棱锥的体积.

17．(本小题满分12分)

为了让学生更多的了解“数学史”知识，某中学高二年级举办了一次“追寻先哲的足迹，倾听数学的声音”的数学史知识竞赛活动，共有名学生参加了这次竞赛．为了解本次竞赛的成绩情况，从中抽取了部分学生的成绩(得分均为整数，满分为分)进行统计．请你根据频率分布表，解答下列问题：

序号 ()	分组 (分数)	组中值	频数 (人数)	频率
			①
				②
			③	④
合　　 计

(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案)；

(2)为鼓励更多的学生了解“数学史”知识，成绩不低于80分的同学能获奖，请估计在参加的800名学生中大概有多少同学获奖？

　 (3)在上述统计数据的分析中有一项计算见算法流程图，求输出的值．

16.(本小题满分12分)

已知向量，其中＞0，且，又函数的图象两相邻对称轴之间的距离为.

(1)求的值；

(2) 求函数在区间上的最大值与最小值及相应的值．

(一)必做题(11-13题．)

11. 已知曲线在处的切线与曲线在处的切线互相平行，则的值为　　　　　　　　 ． 　

12. 年北京国庆阅兵式上举行升旗仪式．

如图，在坡度为的观礼台上，某一列座位

与旗杆在同一个垂直于地面的平面上，在该列

的第一排和最后一排测得旗杆顶端的仰角分别

为和，且第一排和最后一排的距离为　　　　　第12题图

米，则旗杆的高度为　　 米 .

13. 若定义在R上的偶函数在区间上是减函数，且，则不等式的解集为______.　

(二)选做题(14、15题，考生只能从中选做一题,两题都选的只计算第14题的得分．)

14. 如图，在中，∥，∥，

︰＝︰，，则＝____.

　　　 第14题图

15. 若为曲线()的弦的中点，则该弦所在直线的普通方程为_____________．