
7.某位高三学生要参加高校自主招生考试,现从6所高校中选择3所报考,其中两所学校的
考试时间相同.则该学生不同的报名方法种数是
A. 12 B. 15 C. 16 D. 20
6.若称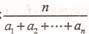 为n个正数,则
为n个正数,则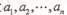 的“均倒数”,数列
的“均倒数”,数列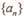 的各项均为正,且
的各项均为正,且
其前n项的“均倒数”为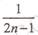 ,则数列
,则数列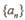 的通项公式为
的通项公式为
A.2n-1 B. 4n-3 C. 4n -1 D.4n-5
5.己知直线线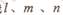 ,平面
,平面 ,有以下命题:
,有以下命题:
①.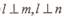 且
且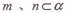 ,则
,则
②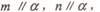 且
且
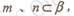 则
则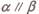
③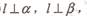 则
则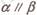
④若平面a内不共线的三点到平面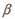 的距离相等,则
的距离相等,则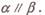
则正确命题有
A.O个 B.1个 C.2个 D.3个
4.已知双曲线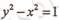 的离心率为e,则抛物线
的离心率为e,则抛物线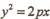 的焦点为
的焦点为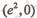 ,则p的值为
,则p的值为
A .-2 B.-4 C.2 D.4
3.若向量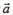 与向量
与向量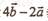 垂直,其中向量
垂直,其中向量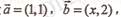 ,则实数x的值为
,则实数x的值为
A.-2 B.-1 C.1 D. 2
合题目要求的.
1.已知集合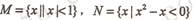 ,
,
A.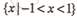 B.
B. 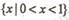 c.
c. 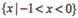 D.
D. 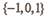
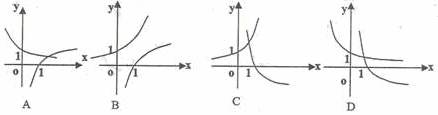
2-当O<a<l时,在同一坐标系中,函数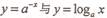 的图象是
的图象是
24. (本小题满分10分)选修4-5:不等式选讲
已知函数 .
.
(Ⅰ)解不等式 ≤4;
≤4;
(Ⅱ)若存在x使得 ≤0成立,求实数a的取值范围.
≤0成立,求实数a的取值范围.
吉林市普通中学2009-2010学年度高中毕业班下学期期中教学质量检测
23.(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系中,以原点O为极点,x 轴为正半轴为极轴,建立极坐标系.
设曲线 (
( 为参数);
直线
为参数);
直线 .
.
(Ⅰ)写出曲线 的普通方程和直线l的直角坐标方程;
的普通方程和直线l的直角坐标方程;
(Ⅱ)求曲线 上的点到直线l的最大距离.
上的点到直线l的最大距离.
22.(本小题满分10分)
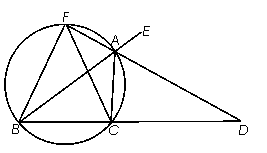 如图,已知AD是△ABC的外角ÐEAC的平分线,交BC的延长线于点D,延长DA 交△ABC的外接圆于点F,连结FB、FC.
如图,已知AD是△ABC的外角ÐEAC的平分线,交BC的延长线于点D,延长DA 交△ABC的外接圆于点F,连结FB、FC.
(Ⅰ)求证:FB=FC;
(Ⅱ)求证:FB2=FA·FD;
(Ⅲ)若AB是△ABC外接圆的直径,
ÐEAC=120°,BC=6cm,求AD的长.
|
21.(本小题满分12分)
已知椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,且倾斜角为60
,且倾斜角为60 的直线l过点
的直线l过点
 和椭圆C的右焦点F.
和椭圆C的右焦点F.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若已知D(3,0),点M,N是椭圆C上不重合的两点,且 ,求实数
,求实数 的取值范围.
的取值范围.
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com