19.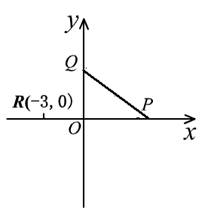(本题满分14分)

(1)　　　 解：设，由，

得　 ，　 ……………………3分

由得，

即，　　 　……………………………6分

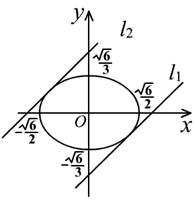故点M的轨迹C的方程为.　　 　………………7分

(2)由得，…9分

得 　…………………………………13分

所以的取值范围为　 　　……………14分

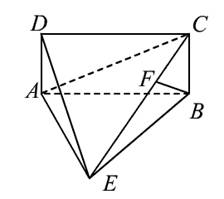
18．(本题满分14分)

(1)证明：

ABCD是矩形

BCAB

平面EAB平面ABCD，平面EAB平面ABCD=AB，BC平面ABCD

BC平面EAB

EA平面EAB

BCEA　　　　　　 　　………………………2分

BF平面ACE，EA平面ACE

　BF EA　　　　　　 　　………………………4分

　BC BF=B，BC平面EBC，BF平面EBC

　EA平面EBC　　　　　 ………………… ……6分

BE平面EBC

　EA BE　　　　　　　　 ………………………7分

(2) 解： EA BE

AB=　　　　　　

　　 　……………………9分

设O为AB的中点，连结EO，

AE=EB=2

EOAB

平面EAB平面ABCD

EO平面ABCD，即EO为三棱锥E-ADC的高，且EO=　 ……………12分

　　 ……………………14分

17. (本题满分12分)

解：(1) 依题知得　 　即　 　　……3分

　也就是 ，又，所以　　 ………………………6分

(2) ，且，所以 　　……………8分

又

得.　 　　　　　　　　　　　　　　　　　　………………………12分

16.(本题满分12分)

解：(1)在全体样本中随机抽取1个，抽到B组疫苗有效的概率约为其频率 …… (1分)

即 　　　　　　　　　　　　　　　　　　………………(4分)

(2)C组样本个数为y+z＝2000－(673+77+660+90)＝500，　 …………………(5分)

　现用分层抽样的方法在全体样本中抽取360个测试结果，问应在C组抽取个数为

　个　　　　　　　　　　　　　　　　　　　　 　　…………………(8分)

(3)设测试不能通过事件为A ，C组疫苗有效与无效的可能的情况记为(y，z)……(9分)

　由(2)知 　，且　 ,基本事件空间包含的基本事件有：

(465，35)、(466，34)、(467，33)、……(475，25)共11个　　　 ……………… (10分)

　若测试不能通过，则77+90+z>200，即z>33

事件A包含的基本事件有：((465，35)、(466，34)共2个

　　　　　　　　　　　　　　　　　　　　　　　 　…………………(11分)

故不能通过测试的概率为　　　　 　　　　　　　　　　　　　　　　…………(12分)

13． 解析：，故解得

11． 解析：两条直线的交点为(-3，-1)，所以与直线平行的直线为，即．

(二)(选做题) 　14.　 相切；　　　 15.　

简答或提示：

1． 解析：∵∴={0},选D.

2． 解析: ,选A.

5． 解析:画出可行域,可知过点(1,1)取最小值.其值为3， 选C.

6. 　解析：由，，故选C.

7． 解析：由抛物线定义可得圆C半径为2，选B．

8． 解析： ①和④是真命题，选B．

9． 解析：由平均数计算公式检验可得到x=2，选A.

10．解析：依题意知的图象关于直线对称，设方程 的3个不同的实数解是从小到大排列，则_，故_，所以

_，故选D.

(一)(必做题)　 11．　 　；　　 12.　 420；　　 13.　 1；

21．(本题满分14分)已知，其中是无理数，且， .

(1)若时, 求的单调区间、极值；

(2)求证：在(1)的条件下，；

(3)是否存在实数，使的最小值是，若存在，求出的值；若不存在，说明理由.

数学(文科)评分标准

20．(本题满分14分)设数列的前n项和为，点恒在函数的图象上；数列为等差数列，且.

(1)求数列的通项公式；

(2)若　 ，为数列的前n项和，求证：