21．证明：(1)∵底面，

∴，又∵底面是正方形，

∴，∵，

∴平面，

又∵平面

∴平面平面．

解：(2)连接，由(1)知平面，

∴在平面内的射影是，

∴就是与平面所成的角，

又∵，

∴在中，，

而在正方形中，，

∴在中，有，

从而，即与平面所成的角为．

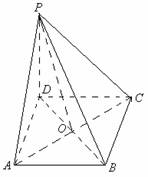
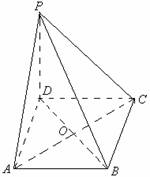
21．如图所示，四棱锥的底面为正方形，底面，．

(1)求证：平面平面；

(2)求与平面所成的角的大小．

20．解：设“甲获胜”为事件，“乙获胜”为事件，

　　　　 (1)甲、乙两人都获胜的概率为

　　　　　　 ；

　　　　 (2)甲、乙两人中恰有一人获胜的概率为

　　　　 　　　　　　　　　　　．

20．(本小题满分8分，其中(1)和(2)各4分)

　 甲、乙两人分别与丙进行乒乓球比赛，甲获胜的概率为，乙获胜的概率为，计算：

　 (1)甲、乙两人都获胜的概率；

　 (2)甲、乙两人中恰有一人获胜的概率．

19．解：(1)∵，

　　　　　 　∴，

　　　 　　又

　　 　　　　∴，

　　　　　 　　(，

　　　 　　解之得或(不合题意舍去)

　　　 　　又，∴；

(2)由余弦定理知，

∴，

又，

∴ ，

解方程组，

得或．

19．(本小题满10分，其中(1)和(2)各5分)

在中、、分别是角、、所对的边，且．

(1)求角C的大小；

(2)若，求、的值．

18．解：(1)∵，

　　　　　　 ∴，

　　　　　　 由于直线与的图像相切于点，

　　　　　　 ∴，　　　 ①

　　　　　　 且方程有两个相等的实根，

　　　　　　 ∴，

　　　　　　 　即，　　　 　②

　　　　　 　　联立①②解得：，

　　　　　 ∴；

　　　　 (2)∵为数列的前项和，

　　　　　　 ∴，

　　　　　 　∴当时，，

　　　　　　　 当时，，

　　　　　　 ．

18．(本小题满分14分，其中(1)8分，(2)6分)

已知函数满足，且直线与的图象相切

于点，(1)求函数的解析式；(2)若为数列的前项和，

求数列的通项公式．

17．解：因为，

　　　　 所以，

　　　　 即，

　　　　 得，而，

　　　　 则，即，

　　　　 所以．

17．(本小题满分8分)

　　 解关于的不等式，其中．