
12.(13分) 已知曲线C: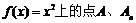 的横坐标分别为1和
的横坐标分别为1和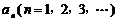 ,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且
,且a1=5,数列{xn}满足xn+1 = tf (xn – 1) + 1(t > 0且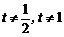 ).设区间
).设区间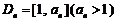 ,当
,当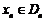 时,曲线C上存在点
时,曲线C上存在点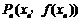 使得xn的值与直线AAn的斜率之半相等.
使得xn的值与直线AAn的斜率之半相等.
(1) 证明: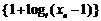 是等比数列;
是等比数列;
(2) 当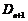
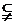
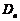 对一切
对一切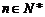 恒成立时,求t的取值范围;
恒成立时,求t的取值范围;
(3) 记数列{an}的前n项和为Sn,当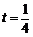 时,试比较Sn与n + 7的大小,并证明你的结论.
时,试比较Sn与n + 7的大小,并证明你的结论.
11.(13分) 已知点A,B的坐 标分别是(0,–1),(0,1),直线AM,BM相交于点M,且它们的斜率之积为
标分别是(0,–1),(0,1),直线AM,BM相交于点M,且它们的斜率之积为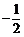 .
.
(1) 求点M的轨迹C的方程;
(2) 过D(2,0)的直线l与轨迹C有两个不同的交点时,求l的斜率的取值范围;
(3)
若过D(2,0),且斜率为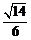 的直线l与(1)中的轨迹C交于不同的
的直线l与(1)中的轨迹C交于不同的 E、F(E在D、F之间),求
E、F(E在D、F之间),求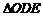 与
与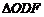 的面积之比.
的面积之比.
10.(13分) 已知函数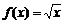 ,
,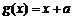 (a > 0)
(a > 0)
(5)
求a的值,使点M(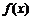 ,
, 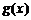 )到直线
)到直线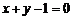 的最短距离为
的最短距离为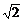 ;
;
(6)
若不等式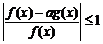 在
在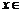 [1,4]恒成立,求a的取值范围.
[1,4]恒成立,求a的取值范围.
9.(12分) 已知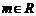 ,
,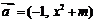 ,
,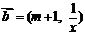 ,
,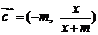 .
.
(3) 当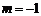 时,求使不等式
时,求使不等式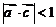 成立的x的取值范围;
成立的x的取值范围;
(4) 当m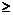 1时,求使不等式
1时,求使不等式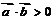 成立的x的取值
成立的x的取值 范围.
范围.
8.(12分) 已知向量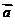
 与
与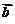 的夹角为30°,且 |
的夹角为30°,且 |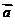 |=
|=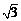 ,|
,|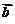 |=1,
|=1,
(1) 求 |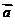 -2
-2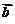 |的值;
|的值;
(2) 设向量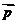 =
=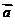 +2
+2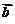 ,
,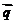 =
=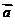 -2
-2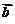 ,求向量
,求向量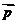 在
在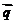 方向上的投影.
方向上的投影.
7.(12分) 在△ABC中,|AB|=|AC|,∠A =120°,A(0,2),BC所在直线方程为
x-y-1=0,求边AB、AC所在直线方程.
6. (本题满分12分)已知函数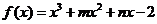 的图象过点(-1,-6),且函数
的图象过点(-1,-6),且函数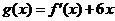 的图象关于y轴对称.
的图象关于y轴对称.
(Ⅰ)求m、n的值及函数y=f(x)的单调区间;
(Ⅱ)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
5. (本题满分12分)设函数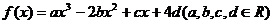 为奇函数,且
为奇函数,且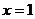 时,
时,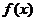 取极小值
取极小值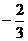 .
.
(Ⅰ)求函数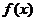 的解析式;
的解析式;
(Ⅱ)当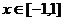 时,函数
时,函数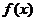 图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论?
图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论?
(Ⅲ)若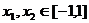 ,
, 求证:
求证: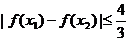 .
.
4. (本题满分12分) 如图,直三棱柱ABC-A1B1C1侧棱长为2,底面边AC、BC的长均为2,且AC⊥BC,若D为BB1的中点,E为AC的中点,M为AB的中点,N为BC的中点.
|
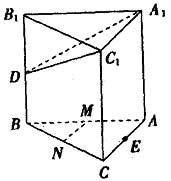 (2)求点E到平面A1C1D的距离;
(2)求点E到平面A1C1D的距离;
(3)求二面角C1-A1D-B1的大小.
3.已知函数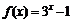 的反函数
的反函数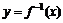 ,
,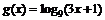
(1)若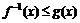 ,求
,求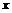 的取值范围
的取值范围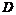 ;
;
(2)设函数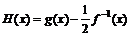 ,当
,当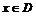 时,求
时,求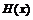 的值域.(本题满分12分)
的值域.(本题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com