
2.某蛋白质由m条肽链、n个氨基酸组成。该蛋白质至少有氧原子的个数是
A. n-m B. n-2m C. n+m D. n+2m
1.下列关于组成细胞有机物的叙述中,正确的是
A.淀粉和糖元的基本单位都是葡萄糖
B.多肽链在核糖体上一旦形成便具有生物活性
C.细胞核内的核酸只含脱氧核糖,细胞质中的核酸只含核糖
D.质量相同的糖、脂肪、蛋白质氧化分解所释放的能量是相同的
4. [巩固]D; 5. [巩固]A,6. [巩固]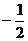 , 7. [迁移]
, 7. [迁移]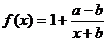 ,当a>b时在(
,当a>b时在(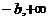 )上递减,∴
)上递减,∴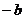 ≤-1,即a>b≥1; 若变为“闭”则a>b>1;8. [巩固]
≤-1,即a>b≥1; 若变为“闭”则a>b>1;8. [巩固] 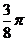 ,[迁移]满足条件的函数图象在y轴的右侧要“拐弯”,即对称轴在y轴的右侧,a<0
,[迁移]满足条件的函数图象在y轴的右侧要“拐弯”,即对称轴在y轴的右侧,a<0
8.函数图象的几种变换:平移变换、伸缩变换遵循“图进标退”原理:即曲线(函数图象)向上(右)平移m(m>0)个单位,则方程(表达式)中的y(x)应变为y-m(x-m); 曲线(函数图象)横(纵)坐标变为原来的n倍,则方程(表达式)中的x(y)应变为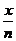 (
(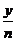 )。对称(翻折)变换,如函数y=f(-x)的图象是由y=f(x)的图象沿y轴翻折得到,y=-f(x)的图象是由y=f(x)的图象沿x轴翻折得到, y=|f(x)|
的图象是由y=f(x)的图象保留x轴上方的部分并翻折x轴下方的部分得到,y=f(|x|)是由y=f(x)的图象保留y轴右侧的部分,擦去左侧部分并将右侧的部分沿y轴翻折得到。记住两个函数图象:y=|x-a|的图象是“V字形”,“尖顶”是(a,0);
)。对称(翻折)变换,如函数y=f(-x)的图象是由y=f(x)的图象沿y轴翻折得到,y=-f(x)的图象是由y=f(x)的图象沿x轴翻折得到, y=|f(x)|
的图象是由y=f(x)的图象保留x轴上方的部分并翻折x轴下方的部分得到,y=f(|x|)是由y=f(x)的图象保留y轴右侧的部分,擦去左侧部分并将右侧的部分沿y轴翻折得到。记住两个函数图象:y=|x-a|的图象是“V字形”,“尖顶”是(a,0);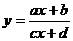 的图象是由一个反比例函数平移(分离常数)而来。
的图象是由一个反比例函数平移(分离常数)而来。
[举例]奇函数y=f(x) (x≠0 ) ,当x∈(0,+∞)时,f (x)=x-1 ,则函数f(x-1)的图象是( )
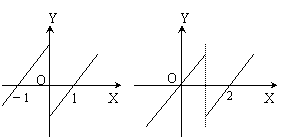
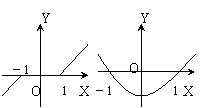
A B C D
解析:函数y=f(x)的图象为C图,将y=f(x)的图象向右平移1个单位即得到函数f(x-1)的图象,故选D。
[巩固] 函数f(x)=sin2x+2cos2x的图象向右平移m个单位后为偶函数,则最小正数m的值为___________
[迁移]使得函数y=x2+a|x|有四个单调区间的a的取值范围 。
简答
7.判断函数的单调性可用有关单调性的性质(如复合函数单调性的“同增异减”法则),研究三次或三次以上的多项式函数的单调性多用导数;证明函数单调性只能用定义或导数,不能用关于单调性的任何性质,用定义证明函数单调性的关键步骤往往是因式分解。记住并会证明:函数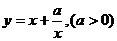 的单调性。了解单调性定义的变形:对区间[a,b]内的任意x,y都有
的单调性。了解单调性定义的变形:对区间[a,b]内的任意x,y都有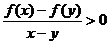 ,则函数f(x)在[a,b]递增(小于0则递减)。
,则函数f(x)在[a,b]递增(小于0则递减)。
[举例1]证明函数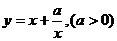 在(0,
在(0,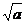
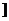 上递减,在
上递减,在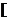
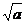 ,
,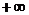 )上递增。
)上递增。
解析:记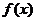 =
=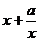 ,思路一:用定义证明,任取0<
,思路一:用定义证明,任取0<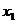 <
<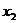 ≤
≤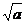 ,
,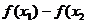 )=
)=
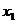 -
-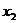 +
+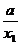 -
-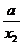 =(
=(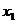 -
-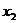 )(1-
)(1-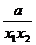 ),∵0<
),∵0<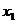 <
<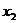 ≤
≤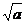 ,∴
,∴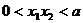 ,
,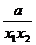 >1,
>1,
∴(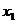 -
-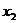 )(1-
)(1-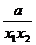 )>0,即
)>0,即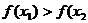 ),∴函数
),∴函数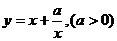 在(0,
在(0,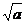
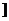 上递减.
上递减.
在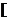
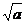 ,
,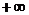 )上递增的证明留给读者自己完成。思路二:用导数,
)上递增的证明留给读者自己完成。思路二:用导数,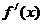 =1-
=1-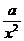 ,
,
若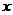 ∈(0,
∈(0,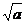
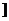 ,则
,则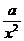 ≥1,
≥1,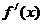 =1-
=1-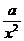 ≤0,∴函数
≤0,∴函数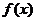 在(0,
在(0,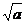
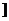 上递减.
上递减.
[举例2]函数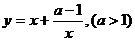 在区间(0,3)上单调递减,则a的取值范围为
在区间(0,3)上单调递减,则a的取值范围为
A.a≥10 B.1<a≤10 C.a≥4 D.1<a<4
解析:函数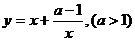 在区间(0,
在区间(0,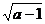
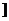 上递减,∴(0,3)是(0,
上递减,∴(0,3)是(0,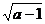
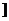 的子集,即3≤
的子集,即3≤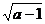 ,∴
,∴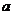 ≥10。
≥10。
[迁移]求函数f(x)=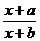 在(-1,
在(-1,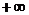 )单调递减的充要条件.
)单调递减的充要条件.
(如果把区间的左端变为“闭”,结果如何?)
6. 若函数f(x)满足:f(x+a)= f(x-a), 则f(x)是以2a为周期的函数。注意:不要和对称性相混淆。若函数f(x)满足:f(a+x)=-f(x)(a≠0),则f(x)是以2a为周期的函数。类似的条件还有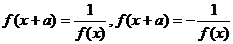 等。
等。
[举例]已知函数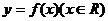 满足
满足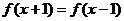 ,且当
,且当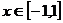 时,
时,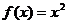 ,则
,则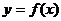 与
与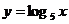 的图象的交点个数为
( )
的图象的交点个数为
( )
A、2 B、3 C、4 D、5
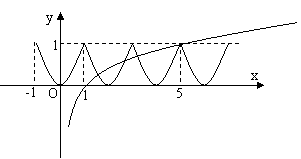 解析:由
解析:由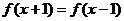 知函数
知函数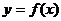 的周期为2,作出其图象如右,当x=5时,f(x)=1,log5x=1;
的周期为2,作出其图象如右,当x=5时,f(x)=1,log5x=1;
当x>5时,f(x)=1∈[0,1],
log5x>1, 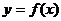 与
与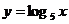 的图象不再有交点,故选C。
的图象不再有交点,故选C。
[巩固]设奇函数f(x)的定义域为R,且对任意实数x满足f(x+1)= -f(x),若当x∈[0,1]时,f(x)=2x-1,则f(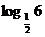 )= .
)= .
5. 偶函数图象关于y轴对称,推广:函数f(x)对定义域内的任意x都有f(a-x)=f(a+x)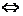 函数f(x)的图象关于x=a对称,再推广:
函数f(x)对定义域内的任意x都有f(a+x)=f(b-x),
函数f(x)的图象关于x=a对称,再推广:
函数f(x)对定义域内的任意x都有f(a+x)=f(b-x),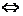 f(x)的图象关于x=
f(x)的图象关于x=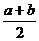 对称。奇函数图象关于原点对称,关推广:函数f(x)对定义域内的任意x都有f(a-x)=-f(a+x)
对称。奇函数图象关于原点对称,关推广:函数f(x)对定义域内的任意x都有f(a-x)=-f(a+x) 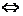 函数f(x)的图象关于(a,0)对称。注意:两个函数图象之间的对称问题不同于函数自身的对称问题。函数y=f(x)的图象关于直线x=a的对称曲线是函数y=f(2a-x)的图象,函数y=f(x)的图象关于点( a ,0)的对称曲线是函数y=-f(2a-x)的图象。,
函数f(x)的图象关于(a,0)对称。注意:两个函数图象之间的对称问题不同于函数自身的对称问题。函数y=f(x)的图象关于直线x=a的对称曲线是函数y=f(2a-x)的图象,函数y=f(x)的图象关于点( a ,0)的对称曲线是函数y=-f(2a-x)的图象。,
[举例1] 若函数y=f(x-1)是偶函数,则y=f(x)的图象关于 对称
解析:思路一:y=f(x-1)是偶函数,其图象关于y轴对称,向左平移1个单位后得到函数y=f(x)的图象,对称轴也随之平移至x=-1,即函数y=f(x)的图象关于x=-1对称;
思路二:y=f(x-1)是偶函数,则有f(-x-1)=f(x-1),由轴对称的等价定义知函数y=f(x)的图象关于x=-1对称。
[举例2]若函数f(x)=(x-a)3满足f(1+x)=-f(1-x),则f(2)= .
解析:由f(1+x)=-f(1-x)知,函数y=f(x)的图象关于(1,0)对称,事实上函数f(x)=(x-a)3的图象关于(a,0)对称,∴a=1,于是f(x)=(x-1)3,f(2)=1。
[巩固]函数y=f(a+x)与函数y=f(a-x)的图象
A.关于y轴对称 B.关于直线x=a对称
C.关于点M(a,0)对称 D. 关于点M(-a,0)对称
4.奇函数对定义域内的任意x满足f(-x)+f(x)=0;偶函数对定义域内的任意x满足f(-x)-f(x)=0;注意:使用函数奇偶性的定义解题时,得到的是关于 x的恒等式而不是方程。若函数f(x)是奇函数或偶函数,则f(x)定义域必关于原点对称;反之,函数定义域不关于原点对称,该函数既非奇函数也非偶函数。若f(x)是奇函数且f(0)存在,则f(0)=0;反之不然。
[举例]函数f(x)=loga|x-b|是偶函数的充要条件为
解析:思路一:函数f(x)=loga|x-b|是由偶函数y=loga|x|平移所得,∴函数f(x)=loga|x-b|的图象关于直线x=b对称,而它自身又是偶函数,图象又关于y轴(x=0)对称,∴b=0。
思路二:f(x)=loga|x-b|是偶函数则loga|-x-b|= loga|x-b|恒成立,即|x+b|=|x-b|恒成立,∴b=0。
[巩固] 设f(x)=lg(10x+1)+ax是偶函数,g(x)=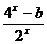 是奇函数,那么a+b的值为( )
是奇函数,那么a+b的值为( )
A.1
B.-1
C.-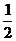 D.
D. 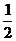
3.原函数的定义域是反函数的值域,原函数的值域是反函数的定义域;原函数与反函数的图象关于y=x对称;若函数y=f(x)的定义域为A,值域为C,a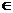 A,b
A,b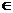 C,f [f-1(b)]=b; f-1[f(a)]=a
C,f [f-1(b)]=b; f-1[f(a)]=a
[举例1] 已知函数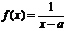 的反函数
的反函数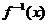 的图象的对称中心是(0,2),则a=____
的图象的对称中心是(0,2),则a=____
解析:原函数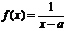 是有反比例函数(奇函数)平移而来,其图象关于(a,0)对称,∴它的反函数
是有反比例函数(奇函数)平移而来,其图象关于(a,0)对称,∴它的反函数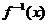 的图象应关于(0,a)对称,即a=2
的图象应关于(0,a)对称,即a=2
[举例2]已知f(x)=x2+2x+3,(x>-1),则f-1(3)= 。
解析:此题不宜求反函数(麻烦),注意到3是反函数y=f-1(x)的自变量,就是原函数y=f(x)的函数值,令x2+2x+3=3,得x=0或x=-2,又 x>-1,∴x=0,此即反函数的函数值f-1(3)(原函数的自变量)。
[迁移]已知f(x)=2sinxcosx+2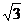 cos2x-
cos2x-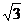 ,x
,x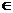 [
[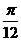 ,
,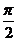 ],求f-1(1)的值。
],求f-1(1)的值。
2.求一个函数的反函数必须标明反函数的定义域,即要求出原函数的值域。求反函数的表达式的过程就是解(关于x的)方程的过程。注意:x=f-1(y)一定是唯一的。
[举例] 函数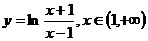 的反函数为
的反函数为
(A)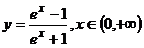 (B)
(B)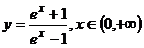 (C)
(C)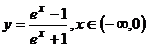 (D)
(D)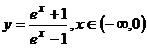
解析:∵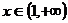 ,∴
,∴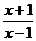 =1+
=1+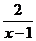 >1(关注分离常数),∴
>1(关注分离常数),∴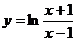 ∈(0,+
∈(0,+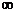 )
)
又由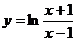 得
得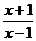 =
=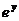 ,不难解出
,不难解出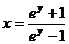 ,
,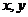 互换后得
互换后得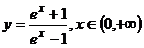
(互换是“全面”的,表达式上换,定义域、值域也要换)故选B。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com