
1、(1996)下列说法正确的是(N0表示阿伏加德罗常数的值) .
A 标准状况下,以任意比混和的甲烷和丙烷混和物22.4升,所含分子数为N0
B 标准状况下,1升辛烷完全燃烧后,所生成气态产物的分子数为8N0/22.4
C 常温常压下,活泼金属从盐酸中置换出1摩H2,发生转移的电子数为2N0
D 常温常压下,1摩氦气含有的核外电子数为4N0
33、[国家和国际组织常识]
材料一 为刺激美国经济增长,在美国总统奥巴马的强力敦促下,美国众议院2009年1月28日,以244票赞成、188票反对的表决结果通过了总额为8190亿美元的经济刺激方案。但方案在参议院遭到更强烈的抵制。2月11日,经过两天协商,国会参、众两院就经济刺激计划达成一致。两院经协商决定,将计划耗资削减到7890亿美元。
材料二 我国法律制定是在广泛听取社会各界意见的基础上,经过全国人大及其常委会多次审议,经过充分讨论后表决通过的。全国人民代表大会常务委员会第六次会议高票通过修改后的《中华人民共和国专利法》,国家主席签署第8号主席令予以公布,自2009年10月1日起施行。
结合材料,回答下列问题:
(1)结合材料一,简要分析美国产生这种政治现象的原因。(5 分)
(2)对比两则材料,说明我国国家权力运行原则的优越性。(5 分)
2009-2010学年度第一学期第二学段学情自主测评
32、(10分)[历史--历史上重大改革回眸]
材料一 史书记载,北魏孝文帝与心腹大臣拓跋澄讨论迁都洛阳的问题。孝文帝表示:“今日之行,诚知不易,但国家兴自北土,徙自平城,虽富有四海,文轨未一,此间用武之地,非可文治,移风易俗,信为甚难。崤函帝宅,河洛王里,因兹大举,光宅中原。”拓跋澄的回答是:“依洛中区,均天下所据,陛下制御华夏,辑平九服,苍生闻此,应当大庆。”
--《 魏书•拓跋澄传》
材料二
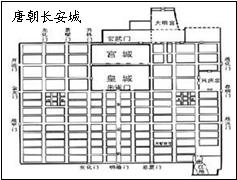
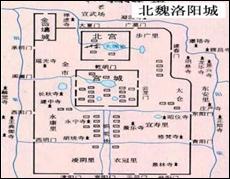
请回答:
(1)结合材料一分析孝文帝提出迁都的外部原因。(6分)
(2)结合上述材料说明孝文帝迁都洛阳产生的影响。(4分)
31.(10分)[地理一一环境保护]下面是“我国东部各省级行政区二氧化硫排放量图
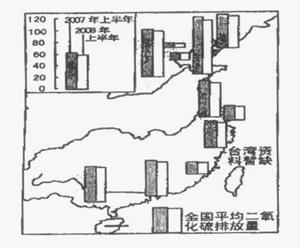
读图回答下列同题。
(1)比较图中我国东部地区南北方二氧化硫排放量的差异并分析原因。(6分)
(2)环境保护部发布公报,按环境管理的职能和性质进行分类.属于________管理。为减轻二氧化硫危害,请你从发展循环经济的角度为企业提出合理化建议。(4分)
30.(10分)[地理一自然灾害]
1983-1985年非洲经历了20世纪最大的一次干旱。从北到南有34个国家遭受大旱,其中24个国家发生了饥荒,1亿多人口受到饥饿的威胁。这次饥荒被联合国称为“非洲近代史上最大的人类灾难”。可怕的旱灾使一些地方的河流湖泊干涸。由于河口海水倒灌,非洲西部原本肥沃的良田变成了盐碱地,飞扬的黄沙淹埋了沙漠边缘的田园和牧场。此外,干旱还导致火灾频发,烧毁了树林和咖啡、可可种植园。1985年降水略有增多,蝗虫又铺天盖地地飞来。
结合材料回答下列问题:
(1)非洲多旱灾的原因是什么?
(2)干旱又引发了哪些自然灾害?试画一幅由干旱引发的灾害链示意图。
 材料三 1949年9月30日,中国人民政治协商会议第一次会议的代表们在天安门广场,挥铲为“人民英雄纪念碑”奠基,毛泽东当场宣读碑文:“三年以来,在人民解放战争和人民革命中牺牲的人民英雄永垂不朽!三十年以来,在人民解放战争和人民革命中牺牲的人民英雄们永垂不朽!由此上溯到一千八百四十年,从那时起,为了反对内外敌人,争取民族独立和人民自由幸福,在历次斗争中牺牲的人民英雄永垂不朽!”
材料三 1949年9月30日,中国人民政治协商会议第一次会议的代表们在天安门广场,挥铲为“人民英雄纪念碑”奠基,毛泽东当场宣读碑文:“三年以来,在人民解放战争和人民革命中牺牲的人民英雄永垂不朽!三十年以来,在人民解放战争和人民革命中牺牲的人民英雄们永垂不朽!由此上溯到一千八百四十年,从那时起,为了反对内外敌人,争取民族独立和人民自由幸福,在历次斗争中牺牲的人民英雄永垂不朽!”
(1)简析材料一中“鸦片战争是中国历史的转折”这句话的含义。(3分)
(2)结合所学知识,从中国现代化的角度,分析材料二中三次战争对中华民族的影响(12分)。
(3)①材料三中从“一千八百四十年”起,“为了反对内外敌人,争取民族独立和人民自由幸福”,中国人民开始学习西方,探索现代化之路。请仿照下例,另举两例(4分)。例:洋务运动学习西方科学技术,自强求富
② “三十年以来”,是中国共产党探索中国特色革命道路并取得了胜利的时期。试概说这“三十年”期间,中国共产党探索具有中国特色革命道路,并取得成功的事例两个。(4分)
(4)中华民族一百多年来浴血奋斗,写成了一部可歌可泣的历史,留下了许许多多的宝贵经验和惨痛的教训。这一切对于我们走现代化道路有什么启迪?(2分)
28、材料一:社会发展到一定程度,人们便开始返璞归真,城市人喜欢到农村找到难得的清静,这是社会发展的规律。返乡农民工王某通过调查发现,该村的自然生态良好,交通便利。王某依据上述规律,通过对当地情况的分析,预见到周边城市人周末开车到农村将成为其休闲的常态。于是他多渠道筹集资金,办起了生态果园,吸引了大批城市游客,为村民提供了三十余个就业岗位,带领村民一道走上了致富之路。
材料二:某地政府提出,要大力支持返乡农民工创业,加大信贷、税费减免等政策落实力度,鼓励和支持返乡农民工创业;加大创业指导服务力度,发放培训券加强培训,提供创业信息,找准创业路子;充分利用各种媒体和多种形式,大力宣传创业精神及各项政策,激发返乡农民工的创业热情。
(1)结合材料一,分析返乡农民工创业对农村经济发展的意义。(9 分)
(2)根据材料一,说明王某在创业的过程中是怎样在发挥主观能动性?(9 分)
(3)结合材料二,分析某地政府在促进返乡农民工创业过程中是如何履行职能的?(7 分)
4.复数包括实数和虚数,实数是虚部为0的复数;-1的“平方根”为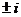 ,
, = -1,
= -1, ,
,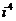 =1,
=1, ;复数运算遵循有理式的运算法则;复数的商一般将分母“实数化”(分子分母同乘分母的共扼复数);两个虚数不能比较大小;两个复数相等当且仅当它们的实部相等,虚部也相等;复数
;复数运算遵循有理式的运算法则;复数的商一般将分母“实数化”(分子分母同乘分母的共扼复数);两个虚数不能比较大小;两个复数相等当且仅当它们的实部相等,虚部也相等;复数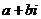 (
(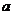 ∈R,
∈R, ∈R)在复平面内唯一对应点(
∈R)在复平面内唯一对应点(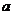 ,
, )。
)。
[举例1] 设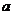 是实数,且
是实数,且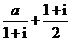 是实数,则
是实数,则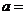 ( )
( )
A. B.
B.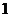 C.
C.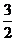 D.
D.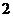
解析: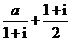 =
=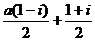 =
=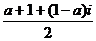 ∈R,则
∈R,则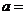 1
1
[举例2] 已知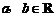 ,且
,且 (
(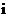 是虚数单位)是实系数一元二次方程
是虚数单位)是实系数一元二次方程
 的两个根,那么
的两个根,那么 的值分别是( )A
的值分别是( )A
A.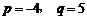 B.
B.
C.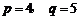 D.
D.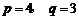
解析:分别将 代入方程得:
代入方程得: ①
①
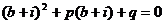 ②
对①②整理得:
②
对①②整理得:
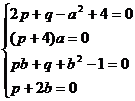 ;解得:
;解得: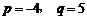 。本题也可以用“韦达定理”求解:
。本题也可以用“韦达定理”求解:
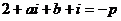 ③,
③,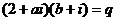 ④ 对③④整理得:
④ 对③④整理得:
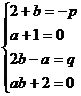
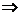
 。
。
[巩固1]在复平面内,复数z=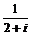 对应的点位于
对应的点位于
(A)第一象限 (B)第二象限 (C)第在象限 (D)第四象限
[巩固2] 设复数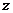 满足
满足 ,则
,则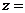 ( )
( )
A.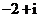 B.
B.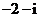 C.
C.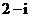 D.
D.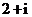
3.求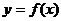 在闭区间内的最值的步骤:(1)求导数
在闭区间内的最值的步骤:(1)求导数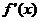 (2)求导数方程
(2)求导数方程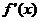 =0的根(3)检查
=0的根(3)检查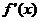 在根的左右值的符号,列表求得极值;也可通过解不等式
在根的左右值的符号,列表求得极值;也可通过解不等式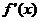 ≥0及
≥0及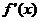 ≤0确定函数
≤0确定函数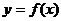 在给定区间内的单调情况,再确定函数的极值;最后将极值与区间端点的函数值比较以确定最值。
在给定区间内的单调情况,再确定函数的极值;最后将极值与区间端点的函数值比较以确定最值。
[举例1] 设函数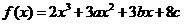 在
在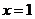 及
及 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;(Ⅱ)若对于任意的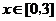 ,都有
,都有 成立,求c的取值范围.
成立,求c的取值范围.
解析:(Ⅰ)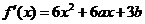 ,由
,由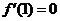 ,
,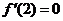 .解得
.解得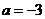 ,
,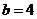 .
.
(Ⅱ) 在[0,3]上恒成立即
在[0,3]上恒成立即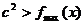 ,
,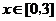
由(Ⅰ)可知, ,
,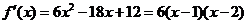 .
.
当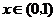 时,
时, ;当
;当 时,
时, ;当
;当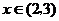 时,
时, .
.
即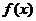 在
在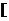 0,1]上递增,[1,2]上递减,[2,3]上递增;∴当
0,1]上递增,[1,2]上递减,[2,3]上递增;∴当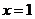 时,
时,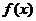 取得极大值
取得极大值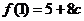 ,又
,又 .故当
.故当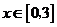 时,
时,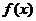 的最大值为
的最大值为 .
.
于是有: ,解得
,解得 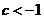 或
或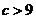 ,因此
,因此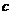 的取值范围为
的取值范围为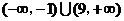 。
。
[举例2] 已知定义在正实数集上的函数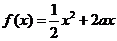 ,
, ,其中
,其中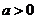 .设两曲线
.设两曲线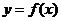 ,
,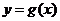 有公共点,且在该点处的切线相同.用
有公共点,且在该点处的切线相同.用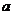 表示
表示 ,并求
,并求 的最大值;
的最大值;
解析:设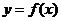 与
与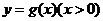 在公共点
在公共点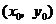 处的切线相同.
处的切线相同.
 ,
,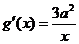 ,由题意
,由题意 ,
, .
.
即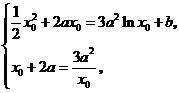 由
由 得:
得: ,或
,或 (舍去).
(舍去).
即有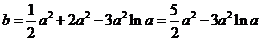 .
.
令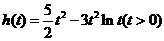 ,则
,则 .于是当
.于是当 ,即
,即 时,
时,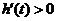 ;当
;当 ,即
,即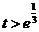 时,
时, .故
.故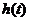 在
在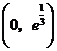 为增函数,
为增函数,
在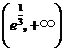 为减函数,∴
为减函数,∴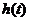 在
在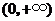 的最大值为
的最大值为 .
.
[巩固1] 设函数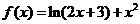 ,求
,求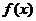 在区间
在区间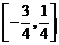 的最大值和最小值.
的最大值和最小值.
[巩固2] 已知函数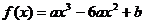 ,其图象为曲线C
,其图象为曲线C
(1) 直线l:y=x+1与曲线C相切于x轴上一点,求的a、b的值
(2)是否存在实数a、b,使f(x)在[-1、2]上取得最大值为3,最小值为-29。若存在,求出a、b的值,并指出函数y=f(x)的单调递增区间;若不存在,请说明理由。
2.“极值点”不是“点”,而是方程 的根。
的根。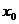 是函数
是函数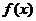 极值点则
极值点则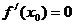 ;但是
;但是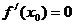 ,
,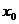 未必是极值点(还要求函数
未必是极值点(还要求函数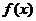 在
在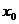 左右两侧的单调性相反);若
左右两侧的单调性相反);若
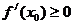 (或
(或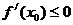 )恒成立,则函数
)恒成立,则函数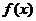 无极值。
无极值。
[举例1] 已知函数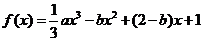 在
在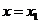 处取得极大值,在
处取得极大值,在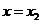 处取得极小值,且
处取得极小值,且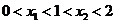 .(1)证明
.(1)证明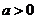 ;(2)若z=a+2b,求z的取值范围。
;(2)若z=a+2b,求z的取值范围。
解析:函数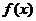 的导数
的导数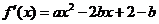 .
.
(Ⅰ)由函数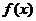 在
在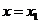 处取得极大值,在
处取得极大值,在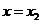 处取得极小值,知
处取得极小值,知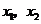 是
是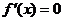 的两个根.所以
的两个根.所以 ;当
;当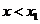 时,
时,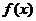 为增函数,
为增函数, ,由
,由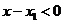 ,
,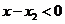 得
得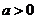 .
.
(Ⅱ)在题设下,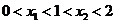 等价于
等价于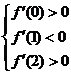 即
即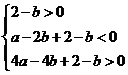 .
.
化简得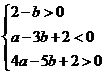 .此不等式组表示的区域为平面
.此不等式组表示的区域为平面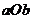 上三条直线:
上三条直线:
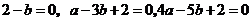 所围成的
所围成的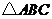 的内部,由“线性规划”的知识容易求得:
的内部,由“线性规划”的知识容易求得: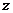 的取值范围为
的取值范围为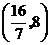 .
.
[举例2] 已知函数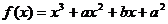 在
在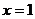 处有极值10,则
处有极值10,则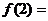
解析: 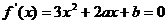 ,∴
,∴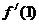 =
=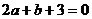 ①
①
 ② 由①②得:
② 由①②得: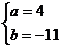 或
或
当 时,
时,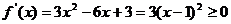 ,此时函数
,此时函数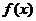 无极值,舍去;
无极值,舍去;
当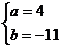 时
时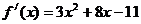 ,函数
,函数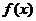 在
在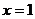 处左减右增,有极小值;
处左减右增,有极小值;
此时∴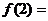 18 。注:在解决“已知函数的极值点求参变量”的问题时,为避免“增根”,需将求出的参变量的值代入
18 。注:在解决“已知函数的极值点求参变量”的问题时,为避免“增根”,需将求出的参变量的值代入 检验其是否为完全平方式,若是则函数无极值(单调),否则有极值;也可以对
检验其是否为完全平方式,若是则函数无极值(单调),否则有极值;也可以对 再次求导,看
再次求导,看 的值,为0则无极值,为正则有极小值,为负则有极大值。
的值,为0则无极值,为正则有极小值,为负则有极大值。
[巩固1]已知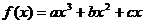 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间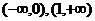 上是减函数,又
上是减函数,又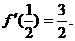 (Ⅰ)求
(Ⅰ)求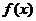 的解析式; (Ⅱ)若在区间
的解析式; (Ⅱ)若在区间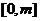 (m>0)上恒有
(m>0)上恒有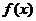 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
[举例2]设函数 ,其中
,其中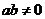 .证明:当
.证明:当 时,函数
时,函数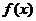 没有极值点;当
没有极值点;当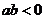 时,函数
时,函数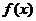 有且只有一个极值点,并求出极值.(07高考山东文21)
有且只有一个极值点,并求出极值.(07高考山东文21)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com