
2.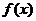 是偶函数,且当
是偶函数,且当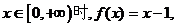 则不等式
则不等式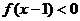 的解集是( )
的解集是( )
A.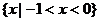 B.
B.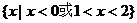
C.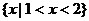 D.
D.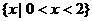
1.命题“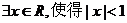 ”的否定是 ( )
”的否定是 ( )
A.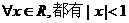 B.
B.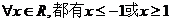
C.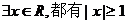 D.
D.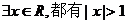
22.解:(1)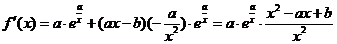
令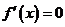 得
得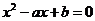
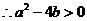 又
又 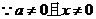
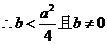 ………………4分
………………4分
(2)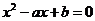 在
在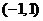 有两个不相等的实根.
有两个不相等的实根.
即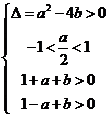 得
得 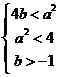
所以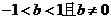 ………………8分
………………8分
(3)由①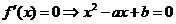
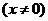
①当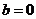 ,
,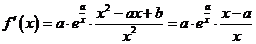 在
在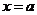 左右两边异号
左右两边异号
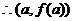 是
是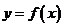 的唯一的一个驻点
的唯一的一个驻点
由题意知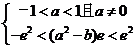 即
即 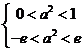 即
即 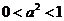
存在这样的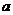 满足题意
满足题意
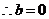 符合题意
………………10分
符合题意
………………10分
②当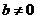 时,
时,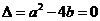 即
即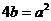
这时函数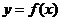 唯一的一个驻点为
唯一的一个驻点为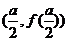
由题意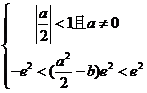
即 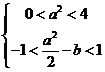 即
即 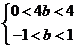
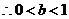 ………………………………14分
………………………………14分
综合①②知:满足题意
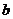 的范围为
的范围为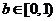 .
……………………………15分
.
……………………………15分
21.解:(1) 设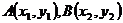
由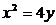 ,得
,得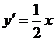
则过点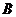 的切线方程为:
的切线方程为:
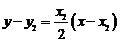 ,即
,即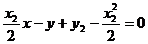
由已知: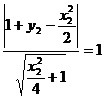 ,又
,又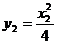 ,
,
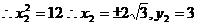 ,
,
即点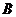 坐标为
坐标为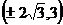 ,
,
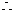 直线
直线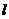 的方程为:
的方程为: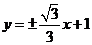 .
(7分)
.
(7分)
(Ⅱ)由已知,直线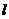 的斜率存在,则设直线
的斜率存在,则设直线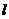 的方程为:
的方程为: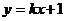 ,
,
联立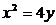 ,得
,得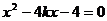
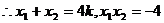
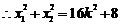 (9分)
(9分)
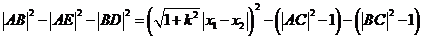 (11分)
(11分)
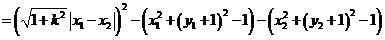

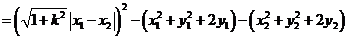
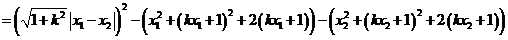 (13分)
(13分)
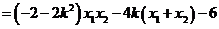 =
=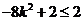
所以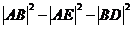 的取值范围是
的取值范围是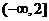 。
(15分)
。
(15分)
20、解:
(1)当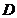 为
为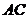 中点时,有
中点时,有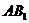 ∥平面
∥平面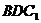 .…1分
.…1分
 证明:连结
证明:连结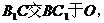 连结
连结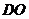 ,
,
∵四边形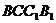 是矩形 ∴
是矩形 ∴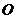 为
为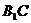 中点
中点
∵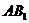 ∥平面
∥平面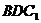 ,
,
且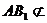 平面
平面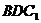 ,
,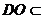 平面
平面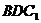
∴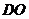 ∥
∥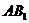 ,------------------5分
,------------------5分
∴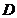 为
为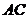 的中点.------------------6分
的中点.------------------6分
(2)建立空间直角坐标系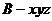 如图所示,
如图所示,
则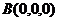 ,
,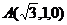 ,
,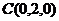 ,
,
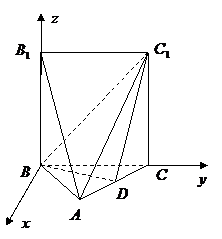
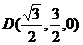 ,
,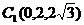 ------------8分
------------8分
所以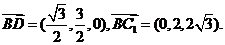
设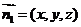 为平面
为平面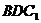 的法向量,
的法向量,
则有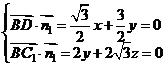 ,
,
即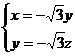
令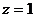 ,可得平面
,可得平面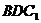 的一个
的一个
法向量为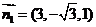 , ----------------11分
, ----------------11分
而平面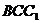 的法向量为
的法向量为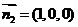 , ---------------------------12分
, ---------------------------12分
所以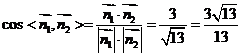 ,
,
所以二面角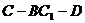 的余弦值为
的余弦值为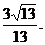 ----------------------------14分
----------------------------14分
19.(1)由条件: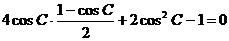
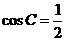 ………………(3分)
………………(3分)
故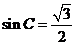 ,则
,则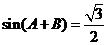 ,
,
由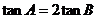 ,得
,得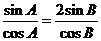 , 所以
, 所以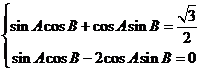 ,
,
得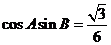 ,
, ,
,
所以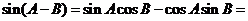
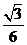 (7分)
(7分)
(2)由余弦定理: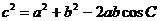
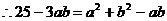
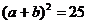
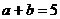
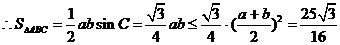
当且仅当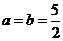 取得最大值.
(14分)
取得最大值.
(14分)
18.解:(1)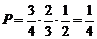 ;…………………………………………4分
;…………………………………………4分
(2)提示: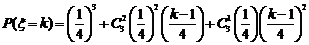 ,
,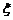 的分布列为:
的分布列为:
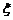 |
1 |
2 |
3 |
4 |
|
P |
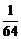 |
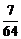 |
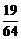 |
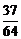 |
………………………………(建议对1个给2分)…………………………………………12分
故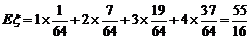 .………………………………………………14分
.………………………………………………14分
16.2016 17.②③
11.90 12.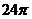 13.
13.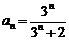 14.
14.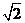 15.
15.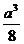
1.D 2.B 3.A 4.D 5.C 6.A 7.D 8.C 9.A 10.D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com