
6. [巩固1][-2,0],[巩固2]C,[迁移] (-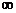 ,-6)
,-6)
4、[巩固1] 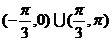 [巩固2]
[巩固2] 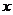 ∈
∈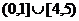 ;5、[巩固1]A,[巩固2]{1,2
;5、[巩固1]A,[巩固2]{1,2
2、[巩固]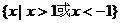 , [迁移](-2,2),3、[巩固1] C ,[巩固2] (-
, [迁移](-2,2),3、[巩固1] C ,[巩固2] (-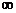 ,
,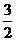
1、 [巩固1](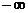 ,-1)∪(0,1),[巩固2] 当a=0时不等式的解为:{x|x<1};当a>0时不等式的解为:{x|
,-1)∪(0,1),[巩固2] 当a=0时不等式的解为:{x|x<1};当a>0时不等式的解为:{x|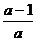 <x<1};当a<0时不等式的解为:{x|x<1或x>
<x<1};当a<0时不等式的解为:{x|x<1或x>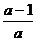 };[迁移]9。
};[迁移]9。
6. 遇到含参不等式恒成立求参变量的范围问题,通常采用分离参数法,转化为求某函数的最大值(或最小值);具体地:g(a)>f(x)在x∈A上恒成立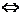 g(a)>f(x)max,g(a)<f(x)在x∈A上恒成立
g(a)>f(x)max,g(a)<f(x)在x∈A上恒成立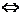 g(a)<f(x)min,(x∈A)。当参变量难以分离时,也可以用:f(a,x)>0在x∈A上恒成立
g(a)<f(x)min,(x∈A)。当参变量难以分离时,也可以用:f(a,x)>0在x∈A上恒成立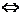 f(a,x)min>0, (x∈A)及f(a,x)<0在x∈A上恒成立
f(a,x)min>0, (x∈A)及f(a,x)<0在x∈A上恒成立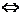 f(a,x)max>0, (x∈A)来转化;还可以借助于函数图象解决问题。特别关注:“不等式f(a,x)≥0对所有x∈M恒成立”与 “不等式f(a,x)≥0对所有a∈M恒成立”是两个不同的问题,前者是关于x的不等式,而后者则应视为是关于a的不等式。特别提醒:“判别式”只能用于“二次函数对一切实数恒成立”的问题,其它场合,概不适用。
f(a,x)max>0, (x∈A)来转化;还可以借助于函数图象解决问题。特别关注:“不等式f(a,x)≥0对所有x∈M恒成立”与 “不等式f(a,x)≥0对所有a∈M恒成立”是两个不同的问题,前者是关于x的不等式,而后者则应视为是关于a的不等式。特别提醒:“判别式”只能用于“二次函数对一切实数恒成立”的问题,其它场合,概不适用。
[举例1]定义在R上的函数f(x)为奇函数,且在[0,+
 为增函数,对任意
为增函数,对任意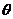 ∈R,不等式f(cos2
∈R,不等式f(cos2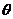 -3)+f(2m-sin
-3)+f(2m-sin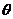 )>0恒成立,则实数m的取值范围是
)>0恒成立,则实数m的取值范围是
解析:∵函数f(x)为奇函数且在[0,+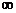
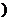 为增函数,易见:函数f(x)为在(-
为增函数,易见:函数f(x)为在(-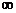 ,0
,0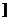 上递增,∴函数f(x) 在(-
上递增,∴函数f(x) 在(-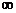 ,+
,+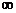
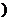 上递增;不等式f(cos2
上递增;不等式f(cos2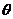 -3)+f(2m-sin
-3)+f(2m-sin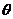 )>0恒成立
)>0恒成立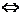
不等式f(cos2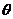 -3)>f(-2m+sin
-3)>f(-2m+sin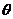 )恒成立
)恒成立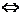 不等式cos2
不等式cos2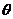 -3>-2m+sin
-3>-2m+sin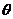 恒成立
恒成立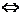
2m>2sin2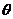 + sin
+ sin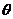 +2恒成立,记g(
+2恒成立,记g(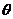 )=2sin2
)=2sin2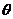 + sin
+ sin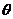 +2=2(sin
+2=2(sin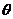 +
+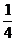 )2+
)2+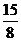 , g(
, g(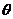 )max=g(1)=5
)max=g(1)=5
∴2m>5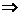 m>
m>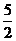 .
.
[举例2]设奇函数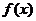 在[-1,1]上是增函数,且
在[-1,1]上是增函数,且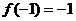 ,若函数
,若函数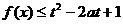 对所有的
对所有的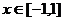 及所有的
及所有的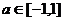 都成立,则
都成立,则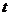 的取值范围是
;
的取值范围是
;
解析:先视x为主元,关于x的不等式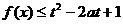 对所有的
对所有的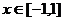 横成立
横成立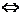
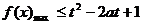 ,又
,又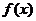 在[-1,1]上递增,∴
在[-1,1]上递增,∴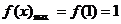 ,即:
,即:
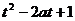 ≥1,现在视a为主元,关于a的不等式
≥1,现在视a为主元,关于a的不等式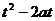 ≥0对所有的
≥0对所有的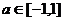 都成立,
都成立,
记g(a)= -2ta+t2,此时分离参数(t)或求函数g(a)的最小值均需讨论,但如果注意到函数g(a)是一次函数,其图象是一条直线,则g(-1) ≥0且g(1) ≥0得t≥2或t≤-2或t=0。
[巩固1]f(x)是偶函数,且f(x)在[0,+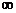
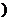 上是增函数,如果f(ax+1)≤f(x-2)在[
上是增函数,如果f(ax+1)≤f(x-2)在[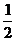 ,1]上恒成立,则实数a的取值范围是
。
,1]上恒成立,则实数a的取值范围是
。
[巩固2]]对满足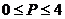 的实数P,做
的实数P,做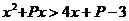 恒成立的x的取值范围是: A.
恒成立的x的取值范围是: A.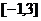 B.
B.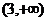 C.
C.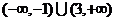 D.
D.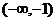
[迁移]已知函数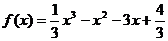 ,直线
,直线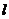 :
: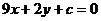 ,若当
,若当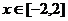 时,函数
时,函数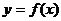 的图象恒在直线
的图象恒在直线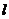 的下方,则
的下方,则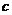 的取值范围是
的取值范围是
简答
5.解决含参变量的无理不等式、含参变量的绝对值不等式、含参变量的指(对数)数不等式问题时常用数形结合。
 [举例1]不等式
[举例1]不等式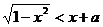 在[-1,1]上恒成立,
在[-1,1]上恒成立,
则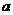 的取值范围是
的取值范围是
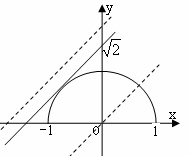
解析:分别作函数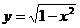 和
和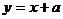 的图象如右,
的图象如右,
前者是以原点为圆心的单位圆的上半部分,后者是斜率
为1的直线。不等式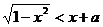 的解即半圆在直线
的解即半圆在直线
的下方的点的横坐标;不等式恒成立即半圆都在直线的下
方,由图可见,只需直线在与圆相切的位置的上方,即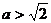 。
。
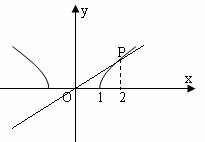
|
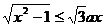 的解集为[1,2],则
的解集为[1,2],则
实数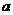 的取值集合是
的取值集合是
解析:分别作函数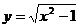 和
和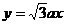 的图象如右,
的图象如右,
前者是双曲线x2-y2=1的x轴上方的部分,后者是过原点
的直线。不等式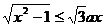 的解即双曲线在直线下方
的解即双曲线在直线下方
的点的横坐标;如图所示,不等式的解集为[1,2],即两图象交点P的横坐标为2,分别代入两函数表达式,得: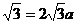 ,即
,即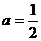 .
.
[巩固1]不等式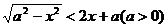 的解集是( )
的解集是( )
A 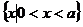 B
B 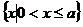 C
C 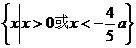 D
D 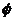
[巩固2]关于x的不等式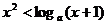 在(0,1)上恒成立,则a的取值范围是 。
在(0,1)上恒成立,则a的取值范围是 。
4.解抽象函数的不等式离不开函数的单调性。抽象函数的不等式反映出的函数值的大小,需借助于函数的单调性化归为自变量的大小,特别注意定义域。画抽象函数的“概念图”是化抽象为形象的有效途径;对某些有具体函数背景的抽象函数,可以从该具体函数中寻找解题线索。
[举例1]已知奇函数f(x)在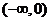 为减函数,f(2)=0则不等式(x-1)f(x-1)<0的解集为:
为减函数,f(2)=0则不等式(x-1)f(x-1)<0的解集为:
 。
。
解析:作函数f(x)的“概念图”如右:
先求不等式xf(x)<0的解:当x>0时
(y轴右侧),f(x)<0(x轴下方),
∴x>2;当x<0时(y轴左侧),
f(x)>0(x轴下方),∴x<-2;可见
不等式xf(x)<0的解为:x<-2或x>2
(也可以根据满足不等式xf(x)<0的函数图象上的点横、纵坐标异号,看图象在第二、四象限的部分得出)。再将x换成x-1,得:x-1<-2或x-1>2即x<-1或x>3。
[举例2]已知函数f(x)对任意实数x、y均有f(x+y)+2=f(x)+f(y),且当x>0时,f(x)>2,f(3)=5,求不等式 f(a2-2a-2)<3的解.
解析:正比例函数f(x)满足:f(x+y)=f(x)+f(y),本题中函数f(x)可视为一次函数。解抽象函数的不等式,需知函数的单调性;用定义:任取x1<x2,x2-x1>0,则f(x2-x1)>2
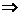 f(x2)+f(-x1)-2>2
f(x2)+f(-x1)-2>2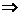 f(x2)+f(-x1)>4;对f(x+y)+2=f(x)+f(y)取x=y=0得:f(0)=2,再取y= -x
f(x2)+f(-x1)>4;对f(x+y)+2=f(x)+f(y)取x=y=0得:f(0)=2,再取y= -x
得f(x)+f(-x)=4即f(-x)=4-f(x),∴有f(x2)+4-f(x1)>4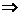 f(x2) > f(x1)
f(x2) > f(x1) 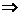 f(x)在R上递增
f(x)在R上递增
又f(3)=f(2)+f(1)-2=f(1)+f(1)-2+f(1)-2=3f(1)-4=5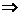 f(1)=3;于是:不等式 f(a2-2a-2)<3
f(1)=3;于是:不等式 f(a2-2a-2)<3
等价于f(a2-2a-2)<f(1)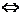 a2-2a-2<1
a2-2a-2<1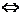 -1<a<3。
-1<a<3。
注:(ⅰ)已知抽象函数的运算性质,常用“赋值法”。
(ⅱ)有具体函数背景的抽象函数问题,如果是客观题,可以用具体函数求解。如本题:可设f(x)=kx+b,根据条件求出k、b,再解不等式。
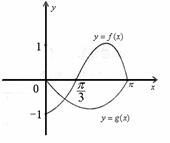 [巩固1]
[巩固1] 是
是
奇函数,它们的定义域均为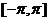 ,且
,且
它们在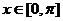 上的图象如图所示,则
上的图象如图所示,则
不等式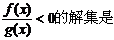
[巩固2]已知定义在正实数集上的函数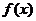 满足①若
满足①若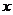 >1,则
>1,则 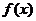 <0;②
<0;②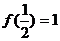 ;③对定义域内的任意实数
;③对定义域内的任意实数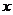 ,
,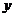 ,都有:
,都有: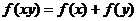 ,则不等式
,则不等式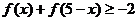
的解集为 。
3.分段函数形成的不等式一般分段解,再取并集;对较为复杂的分段函数问题可以借助于图象解决。
[举例1]设函数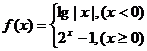 ,若
,若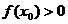 则x0取值范围是 ( )
则x0取值范围是 ( )
A.(-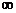 ,-1)∪(1,+
,-1)∪(1,+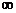 ) B.(-
) B.(-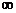 ,-1)∪(0,+
,-1)∪(0,+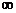 )
)
C.(-1,0)∪(0,1) D.(-1,0)∪(0,+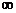 )
)
解析:若x0<0,则f(x0)=lg|x0|>0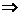 |x0|>1
|x0|>1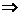 x0<-1;若x0≥0,则f(x0)=
x0<-1;若x0≥0,则f(x0)=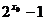 >0
>0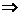 x0>0
x0>0
故选B
[举例2]已知:函数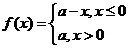 (
(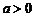 ).解不等式:
).解不等式: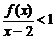 .
.
解析:(ⅰ)当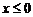 时,即解
时,即解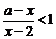
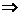
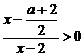 ,此时不等式恒成立,即
,此时不等式恒成立,即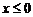 ;
;
(ⅱ)当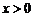 时,即解
时,即解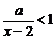
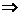
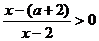 ,∵
,∵ 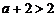 ,
,
∴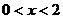 或
或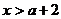 .综上:不等式的解为:
.综上:不等式的解为: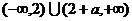
[巩固1]设函数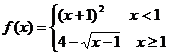 ,则使
,则使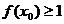 。则x0的取值范围是( )
。则x0的取值范围是( )
A (-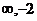 ]
]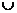 [0,10] B (-
[0,10] B (-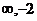 ]
]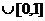 C (
C (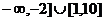 D[-2,0]
D[-2,0] [1,10]
[1,10]
[巩固2]已知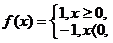 则不等式
则不等式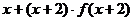 ≤5的解集是
≤5的解集是

2.解绝对值不等式的关键是“去绝对值”,通常有①利用绝对值不等式的性质:若M>0则
|f(x)|>M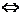 f(x)>M或f(x)<-M;②平方(不等式两边同正);③讨论(绝对值内的式子为0)。
f(x)>M或f(x)<-M;②平方(不等式两边同正);③讨论(绝对值内的式子为0)。
[举例]设p:x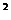 -x-20>0,q:
-x-20>0,q: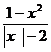 <0,则p是q的 ( )
<0,则p是q的 ( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
解析:p:(-∞,-4) ∪(5,+∞);以下对命题q中的不等式去绝对值:(ⅰ)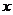 ≥0时
≥0时
原不等式等价于: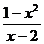 <0
<0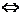
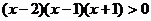
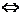 -1<
-1<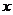 <1或
<1或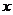 >2;注意到
>2;注意到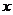 ≥0,
≥0,
∴0≤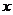 <1或
<1或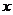 >2;(ⅱ)
>2;(ⅱ)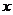 <0时,原不等式等价于:
<0时,原不等式等价于: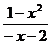 <0
<0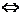
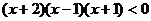
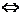 -1<
-1<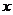 <1或
<1或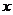 <-2;注意到
<-2;注意到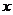 <0, ∴-1<
<0, ∴-1<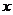 <0或
<0或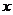 <-2;∴q:(-∞,-2)∪(-1,1)∪(2,+∞)
<-2;∴q:(-∞,-2)∪(-1,1)∪(2,+∞)
可见:p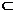 q,故选A。
q,故选A。
[巩固]不等式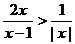 的解集是
.
的解集是
.
[迁移]已知函数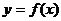 在
在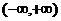 上是增函数,A (0, -2 ), B (4 ,2 )是其图象
上是增函数,A (0, -2 ), B (4 ,2 )是其图象
上的两个点,那么不等式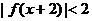 的解集是
的解集是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com