
3.解:(1)原不等式等价于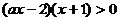
①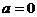 时
时 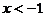 ②
②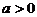 时
时 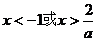
由于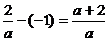 ,于是当
,于是当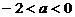 时
时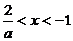
③ 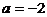 时解集为空集
时解集为空集 ④
当
④
当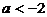 时
时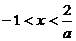
(2)∵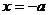 时,不等式成立 ∴
时,不等式成立 ∴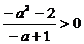 即
即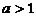
冲刺强化训练(4)
2.解:(1)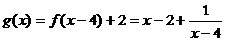
(2)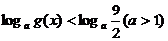
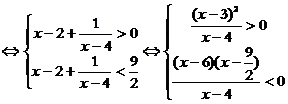
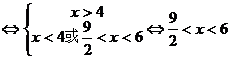
∴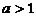 时原不等式的解集为
时原不等式的解集为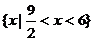
1. 解:原不等式可化为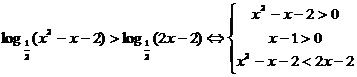
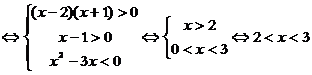
1、B 2、B 3、C 4、-2 (-5,5) 5、(-1,0)
[例题探究]
9.已知函数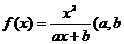 为常数),且方程
为常数),且方程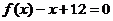 有两个实根为
有两个实根为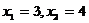 .
.
(1)求函数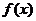 的解析式;
的解析式;
(2)设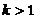 ,解关于
,解关于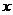 的不等式
的不等式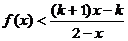 .
.
第4讲 解不等式
[课前热身]
8.记函数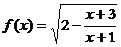 的定义域为A,
的定义域为A,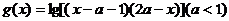 的定义域为B,(1)求A ; (2)若
的定义域为B,(1)求A ; (2)若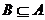 ,求实数
,求实数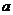 的范围.
的范围.
7.解关于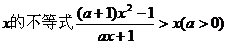
6.定义“符号函数”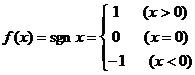 ,则不等式
,则不等式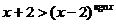
的解集为 .
5.如果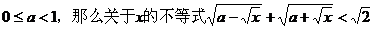 的解集是
的解集是
4.关于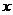 的不等式
的不等式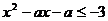 的解集不为空集,则实数
的解集不为空集,则实数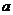 的取值范围为
。
的取值范围为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com