
15.解:(1)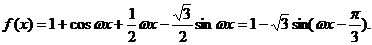
由函数的图象及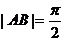 ,得函数的周期
,得函数的周期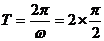 ,解得
,解得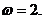
(2)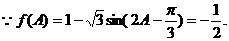
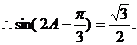
又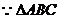 是锐角三角形,
是锐角三角形,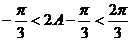 ,
,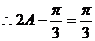 ,即
,即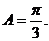
由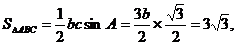 得
得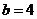 由余弦定理,得
由余弦定理,得
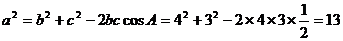 ,即
,即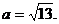
16(1)∵切线在x轴,y轴上的截距的绝对值相等,
∴切线的斜率是±1. ----------------------2分
分别依据斜率设出切线的斜率,用点到直线的距离公式,或△法,解得切线的方程为:
x+y-3=0, ----------------------4分
x+y+1=0, ----------------------5分
x-y+5=0, ----------------------6分
x-y+1=0. ----------------------7分
(2)将圆的方程化成标准式(x+1)2+(y-2)2=2,圆心C(-1,2),半径r=,
∵切线PM与CM垂直,∴|PM|2=|PC|2-|CM|2,
又∵|PM|=|PO|,坐标代入化简得2x1-4y1+3=0. ----------------------10分
|PM|最小时即|PO|最小,而|PO|最小即P点到直线2x1-4y1+3=0的距离,即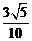 .
.
从而解方程组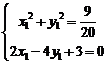 , ----------------------13分
, ----------------------13分
得满足条件的点P坐标为(-,). ----------------------14分
9.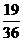 10.
10.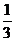 11.
11.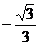 12.
12.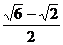 13.
13.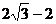 14.
14.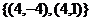
1.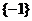 2.1 3.
2.1 3.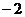 4.650 5.4 6.
4.650 5.4 6.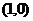 7.
7.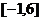 8.3:2
8.3:2
16. 已知圆C:x2+y2+2x-4y+3=0.(1)若C的切线在x轴,y轴上的截距的绝对值相等,求此切线方程;(2)从圆C外一点P(x1,y1)向圆引一条切线,切点为M,O为原点,且有|PM|=|PO|,求使|PM|最小的P点的坐标.
15.A、B是直线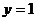 与函数
与函数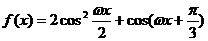
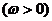 图象的两个相邻交点,且
图象的两个相邻交点,且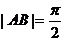 .(1)求
.(1)求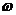 的值;(2)在锐角
的值;(2)在锐角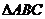 中,
中,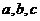 分别是角A,B,C的对边,若
分别是角A,B,C的对边,若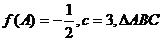 的面积为
的面积为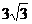 ,求
,求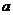 的值.
的值.
14.设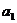 ,
,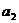 ,…,
,…,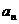 是各项不为零的
是各项不为零的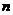 (
(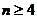 )项等差数列,且公差
)项等差数列,且公差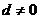 .若将此数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对
.若将此数列删去某一项后,得到的数列(按原来顺序)是等比数列,则所有数对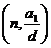 所组成的集合为____________.
所组成的集合为____________.
13.若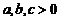 ,且
,且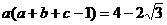 ,则
,则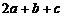 的最小值为 .
的最小值为 .
12.如图,已知椭圆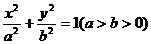 的左、右准线分别为
的左、右准线分别为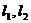 ,且分别交
,且分别交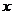 轴于
轴于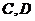 两点,从
两点,从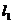 上一点
上一点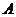 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点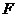 被
被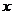 轴反射后与
轴反射后与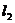 交于点
交于点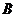 ,若
,若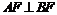 ,且
,且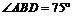 ,则椭圆的离心率等于
.
,则椭圆的离心率等于
.
11.若由不等式组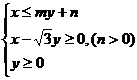 确定的平面区域的边界为三角形,且它的外接圆的圆心在
确定的平面区域的边界为三角形,且它的外接圆的圆心在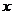 轴上,则实数
轴上,则实数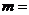 .
.
10.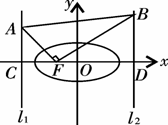 若
若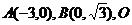 为坐标原点,点
为坐标原点,点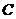 在第二象限内,且
在第二象限内,且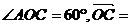
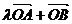 ,则实数
,则实数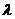 的值是
.
的值是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com