
(三)例题分析:
例1.(1)若一个等差数列前3项的和为34,最后三项的和为146,且所有项的和为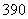 ,则这个数列有13 项;
,则这个数列有13 项;
(2)已知数列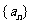 是等比数列,且
是等比数列,且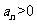 ,
,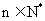 ,
,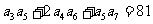 ,则
,则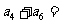 9 .
9 .
(3)等差数列前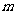 项和是
项和是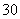 ,前
,前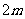 项和是
项和是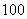 ,则它的前
,则它的前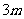 项和是 210 .
项和是 210 .
例2.若数列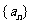 成等差数列,且
成等差数列,且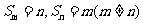 ,求
,求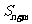 .
.
解:(法一)基本量法(略);
(法二)设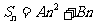 ,则
,则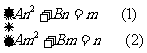
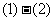 得:
得: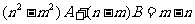 ,
,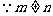 ,
∴
,
∴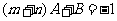 ,
,
∴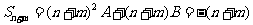 .
.
例3.等差数列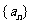 中共有奇数项,且此数列中的奇数项之和为
中共有奇数项,且此数列中的奇数项之和为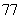 ,偶数项之和为
,偶数项之和为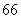 ,
,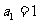 ,求其项数和中间项.
,求其项数和中间项.
解:设数列的项数为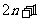 项,
项,
则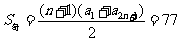 ,
,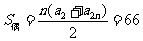
∴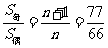 ,∴
,∴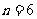 ,∴数列的项数为
,∴数列的项数为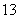 ,中间项为第
,中间项为第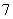 项,且
项,且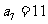 .
.
说明:
(1)在项数为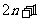 项的等差数列
项的等差数列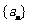 中,
中,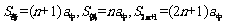 ;
;
(2)在项数为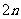 项的等差数列
项的等差数列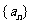 中
中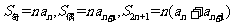 .
.
例4.数列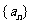 是首项为
是首项为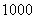 ,公比为
,公比为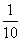 的等比数列,数列
的等比数列,数列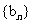 满足
满足
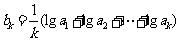
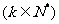 ,
,
(1)求数列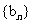 的前
的前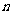 项和的最大值;(2)求数列
项和的最大值;(2)求数列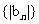 的前
的前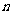 项和
项和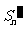 .
.
解:(1)由题意: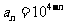 ,∴
,∴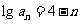 ,
,
∴数列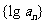 是首项为3,公差为
是首项为3,公差为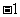 的等差数列,
的等差数列,
∴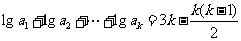 ,∴
,∴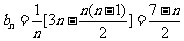
由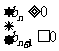 ,得
,得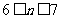 ,∴数列
,∴数列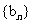 的前
的前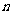 项和的最大值为
项和的最大值为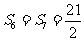
(2)由(1)当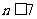 时,
时,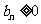 ,当
,当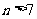 时,
时,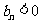 ,
,
∴当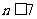 时,
时,
当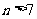 时,
时,
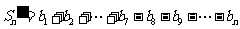
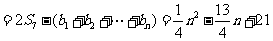
∴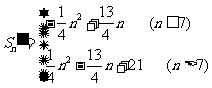 .
.
例5*.若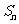 和
和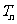 分别表示数列
分别表示数列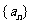 和
和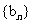 的前
的前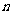 项和,对任意自然数
项和,对任意自然数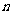 ,有
,有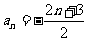 ,
,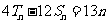 ,(1)求数列
,(1)求数列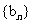 的通项公式;(2)设集合
的通项公式;(2)设集合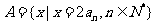 ,
,
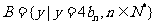 .若等差数列
.若等差数列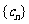 任一项
任一项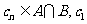 是
是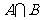 中的最大数,且
中的最大数,且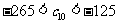 ,求
,求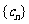 的通项公式.
的通项公式.
解:(1)当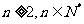 时:
时: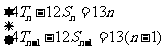 ,
,
两式相减得: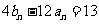 ,∴
,∴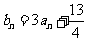
 ,又
,又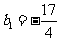 也适合上式,
也适合上式,
∴数列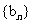 的通项公式为
的通项公式为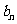
 .
.
(2)对任意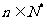 ,
,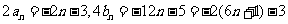 ,∴
,∴ ,∴
,∴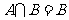
∵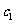 是
是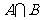 中的最大数,∴
中的最大数,∴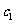
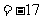 ,设等差数列
,设等差数列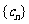 的公差为
的公差为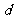 ,则
,则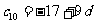 ,
,
∴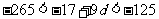 ,即
,即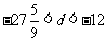 ,又
,又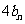 是一个以
是一个以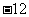 为公差的等差数列,
为公差的等差数列,
∴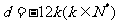 ,∴
,∴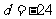 ,∴
,∴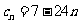 .
.
(二)主要方法:
1.解决等差数列和等比数列的问题时,通常考虑两类方法:①基本量法:即运用条件转化为关于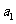 和
和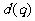 的方程;②巧妙运用等差数列和等比数列的性质,一般地运用性质可以化繁为简,减少运算量.
的方程;②巧妙运用等差数列和等比数列的性质,一般地运用性质可以化繁为简,减少运算量.
2.深刻领会两类数列的性质,弄清通项和前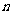 项和公式的内在联系是解题的关键.
项和公式的内在联系是解题的关键.
(一)主要知识:
有关等差、等比数列的结论
1.等差数列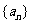 的任意连续
的任意连续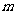 项的和构成的数列
项的和构成的数列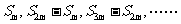 仍为等差数列.
仍为等差数列.
2.等差数列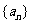 中,若
中,若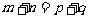 ,则
,则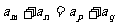
3.等比数列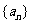 中,若
中,若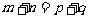 ,则
,则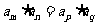
4.等比数列{an}的任意连续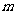 项的和构成的数列
项的和构成的数列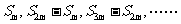 仍为等比数列.
仍为等比数列.
5.两个等差数列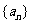 与
与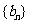 的和差的数列
的和差的数列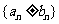 仍为等差数列.
仍为等差数列.
6.两个等比数列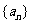 与
与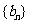 的积、商、倒数的数列
的积、商、倒数的数列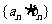 、
、 、
、 仍为等比数列.
仍为等比数列.
3.从你熟悉的树(比如松树、柳树……)中选一种,描绘它的形象,阐述它的象征意义。文辞要优美。(8分)
答:
焦作市2009-2010学年(下)《中国现代诗歌散文欣赏》水平测试
2.方文山的歌词“你发如雪,凄美了离别”中的“凄美”本来是形容词,在这里转变成动词使用。请你从熟悉的现代诗歌或歌词中再举两个词类活用的例子加以说明。(6分)
答:
1.舒婷《神女峰》中的著名诗句“与其在悬崖上展览千年/不如在爱人肩头痛哭一晚”中的“展览”能否换成“展望”?请结合全诗谈谈你的看法。(6分)
答:
14.根据下面三节诗歌的内容,填写出空缺的三句。(6分)
只要青春还在 只要生命还在
我就不会悲哀 我就不会悲哀 我就不会悲哀
纵使陷身茫茫沙漠 冬雪将会悄悄融化
太阳还可以重新回来 春雷定将滚滚而来
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com