
3.C 显然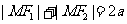 ,而
,而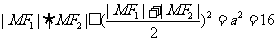 .
.
2.C 令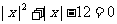 ,即
,即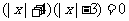 ,
,
而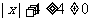 ,得
,得 ,即
,即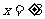 ,两交点为
,两交点为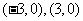 .
.
1.C 画出图形,得圆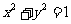 与抛物线
与抛物线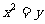 有两个交点,
有两个交点,
或观察方程组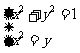 有两组解,从而得集合
有两组解,从而得集合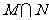 中有
中有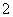 个元素.
个元素.
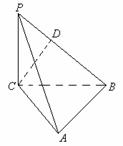
如图,在三棱锥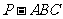 中,
中,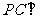 平面
平面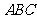 ,
,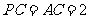 ,
,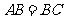 ,
,
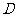 是
是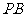 上的一点,且
上的一点,且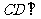 平面
平面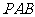 .
.
 (1)求证:
(1)求证: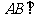 平面
平面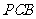 ;
;
(2)求二面角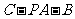 的平面角的正弦值.
的平面角的正弦值.
二○一○年军队院校招生文化科目统考
数 学 仿真模拟试卷
答案与解析
直线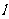 过点
过点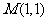 ,与椭圆
,与椭圆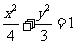 相交于
相交于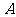 、
、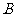 两点,若
两点,若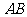 的中点为
的中点为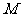 ,
,
试求直线 的方程.
的方程.
设函数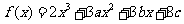 在
在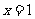 及
及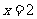 时取得极值.
时取得极值.
(1)求a、b的值;
(2)若对于任意的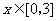 ,都有
,都有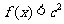 成立,求c的取值范围.
成立,求c的取值范围.
已知一口袋中有大小、质地均相同的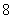 个球,其中有
个球,其中有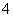 个红球和
个红球和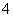 个黑球,
个黑球,
现从中任取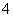 个球.
个球.
(1)求取出的球颜色相同的概率;
(2)若取出的红球数不少于黑球数,则可获得奖品,求获得奖品的概率.
数列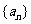 的前
的前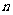 项和
项和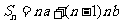 ,
,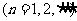 ,
,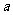 ,
,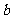 是常数,且
是常数,且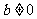 .
.
(1)证明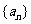 是等差数列;
是等差数列;
(2)证明以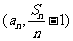 为坐标的点
为坐标的点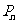 都落在同一条直线上,并求出此直线方程.
都落在同一条直线上,并求出此直线方程.
2.在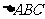 中
中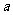 、
、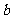 、
、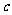 分别是角
分别是角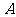 、
、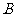 、
、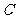 所对的边,且
所对的边,且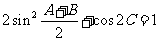 .
.
(1)求角C的大小;
(2)若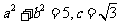 ,求
,求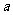 、
、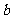 的值.
的值.
1.解下列方程: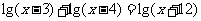 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com