
7.(安徽省合肥市2009届高三上学期第一次教学质量检测)函数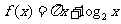 的零点所在区间为
的零点所在区间为
A.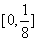 B.
B.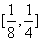 C.
C.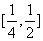 D.
D.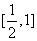
答案 C
6.(2009龙岩一中)我市某旅行社组团参加香山文化一日游,预测每天游客人数在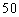 至
至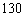 人之间,游客人数
人之间,游客人数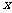 (人)与游客的消费总额
(人)与游客的消费总额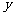 (元)之间近似地满足关系:
(元)之间近似地满足关系: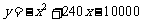 .那么游客的人均消费额最高为_________元.
.那么游客的人均消费额最高为_________元.
答案 40
5.(北京市石景山区2009年4月高三一模理)已知函数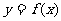 和
和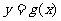 在
在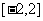 的图象如下所示:
的图象如下所示:
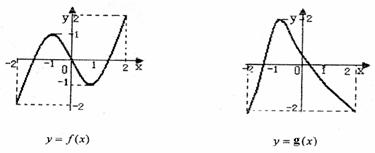
给出下列四个命题:
①方程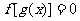 有且仅有6个根 ②方程
有且仅有6个根 ②方程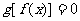 有且仅有3个根
有且仅有3个根
③方程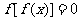 有且仅有5个根 ④方程
有且仅有5个根 ④方程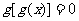 有且仅有4个根
有且仅有4个根
其中正确的命题是 .(将所有正确的命题序号填在横线上).
答案 ①③④
4.(沈阳市回民中学2008-2009学年度上学期高三第二次阶段测试文科)函数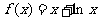 的零点所在的区间为 ( )w..A.(-1,0) B.(0,1)
的零点所在的区间为 ( )w..A.(-1,0) B.(0,1)
C.(1,2) D.(1,e)
答案 B
3.(2009莆田一中)若函数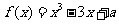 有3个不同的零点,则实数
有3个不同的零点,则实数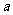 的取值范围是 ( )
的取值范围是 ( )
A.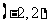 B.
B. 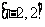 C.
C. D.
D.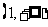
答案 A
2.(2009厦门二中)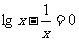 有解的区域是 ( )
有解的区域是 ( )
A.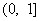 B.
B.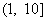 C.
C.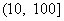 D.
D.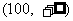
答案 B
1.(2009泉州市)函数f(x)=log2x+2x-1的零点必落在区间 ( )
A.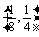 B.
B.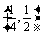 C.
C.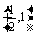 D.(1,2)
D.(1,2)
答案 C
13.(2009枣庄一模)设函数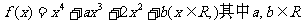
(1)当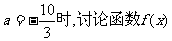 的单调性;
的单调性;
(2)若函数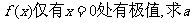 的取值范围;
的取值范围;
(3)若对于任意的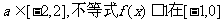 上恒成立,求
上恒成立,求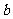 的取值范围。
的取值范围。
解:(1)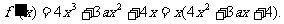
当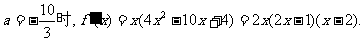
令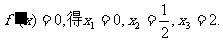
当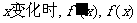 的变化情况如下表:
的变化情况如下表:
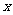 |
 |
0 |
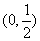 |
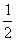 |
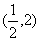 |
2 |
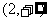 |
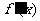 |
- |
0 |
+ |
0 |
- |
0 |
+ |
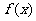 |
单调递减 |
极小值 |
单调递增 |
极大值 |
单调递减 |
极小值 |
单调递增 |
所以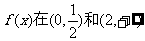 上是增函数,
上是增函数,
在区间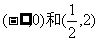 上是减函数
上是减函数
(2)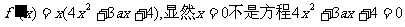 的根。
的根。
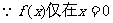 处有极值。
处有极值。
则方程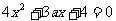 有两个相等的实根或无实根,
有两个相等的实根或无实根,

解此不等式,得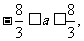
这时,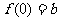 是唯一极值。
是唯一极值。
因此满足条件的
注:若未考虑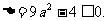 进而得到
进而得到 ,扣2分。
,扣2分。
(3)由(2)知,当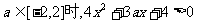 恒成立。
恒成立。
当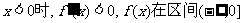 上是减函数,
上是减函数,
因此函数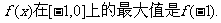 12分
12分
又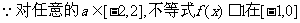 上恒成立。
上恒成立。
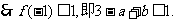
于是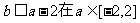 上恒成立。
上恒成立。
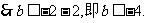
因此满足条件的
2009年联考题
12.(2009玉溪一中期末)已知函数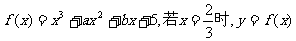 有极值,且曲线
有极值,且曲线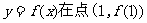 处的切线斜率为3。
处的切线斜率为3。
(Ⅰ)求函数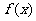 的解析式;
的解析式;
(Ⅱ)求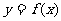 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
解:
(1)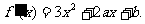 …………1分
…………1分
由题意,得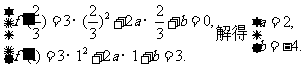 …………4分
…………4分
所以,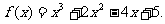 …………5分
…………5分
(2)由(1)知 ,
,
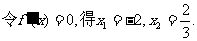 …………6分
…………6分
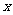 |
-4 |
(-4,-2) |
-2 |
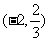 |
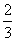 |
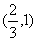 |
1 |
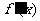 |
|
+ |
0 |
- |
0 |
+ |
|
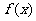 |
|
  |
极大值 |
  |
极小值 |
  |
|
|
函数值 |
-11 |
|
13 |
|
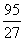 |
|
4 |
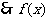 在[-4, 1]上的最大值为13,最小值为-11。 …………12分
在[-4, 1]上的最大值为13,最小值为-11。 …………12分
11.(2009日照一模)已知函数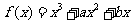 。
。
(I)若函数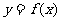 在
在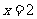 处有极值-6,求
处有极值-6,求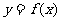 的单调递减区间;
的单调递减区间;
解:
(I)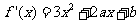
依题意有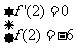
即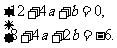 解得
解得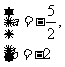
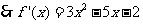
由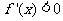 ,得
,得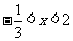
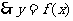 的单调递减区间是
的单调递减区间是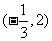
(Ⅱ)由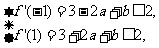 得
得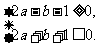
不等式组确定的平面区域如图阴影部分所示:
由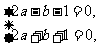 得
得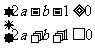
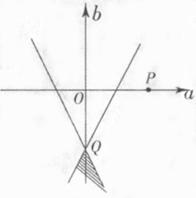 不等式组确定的平面区域如图阴影部分所示:
不等式组确定的平面区域如图阴影部分所示:
由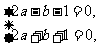 得
得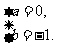
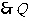 点的坐标为(0,-1).
点的坐标为(0,-1).
设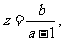 则
则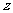 表示平面区域内的点(
表示平面区域内的点(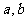 )与点
)与点
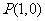 连线斜率。
连线斜率。
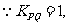 由图可知
由图可知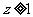 或
或 ,
,
即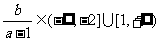
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com