
3.上表中的六个纬度,大气的削弱太阳辐射比例最大是 ( )
A. 64°N B.50°N C.0° D.20°N
读“东北地区河流封冻等日数线分布图”,回答1-2题。
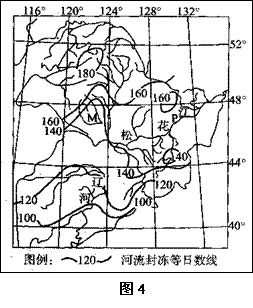
1.造成M、P两地河流封冻日数差异的主要因素是 ( )
①海拔高低 ②冬季风的影响强度 ③水流速度 ④纬度位置
A.①② B.②③ C.③④ D.①④
2.松花江防汛部门,密切注意P河段冰情,采取的合理手段是 ( )
A.利用GPS技术,分析河流未来封冻情况
B.利用GIS技术,定位冰块的流淌速度
C.利用RS技术,确定封冻河段
D.利用数字地球,虚拟河流封冻
读表2,北半球部分纬度的太阳年辐射分布,回答下列3-4题
|
纬度(°N) k*s.5.u.&com |
64 |
50 |
40 |
30 |
20 k*s.5.u.&com |
0 |
|
可能辐射量(W/m2) |
139.3 |
169.9 |
196.4 |
216.3 |
228.2 |
248.1 |
|
有效辐射量(W/m2) |
54.4 |
71.7 |
98.2 |
120.8 |
132.7 |
108.8 |
22、(本小题满分12分)
已知定点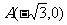 ,B是圆
,B是圆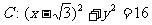 (C为圆心)上的动点,AB的垂直平分线与BC交于点E。
(C为圆心)上的动点,AB的垂直平分线与BC交于点E。
(Ⅰ)求动点E的轨迹方程;
(Ⅱ)设直线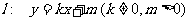 与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:
与E的轨迹交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求: OPQ面积的最大值及此时直线
OPQ面积的最大值及此时直线 的方程。
的方程。
w@w.w.k~s.5*p;m
21、(本小题满分12分)
已知函数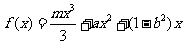 ,
,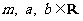 .
.
(Ⅰ)求函数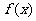 的导函数
的导函数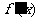 ;
;
(Ⅱ)当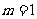 时,若函数
时,若函数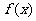 是
是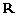 上的增函数,求
上的增函数,求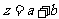 的最小值;
的最小值;
(Ⅲ)当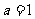 ,
,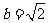 时,函数
时,函数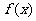 在
在 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围.
的取值范围.
w@w.w.k~s.5*p;m
20、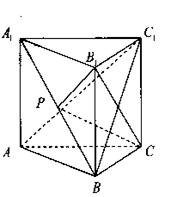 如图,三棱柱ABC-A1B1C1中,侧棱
如图,三棱柱ABC-A1B1C1中,侧棱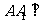 底面ABC,
底面ABC,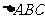 为边长为2的正三角形,点P在A1B上,且AB
为边长为2的正三角形,点P在A1B上,且AB CP。
CP。
(Ⅰ)证明:P为A1B中点;
(Ⅱ)若A1B AC1,求二面角B1-PC-B的正弦值。
AC1,求二面角B1-PC-B的正弦值。
19.(本小题满分12分)
某单位组织职工参加了旨在调查职工健康状况的测试.该测试包括心理健康测试和身体健康两个项目,每个项目的测试结果为A、B、C、D、E五个等级.假设该单位50位职工全部参加了测试,测试结果如下:x表示心理健康测试结果,y表示身体健康测试结果.
 yw@w.w.k~s.5*p;m
yw@w.w.k~s.5*p;mX |
身体健康w@w.w.k~s.5*p;m |
|||||
|
A |
B |
C |
Dw@w.w.k~s.5*p;m |
Ew@w.w.k~s.5*p;m |
||
|
心理健康 |
A |
1 |
3 |
1 |
0 |
1 |
|
B |
1 |
0 |
7 |
5 |
1 |
|
|
C |
2 |
1 |
0 |
9 |
3 |
|
|
D |
1 |
b |
6 |
0 |
a |
|
|
E |
0 |
0 |
1 |
1 |
3 |
(I)求a+b的值;
(II)如果在该单位随机找一位职工谈话,求找到的职工在这次测试中心理健康为D等且身体健康为C等的概率;
(III)若“职工的心理健康为D等”与“职工的身体健康为B等”是相互独立事件,求a、b的值.
18、(本小题满分12分w@w.w.k~s.5*p;m)
设数列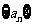 为等差数列,且
为等差数列,且 ,
,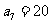 ,数列
,数列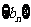 的前
的前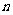 项和为
项和为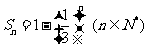 ,
,
(Ⅰ)求数列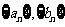 的通项公式;
的通项公式;
(Ⅱ)若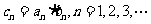 ,求数列
,求数列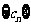 的前
的前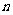 项和
项和 .
.
17、(本小题满分10分)
已知向量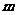
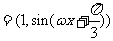 ,
,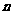
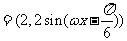 (其中
(其中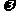 为正常数)
为正常数)
(Ⅰ)若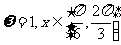 ,求
,求 时
时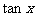 的值;
的值;
(Ⅱ)设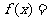
 ,若函数
,若函数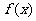 的图像的相邻两个对称中心的距离为
的图像的相邻两个对称中心的距离为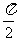 ,求
,求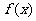 在区间
在区间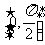 上的最小值。
上的最小值。
16、给出下列五个命题:
(1) 过平面外一点,作与该平面成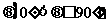 角的直线一定有无穷多条;
角的直线一定有无穷多条;
(2) 一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
(3) 对确定的两条异面直线,过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行;
(4) 对两条异面的直线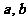 ,都存在无穷多个平面与这两条直线所成的角相等;
,都存在无穷多个平面与这两条直线所成的角相等;
(5) 直角三角形ABC中,AB=3,BC=4, AC=5,将三角形绕直角边AB旋转一周所成的几何体的体积为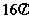 ;
;
其中正确命题的序号为 (请把所有正确命题的序号都填上)
15、双曲线的两条渐近线方程分别为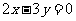 和
和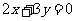 ,双曲线上的点满足不等式
,双曲线上的点满足不等式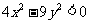 ,已知双曲线的焦距为
,已知双曲线的焦距为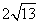 ,则双曲线方程为
,则双曲线方程为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com