
1.求圆的方程:主要用待定系数法,可以用圆的标准方程,求出圆心坐标和半径;或是利用圆的一般方程求出系数D、E、F的值。
[例1](1)求经过点A(5,2),B(3,2),圆心在直线2x─y─3=0上的圆的方程;
(2)一圆与y轴相切,圆心在直线x-3y=0上,且直线y=x截圆所得弦长为2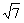 ,求此圆的方程
,求此圆的方程
解:(1)设圆心P(x0,y0),则有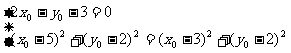 ,
,
解得 x0=4, y0=5,
∴半径r=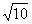 ,
,
∴所求圆的方程为(x─4)2+(y─5)2=10
(2)因圆与y轴相切,且圆心在直线x-3y=0上,
故设圆方程为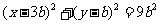

又因为直线y=x截圆得弦长为2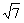 ,
,
则有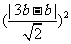 +
+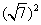 =9b2,
=9b2,
解得b=±1 故所求圆方程为
故所求圆方程为
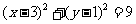 或
或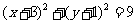

◆提炼方法:(1)确定圆方程首先明确是标准方程还是一般方程;(2)待定系数法;(3)尽量利用几何关系求a、b、r或D、E、F.
[例2]已知⊙O的半径为3,直线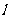 与⊙O相切,一动圆与
与⊙O相切,一动圆与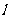 相切,并与⊙O相交的公共弦恰为⊙O的直径,求动圆圆心的轨迹方程。
相切,并与⊙O相交的公共弦恰为⊙O的直径,求动圆圆心的轨迹方程。
解:取过O点且与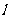 平行的直线为x轴,过O点且垂直于
平行的直线为x轴,过O点且垂直于
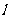 的直线为y轴,建立直角坐标系。
的直线为y轴,建立直角坐标系。
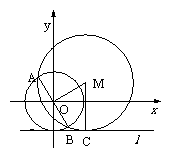 设动圆圆心为M(x,y),⊙O与⊙M的公共弦为
设动圆圆心为M(x,y),⊙O与⊙M的公共弦为
AB,⊙M与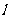 切于点C,则
切于点C,则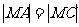
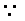 AB为⊙O的直径,
AB为⊙O的直径,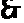 MO垂直
MO垂直
平分AB于O。
由勾股定理得
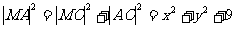
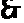
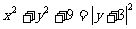
即: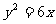 这就是动圆圆心的轨迹方程
这就是动圆圆心的轨迹方程
[例3]已知圆M:2x2+2y2-8x-8y-1=0和直线l:x+y-9=0, 过直线 上一点A作△ABC,使∠BAC=45°,AB过圆心M,且B,C在圆M上。
⑴当A的横坐标为4时,求直线AC的方程;
⑵求点A的横坐标的取值范围。
解:⑴依题意M(2,2),A(4,5),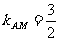 ,设直线AC的斜率为
,设直线AC的斜率为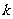 ,则
,则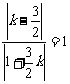 ,解得
,解得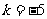 或
或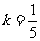 ,故所求直线AC的方程为5x+y-25=0或x-5y+21=0;
,故所求直线AC的方程为5x+y-25=0或x-5y+21=0;
⑵圆的方程可化为(x-2)2+(y-2)2=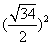 ,设A点的横坐标为a。则纵坐标为9-a;
,设A点的横坐标为a。则纵坐标为9-a;
①当a≠2时,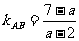 ,设AC的斜率为k,把∠BAC看作AB到AC的角,则可得
,设AC的斜率为k,把∠BAC看作AB到AC的角,则可得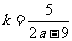 ,直线AC的方程为y-(9-a)=
,直线AC的方程为y-(9-a)=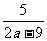 (x-a)即5x-(2a-9)y-2a2+22a-81=0,又点C在圆M上,
(x-a)即5x-(2a-9)y-2a2+22a-81=0,又点C在圆M上,
所以只需圆心到AC的距离小于等于圆的半径,
即 ,
,
化简得a2-9a+18≤0,解得3≤a≤6;
②当a=2时,则A(2,7)与直线 x=2成45°角的直线为y-7=x-2即x-y+5=0,M到它的距离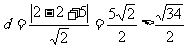 ,这样点C不在圆M上,还有x+y-9=0,显然也不满足条件,故A点的横坐标范围为[3,6]。
,这样点C不在圆M上,还有x+y-9=0,显然也不满足条件,故A点的横坐标范围为[3,6]。
[例4]设圆满足:①截y轴所得弦长为2;②被x轴分成两段圆弧,其弧长的比为3:1,在满足条件①、②的所有圆中,求圆心到直线l:x-2y=0的距离最小的圆的方程.
解法一:设圆心为P(a,b),半径为r,则点P到x轴,y轴的距离分别为│b│,│a│.
由题设圆P截x轴所得劣弧对的圆心角为900,知圆P截x轴的弦长为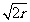 ,故r2=2b2
,故r2=2b2
又圆P截y轴所得的弦长为2,所以有r2=a2+1.从而得2b2-a2=1.
又点P(a,b)到直线x-2y=0的距离为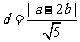
所以5d2=│a-2b│2=a2+4b2-4ab
≥a2+4b2-2(a2+b2)=2b2-a2=1,
当且仅当a=b时上式等号成立,此时5d2=1,从而d取得最小值.
由此有
解此方程组得
由于r2=2b2知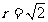 于是,所求圆的方程是:
于是,所求圆的方程是:
(x-1)2+(y-1)2=2,或(x+1)2+(y+1)2=2.
解法二:同解法一得
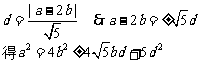
将a2=2b2-1代入上式,整理得
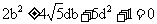 ②
②
把它看作b的二次方程,由于方程有实根,故判别式非负,即
△=8(5d2-1)≥0, 得 5d2≥1.
所以5d2有最小值1,从而d有最小值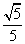
将其代入②式得2b2±4b+2=0.解得b=±1.
将b=±1代入r2=2b2,得r2=2.由r2=a2+1得a=±1.
综上 a=±1,b=±1,r2=2.
由│a-2b│=1知a,b同号.于是,所求圆的方程是
(x-1)2+(y-1)2=2,或(x+1)2+(y+1)2=2.
[研讨.欣赏]已知平面上一定点C(4,0)和一定直线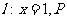 为该平面上一动点,作
为该平面上一动点,作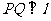 ,垂足为Q,且(
,垂足为Q,且(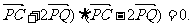
(1)问点P在什么曲线上?并求出该曲线的方程;
(2)设直线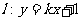 与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
解:(1)设P的坐标为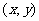 ,由
,由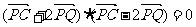 得
得
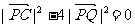
∴(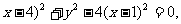 化简得
化简得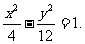
∴P点在双曲线上,其方程为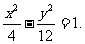
(2)设A、B点的坐标分别为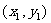 、
、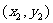 ,
,
由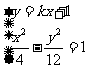 得
得
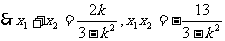 ,
,
∵AB与双曲线交于两点,∴△>0,
即 解得
解得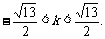
∵若以AB为直径的圆过D(0,-2),则AD⊥BD,
∴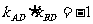 ,即
,即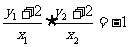
∴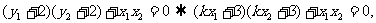
∴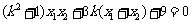
∴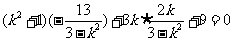 ,
, 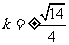
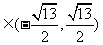
即存在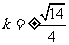 符合要求.
符合要求.
6.圆(x-2)2+(y-2)2=1关于x轴的对称方程是(x-2)2+(y+2)2=1.
设l方程为y-3=k(x+3),由于对称圆心(2,-2)到l距离为圆的半径1,从而可得k1=-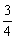 ,k2=-
,k2=-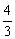 .故所求l的方程是3x+4y-3=0或4x+3y+3=0.
.故所求l的方程是3x+4y-3=0或4x+3y+3=0.
6. 自点A(-3,3)发出的光线l射到x轴上,被x轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0相切,则光线l所在直线的方程是_______________.
简答提示:1-4.BCBC; 5.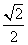
5.(2006全国Ⅱ)过点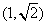 的直线
的直线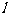 将圆
将圆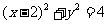 分成两段弧,当劣弧所对的圆心角最小时,直线
分成两段弧,当劣弧所对的圆心角最小时,直线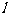 的斜率
的斜率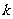 =___________.
=___________.
4.M(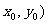 为圆
为圆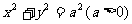 内异于圆心的一点,则直线
内异于圆心的一点,则直线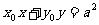 与该圆的位置关系为(
)
与该圆的位置关系为(
)
A.相切 B.相交 C.相离 D.相切或相交
3.(2005北京)从原点向圆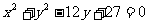 作两条切线,则该圆夹在两条切线间的劣弧长为 ( )
作两条切线,则该圆夹在两条切线间的劣弧长为 ( )
A.π B.2π C.4π D.6π
2.(2005北京)直线 所截得的线段的长为( )
所截得的线段的长为( )
A.1 B.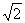 C.
C.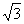 D.2
D.2
1.(2006陕西) 设直线过点(0,a),其斜率为1, 且与圆x2+y2=2相切,则a 的值为( )
A. ± B. ±2 B.±2 D.±4
9.特别提示:解直线与圆的问题,要尽量充分地利用平面几何中圆的性质,利用几何法解题要比解析方法来得简捷.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com