
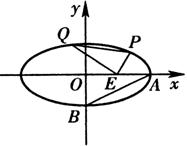
 19.(本小题满分12分)如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为
19.(本小题满分12分)如图,已知中心在原点O、焦点在x轴上的椭圆C的离心率为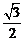 ,点A、B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为
,点A、B分别是椭圆C的长轴、短轴的端点,点O到直线AB的距离为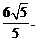 (Ⅰ)求椭圆C的方程;(Ⅱ)已知点E(3,0),设点P、Q是椭圆C上的两个动点,满足
(Ⅰ)求椭圆C的方程;(Ⅱ)已知点E(3,0),设点P、Q是椭圆C上的两个动点,满足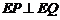 ,求
,求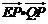 的最小值.
的最小值.
由余弦定理得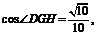 即二面角B―EF―D的大小为
即二面角B―EF―D的大小为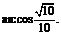

 ∴
∴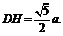 又
又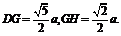 ∴在△DGH中,
∴在△DGH中,
在△BDE中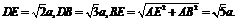 ∴
∴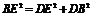 ∴
∴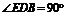 ,
,
∵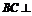 平面ACFE,∴
平面ACFE,∴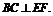 又∵
又∵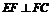 ,∴
,∴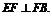 又∵
又∵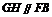 ,∴
,∴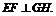 ∴
∴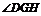 是二面角B―EF―D的平面角.
是二面角B―EF―D的平面角.
(Ⅲ)取EF中点G,EB中点H,连结DG、GH、DH,∵DE=DF,∴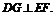
又∵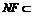 平面BDF,
平面BDF,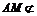 平面BDF. ∴
平面BDF. ∴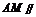 平面BDF.
平面BDF.
∴四边形ANFM是平行四边形. ∴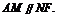
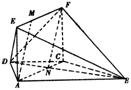 ∵
∵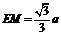 而
而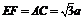 ,∴
,∴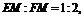 ∴MF
∴MF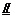 AN,
AN,
(Ⅱ)当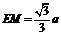 时,
时,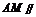 平面BDF. 在梯形ABCD中,设
平面BDF. 在梯形ABCD中,设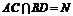 ,连结FN,则
,连结FN,则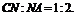
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com