
4、如果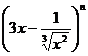 的展开式中各项系数之和为128,则展开式中的系数是( )
的展开式中各项系数之和为128,则展开式中的系数是( )
(A)7 (B)-7 (C)21 (D)-21
3、设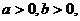 则以下不等式中不恒成立的是 ( )
则以下不等式中不恒成立的是 ( )
A.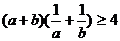 ;
B.
;
B.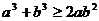 ;
;
C. ; D.
; D.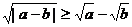
1、设复数 满足关系式
满足关系式 +│
+│ │=2+
│=2+ ,那么
,那么 等于( )
等于( )
(A) -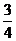 +
+ ;(B)
;(B) 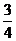 -
- ;(C) -
;(C) -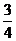 -
- ; (D)
; (D) 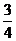 +
+ .
.
2 设函数
设函数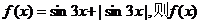 为 ( )
为 ( )
A.周期函数,最小正周期为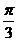 B.周期函数,最小正周期为
B.周期函数,最小正周期为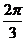
C.周期函数,数小正周期为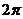 D.非周期函数
D.非周期函数
5. 已知数列{an}为等差数列,公差d≠0,{an}的部分项组成下列数列:a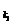 ,a
,a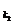 ,…,a
,…,a ,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.
,恰为等比数列,其中k1=1,k2=5,k3=17,求k1+k2+k3+…+kn.
剖析:运用等差(比)数列的定义分别求得a ,然后列方程求得kn.
,然后列方程求得kn.
解:设{an}的首项为a1,∵a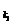 、a
、a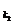 、a
、a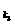 成等比数列
成等比数列
∴(a1+4d)2=a1(a1+16d)得a1=2d,q=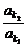 =3.
=3.
∵a =a1+(kn-1)d,又a
=a1+(kn-1)d,又a =a1·3n-1,∴kn=2·3n-1-1.
=a1·3n-1,∴kn=2·3n-1-1.
∴k1+k2+…+kn=2(1+3+…+3n-1)-n
=2×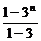 -n=3n-n-1.
-n=3n-n-1.
思悟提炼:运用等差(比)数列的定义转化为关于kn的方程是解题的关键,转化时要注意项数间的对应关系:a 是等差数列中的第kn项,而是等比数列中的第n项.
是等差数列中的第kn项,而是等比数列中的第n项.
1.若等比数列{an}的公比q<0,前n项和为Sn,则S8a9与S9a8的大小关系是
A.S8a9>S9a8 B.S8a9<S9a8 C.S8a9=S9a8 D.不确定
解析:由等比数列通项公式和前n项和公式得
S8·a9-S9·a8
=-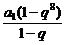 ·a1q3-
·a1q3-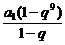 ·a1q7
·a1q7
=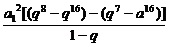 =
=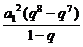 =-a12q7.
=-a12q7.
又q<0,则S8·a9-S9·a8>0,即S8·a9>S9·a8.
答案:A
3.(2006湖南)若数列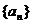 满足:
满足:  , 且对任意正整数
, 且对任意正整数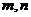 都有
都有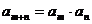 , 则
, 则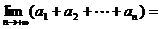 (A)
(A)
A.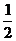 B.
B.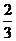 C.
C.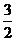 D.
D.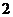
10.已知数列{an}中,a1=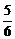 ,并且数列log2(a2-
,并且数列log2(a2-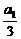 ),log2(a3-
),log2(a3-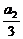 ),…,log2(an+1-
),…,log2(an+1- )是公差为-1的等差数列,求数列{an}的通项公式.
)是公差为-1的等差数列,求数列{an}的通项公式.
分析:由数列{log2(an+1- )}为等差数列及等差数列的通项公式,可求出an+1与an的一个递推关系式解:∵数列{log2(an+1-
)}为等差数列及等差数列的通项公式,可求出an+1与an的一个递推关系式解:∵数列{log2(an+1- )}是公差为-1的等差数列,
)}是公差为-1的等差数列,
∴log2(an+1- )=log2(a2-
)=log2(a2-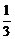 a1)+(n-1)(-1)=log2(
a1)+(n-1)(-1)=log2(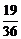 -
-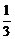 ×
×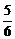 )-n+1=-(n+1),于是有an+1-
)-n+1=-(n+1),于是有an+1- =2-(n+1). 两边同乘2n+1得
=2-(n+1). 两边同乘2n+1得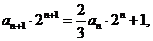
记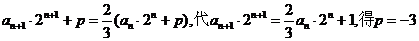
即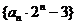 是等比数列,首项
是等比数列,首项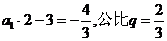
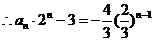 ∴an=
∴an=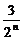 -
-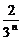 .
.
[探索题] 数列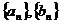 的通项公式分别是
的通项公式分别是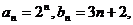 它们公共项由小到大排列的数列是
它们公共项由小到大排列的数列是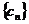 ,①写出
,①写出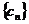 的前5项 ②证明
的前5项 ②证明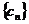 是等比数列
是等比数列
思维分析:容易证明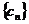 是等比数列,由定义式,只需找出
是等比数列,由定义式,只需找出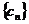 中任意相邻两项关系即可.
中任意相邻两项关系即可.
解(1) 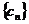 的前5项为:8、32、128、512、2048
的前5项为:8、32、128、512、2048
(2)设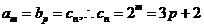 ,
,
而am+1=2·2m=2(3p+2)=3(2p+1)+1,∴am+1不在{bn}中;
又am+2=4·2m=4·(3p+2)=3·(4p+2)+2
∴am+2在{bn}中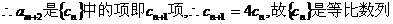
特别识记:本题是很特别的方法,与前面两个等差数列中相同的项构成的新数列的求法是不同的.应特别的记一记.
备选题
9. 设数列{an}前n的项和为 Sn,且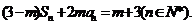 其中m为常数,
其中m为常数,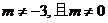
(1)求证:{an}是等比数列;
(2)若数列{an}的公比满足q=f(m)且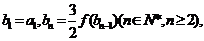
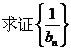 为等差数列,并求
为等差数列,并求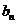
解:(1)由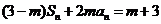 ,得
,得
两式相减,得 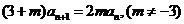

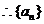 是等比数列
是等比数列
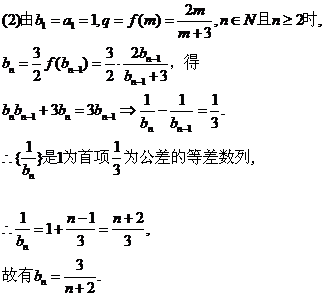
点评:为了求数列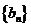 的通项,用取"倒数"的技巧,得出数列
的通项,用取"倒数"的技巧,得出数列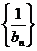 的递推公式,从而将其转化为等差数列的问题
的递推公式,从而将其转化为等差数列的问题
8.设数列{an}、{bn}(bn>0,n∈N*),满足an=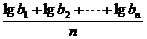 (n∈N*),证明:{an}为等差数列的充要条件是{bn}为等比数列.
(n∈N*),证明:{an}为等差数列的充要条件是{bn}为等比数列.
证明:充分性:若{bn}为等比数列,设公比为q,则an=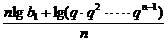 =
=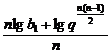 =lgb1+(n-1)lgq
=lgb1+(n-1)lgq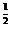 ,an+1-an=lgq
,an+1-an=lgq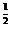 为常数,
为常数,
∴{an}为等差数列.
必要性:由an=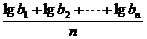 得nan=lgb1+lgb2+…+lgbn,(n+1)an+1=lgb1+lgb2+…+lgbn+1,
得nan=lgb1+lgb2+…+lgbn,(n+1)an+1=lgb1+lgb2+…+lgbn+1,
∴n(an+1-an)+an+1=lgbn+1.
若{an}为等差数列,设公差为d,
则nd+a1+nd=lgbn+1,
∴bn+1=10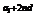 ,bn=10
,bn=10 .
.
∴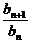 =102d为常数.
=102d为常数.
∴{bn}为等比数列.
7.数列{an}的前n项和为Sn,数列{bn}中,b1=a1,bn=an-an-1(n≥2),若an+Sn=n.
(1)设cn=an-1,求证:数列{cn}是等比数列;
(2)求数列{bn}的通项公式.
证明(1):∵a1=S1,an+Sn=n,∴a1+S1=1,得a1=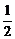 .
.
又an+1+Sn+1=n+1,两式相减得2(an+1-1)=an-1,即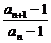 =
=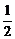 ,也即
,也即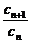 =
=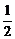 ,故数列{cn}是等比数列.
,故数列{cn}是等比数列.
(2)解:∵c1=a1-1=-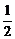 ,
,
∴cn=-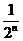 ,an=cn+1=1-
,an=cn+1=1-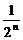 ,an-1=1-
,an-1=1-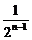 .
.
故当n≥2时,bn=an-an-1=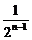 -
-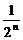 =
=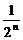 .又b1=a1=
.又b1=a1=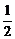 ,即bn=
,即bn=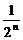 (n∈N*).
(n∈N*).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com