
6、(04年全国卷一.理2)已知函数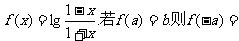
A.b B.-b C. D.-
D.-
5、 (05山东卷)下列函数既是奇函数,又在区间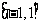 上单调递减的是
上单调递减的是
(A)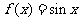 (B)
(B) (C)
(C)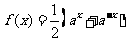 (D)
(D)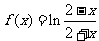
4、(05福建卷) 是定义在R上的以3为周期的偶函数,且
是定义在R上的以3为周期的偶函数,且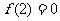 ,则方程
,则方程 =0在区间(0,6)内解的个数的最小值是
=0在区间(0,6)内解的个数的最小值是
A.5 B.4 C.3 D.2
3、已知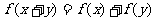 对任意实数
对任意实数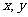 都成立,则函数
都成立,则函数 是
是
(A)奇函数 (B)偶函数
(C)可以是奇函数也可以是偶函数 (D)不能判定奇偶性
2、已知 是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则
是定义在R上的奇函数,且为周期函数,若它的最小正周期为T,则
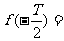
(A)0 (B)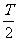 (C)
(C)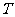 (D)
(D)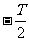
1、若
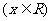 是奇函数,则下列各点中,在曲线
是奇函数,则下列各点中,在曲线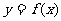 上的点是
上的点是
(A)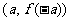 (B)
(B)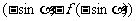 (C)
(C)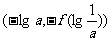 (D)
(D)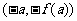
10.甲、乙两地相距Skm,汽车从甲地匀速行驶到乙地,速度不得超过c km/h,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度v(km/h)的平方成正比,比例系数为b;固定部分为a元.
(1)把全程运输成本y(元)表示为速度v(km/h)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶.
分析:(1)抓住关系式:全程运输成本=单位时间运输成本×全程运输时间,而全程运输时间=(全程距离)÷(平均速度)就可以解决.
解(1)由已知汽车从甲地到乙地所用时间为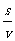 ,全程运输成本为
,全程运输成本为
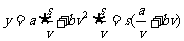
∴所求函数及定义域为: 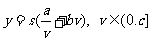
(2)依题意S,a,b,v都是正数,故有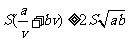
当且仅当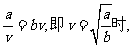 上式等号成立.
上式等号成立.
若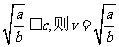 时,全程运输成本最小.
时,全程运输成本最小.
若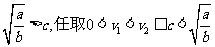 ,则
,则
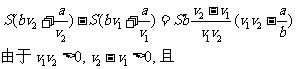

∴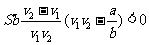 即
即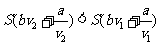
∴当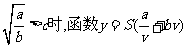 在区间(0,c]上是减函数.
在区间(0,c]上是减函数.
则当v=c时,y取最小值.
综上可知,当 时,速度应为
时,速度应为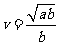 ;当
;当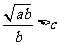 时,速度应为v=c;
时,速度应为v=c;
说明:此题是1997年全国高考试题.由于限制汽车行驶速度不得超过c,因而求最值的方法也就不完全是常用的方法,再加上字母的抽象性,使难度有所增大.
[探索题]某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品.根据经验知道,该厂生产这种仪器,次品率 与日产量
与日产量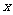 (件)之间大体满足关系:
(件)之间大体满足关系:
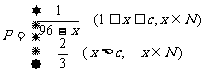 (其中c为小于96的正常数)
(其中c为小于96的正常数)
注:次品率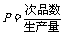 ,如
,如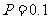 表示每生产10件产品,约有1件为次品.其余为合格品.
表示每生产10件产品,约有1件为次品.其余为合格品.
已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损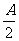 元,故厂方希望定出合适的日产量.
元,故厂方希望定出合适的日产量.
(1)试将生产这种仪器每天的盈利额 (元)表示为日产量
(元)表示为日产量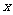 (件)的函数;
(件)的函数;
(2)当日产量为多少时,可获得最大利润?
解:(1)当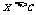 时,
时,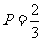 ,所以,每天的盈利额
,所以,每天的盈利额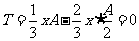 ;
;
当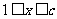 时,
时,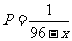 ,
,
所以,每日生产的合格仪器约有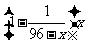 件,次品约有
件,次品约有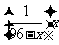 件.故,每天的盈利额
件.故,每天的盈利额
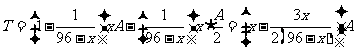

综上,日盈利额 (元)与日产量
(元)与日产量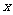 (件)的函数关系为:
(件)的函数关系为:
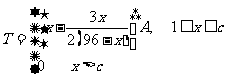
(2)由(1)知,当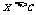 时,每天的盈利额为0.
时,每天的盈利额为0.
当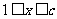 时,
时,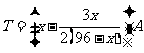 .
.
令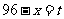 ,则
,则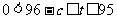 .
.
故 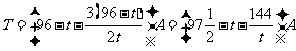
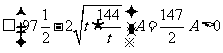 .
.
当且仅当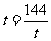 ,即
,即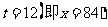 时,等号成立.
时,等号成立.
所以(i)当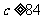 时,
时,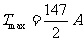 (等号当且仅当
(等号当且仅当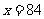 时成立).
时成立).
(ii) 当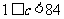 时,由
时,由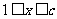 得
得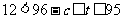 ,
,
易证函数T(t)在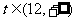 上单调递减(证明过程略).
上单调递减(证明过程略).
∴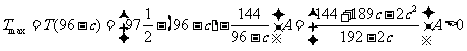 即
即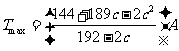 .(等号当且仅当t=96-c即
.(等号当且仅当t=96-c即 时取得)
时取得)
综上,若 ,则当日产量为84件时,可获得最大利润;若
,则当日产量为84件时,可获得最大利润;若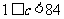 ,则当日产量为
,则当日产量为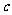 时,可获得最大利润.
点评 分段函数是历年高考的热门话题,常考常新,值得我们在复课时认真对待.
时,可获得最大利润.
点评 分段函数是历年高考的热门话题,常考常新,值得我们在复课时认真对待.
9.某影院共有1000个座位,票价不分等次。根据该影院的经营经验,当每张标价不超过10元时,票可全部售出,当每张票价高于10元时,每提高1元,将有30张票不能售出,为了获得更好的收益,需给影院一个合适的票价,符合的基本条件是:①为方便找零和算帐,票价定为1元的整数倍;②影院放映一场电影的成本费用支出为5750元,票房收入必须高于成本支出。用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入)。
(1)把y表示成x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,每张票价定为多少元时,放映一场的净收入最多?
解:(1)由题意知当x≤10时,y=1000x-5750,
当x>10时,y=[1000-30(x-10)]x-5750= -30x2+1300x-5750

又x∈N,∴6≤x≤38 ∴所求表达式为

(2)当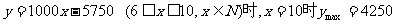
当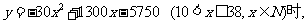
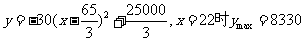
所以每张票价定为22元时净收入最多。
8.某市有小灵通与全球通两种手机,小灵通手机的月租费为25元,接听电话不收费,打出电话一次在3 min以内收费0.2元,超过3 min的部分为每分钟收费0.1元,不足1 min按1 min计算(以下同).全球通手机月租费为10元,接听与打出的费用都是每分钟0.2元.若某人打出与接听次数一样多,每次接听与打出的时间在1 min以内、1到2 min以内、2到3 min以内、3到4 min以内的次数之比为4∶3∶1∶1.问,根据他的通话次数应该选择什么样的手机才能使费用最省?(注:m到m+1 min以内指含m min,而不含m+1 min)
解:设小灵通每月的费用为y1元,全球通的费用为y2元,分别在1 min以内、2 min以内、3 min以内、4 min以内的通话次数为4x、3x、x、x,则
y1=25+(4x+3x+x+x)×0.2+0.1x=25+1.9x,
y2=10+2(0.2×4x+0.4×3x+0.6x+0.8x)=10+6.8x.
令y1≥y2,即25+1.9x≥10+6.8x,
解得x≤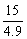 ≈3.06.
≈3.06.
∴总次数为(4+3+1+1)×2×3.06=55.1.
故当他每月的通话次数小于等于55次时,应选择全球通,大于55次时应选择小灵通.
7.设m是实数,记M={m|m>1},f(x)=log3(x2-4mx+4m2+m+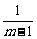 )
)
(1)证明:当m∈M时,f(x)对所有实数都有意义;反之,若f(x)对所有实数x都有意义,则m∈M
(2)当m∈M时,求函数f(x)的最小值
(3)求证:对每个m∈M,函数f(x)的最小值都不小于1
(1)证明:先将f(x)变形:f(x)=log3[(x-2m)2+m+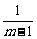 ],
],
当m∈M时,m>1,∴(x-m)2+m+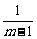 >0恒成立,
>0恒成立,
故f(x)的定义域为R
反之,若f(x)对所有实数x都有意义,则只须x2-4mx+4m2+m+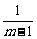 >0,
>0,
令Δ<0,即16m2-4(4m2+m+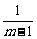 )<0,解得m>1,故m∈M
)<0,解得m>1,故m∈M
(2)解析:设u=x2-4mx+4m2+m+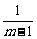 ,
,
∵y=log3u是增函数,∴当u最小时,f(x)最小?
而u=(x-2m)2+m+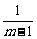 ,
,
显然,当x=m时,u取最小值为m+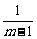 ,
,
此时f(2m)=log3(m+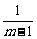 )为最小值
)为最小值
(3)证明:当m∈M时,m+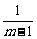 =(m-1)+
=(m-1)+ 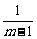 +1≥3,
+1≥3,
当且仅当m=2时等号成立.
∴log3(m+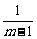 )≥log33=1
)≥log33=1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com